
Лекции Гирдрогазодинамика / 18,19
.doc18.Характеристики в плоском сверхзвуковом потоке. Общие свойства характеристик. Дифференциальные уравнения характеристик в физической плоскости.
Рассмотрим плоский стационарный безвихревой сверхзвуковой поток идеального невязкого газа. В декартовой системе координат х, у поле скоростей течения записывается в векторном виде V=V(x,y) или для составляющих скорости по осям х и у как U=U(x,y), V=V(x,y).
Характеристиками называются линии, исходящие из действительного или виртуального источника слабых возмущений в сверхзвуковом потоке газа и являющиеся границами области распространения этих возмущений; они известны также под названиями линий Маха или слабых волн.
Как
следует из рассмотренного выше (см.п.11).
в однородном сверхзвуковом потоке
слабые возмущения, исходящие из точки
О- источника возмущений, - при своем
распространении не выходят за границы
угла, образованного лучами ОА1
и ОА2,
наклон которых к направлению скорости
V
составляет
![]() ,
где
,
где
![]() =
=![]() arcsin
(1\M)
(18/1) угол Маха, М=V/а – число Маха. Переходя
к неоднородному сверхзвуковому потоку,
отсюда можно заключить, что в каждой
точке определяются два характеристических
направления, в общем случае меняющиеся
при переходе от одной точки к другой,
которые наклонены к вектору местной
скорости под углами
arcsin
(1\M)
(18/1) угол Маха, М=V/а – число Маха. Переходя
к неоднородному сверхзвуковому потоку,
отсюда можно заключить, что в каждой
точке определяются два характеристических
направления, в общем случае меняющиеся
при переходе от одной точки к другой,
которые наклонены к вектору местной
скорости под углами![]()
![]() ,
таким образом могут быть определены
два семейства характеристик как линий
(кривых), касательных в каждой точке
которых имеют то или иное характеристическое
направление (рис.?)
,
таким образом могут быть определены
два семейства характеристик как линий
(кривых), касательных в каждой точке
которых имеют то или иное характеристическое
направление (рис.?)
Все изложенное выше позволяет сформировать следующие общие свойства характеристик в физической плоскости:
1.Через
каждую точку плоскости сверхзвукового
течения газа проходят две характеристики,
принадлежащие к разным семействам,
которые в каждой своей точке образуют
с вектором скорости V
углы +![]() ,
где
,
где
![]() -угол
Маха ( sin
-угол
Маха ( sin![]() =
=
![]() ).
).
2.Вектор скорости V направлен по биссектрисе угла между характеристиками, принадлежащими к разным семействам.
3.Проекции вектора скорости V на нормали к характеристикам в данной точке Vn,1 и Vn,2 равны по абсолютной величине местной скорости звука а. Это следует из рассмотрения прямоугольного треугольника ОА1О1 (рис.?), образованного вектором скорости V=ОО1, касательной к характеристике в точке О - ОА1 и нормалью О1А1, опущенной из точки О1 на касательную:
Vn,1=
О1А1=
ОО1sin![]() =V
=V![]() =a;
=a;
аналогично
Vn,2=a.
Добавим, что при V=a(M=1)
![]() =
=![]() и характеристики обоих семейств сливаются
в одну линию, перпендикулярную к
направлению к направлению скорости
потока.
и характеристики обоих семейств сливаются
в одну линию, перпендикулярную к
направлению к направлению скорости
потока.
Выражая
в физической плоскости течения
характеристические линии 1-го и 2-го
семейств равенствами Y=Y1(x)
и Y=Y2(x),
получим дифференциальные уравнения
характеристик в указанной плоскости.
Обозначив
![]() 1
и
1
и
![]() 2
углы наклона этих линий к оси х,
2
углы наклона этих линий к оси х,
![]() -угол
наклона скорости V
к оси х, из геометрических соображений
будем иметь (см. рис.?)
-угол
наклона скорости V
к оси х, из геометрических соображений
будем иметь (см. рис.?)
![]()
![]() 1,
1,
![]()
![]() 2,
2,
tg![]() =
=![]() ,
,
![]() 1=
1=![]() +
+![]() ,
,
![]() 2=
2=![]() -
-![]()
Из
определения угла маха
![]() (18.1)
имеем
(18.1)
имеем
tg![]() =
=![]() .
.
Из
(18.2) и (18.4) следует, что
![]()
Подставляя сюда (18.3) и (18.5), после простых преобразований получим
![]() =
=![]()
Эти
дифференциальные уравнения характеристик
двух семейств действительны при условии
V![]() (или
М
(или
М![]() ),
т.е. что поток сверхзвуковой. Они могут
быть проинтегрированы, если известно
поле скоростей V=V(x,y);
скорость звука а при этом легко
определяется из уравнения энергии в
форме (12.3 или 12.6) тоже как a=a(x,y).
При V=а
уравнение (18.6) имеет только один корень,
т.е. обе характеристики как бы сливаются
в одну линию, перпендикулярную к линии
тока. Для дозвукового течения V<a
и уравнение 18.6 не имеет вещественных
корней, т.е. и действительных характеристик
не существует.
),
т.е. что поток сверхзвуковой. Они могут
быть проинтегрированы, если известно
поле скоростей V=V(x,y);
скорость звука а при этом легко
определяется из уравнения энергии в
форме (12.3 или 12.6) тоже как a=a(x,y).
При V=а
уравнение (18.6) имеет только один корень,
т.е. обе характеристики как бы сливаются
в одну линию, перпендикулярную к линии
тока. Для дозвукового течения V<a
и уравнение 18.6 не имеет вещественных
корней, т.е. и действительных характеристик
не существует.
19.Характеристики в плоскости годографа скорости. Диаграмма характеристик
Физическую
плоскость мы рассматриваем здесь как
плоскость переменных х и у – декартовых
координат, определяющих положение
произвольной точки о этой плоскости.
Течение жидкости определяет вектор
скорости V
в произвольной точке области течения,
этому вектору соответствует точка О1
– конец вектора скорости V=ОО1
(рис ?) – и две составляющие этого вектора
по осям х и у - u
и
![]() .
Эти величины можно рассматривать как
декартовы координаты точки О1
в так называемой плоскости годографа
скорости, т.е. плоскости переменных u
и
.
Эти величины можно рассматривать как
декартовы координаты точки О1
в так называемой плоскости годографа
скорости, т.е. плоскости переменных u
и
![]() .
Таким образом, каждой точке О(х, у) области
течения соответствует точка О1(u,
.
Таким образом, каждой точке О(х, у) области
течения соответствует точка О1(u,![]() )
плоскости годографа. Указанное
соответствие можно распространить на
любые линии в области течения, принадлежащей
физической плоскости (х, у), и в плоскости
годографа (u,
)
плоскости годографа. Указанное
соответствие можно распространить на
любые линии в области течения, принадлежащей
физической плоскости (х, у), и в плоскости
годографа (u,![]() ).
В частности, характеристикам в физической
плоскости будут соответствовать
характеристики в плоскости годографа.
).
В частности, характеристикам в физической
плоскости будут соответствовать
характеристики в плоскости годографа.
Исследование дифференциальных уравнений в частных производных, описывающих плоские безвихревые течения идеального газа, показывает, что имеет место следующая связь между направлениями характеристик в физической плоскости и плоскости годографа: при выборе координат осей и параллельными осям х и у характеристические направления первого семейства в физической плоскости будут перпендикулярны к характеристическим направлениям 2-го семейства в соответствующей точке плоскости годографа и , наоборот, характеристические направления второго семейства в физической плоскости перпендикулярны к характеристическим направлениям первого семейства в плоскости годографа. Т.е., если обозначить коэффициенты наклона соответствующих характеристик как
![]() =m1,2,
=m1,2,
![]() =n1,2,
=n1,2,
то m1n2=-1, m2n1=-1.
Это свойство называется сопряженностью характеристик в физической плоскости и плоскости годографа скорости.
Из свойства сопряженности (19.1) и уравнений (18.6) легко получаются следующие дифференциальные уравнения характеристик в плоскости годографа:
![]() =
=![]() .
.
Перейдем
здесь от проекций скорости u
и
![]() к модулю скорости V
и углу ее наклона к оси х -
к модулю скорости V
и углу ее наклона к оси х -
![]() ,
положив U=Vcos
,
положив U=Vcos![]() ,
,
![]() ;
;
du=cos![]() d
d![]()
Тогда уравнение (19.2) перейдет в следующее:
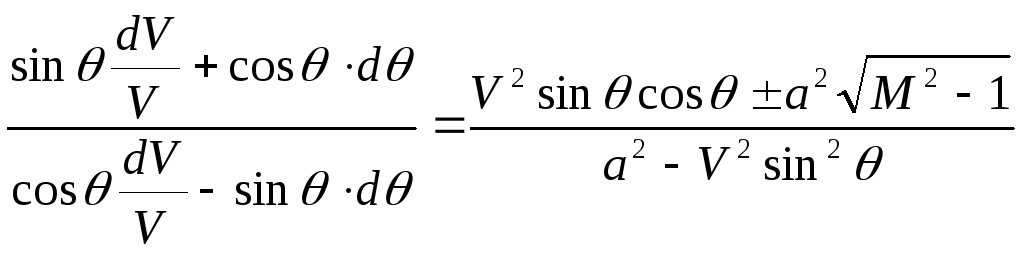 .
.
Собирая
здесь члены с
![]() и
и
![]() и затем разделяя переменные, после
преобразования найдем
и затем разделяя переменные, после
преобразования найдем
![]() =
=![]()
![]()
![]() .
.
Перейдем здесь от числа М к приведенной скорости согласно (12.7) и получим следующее дифференциальное уравнение:
![]() =
=![]()
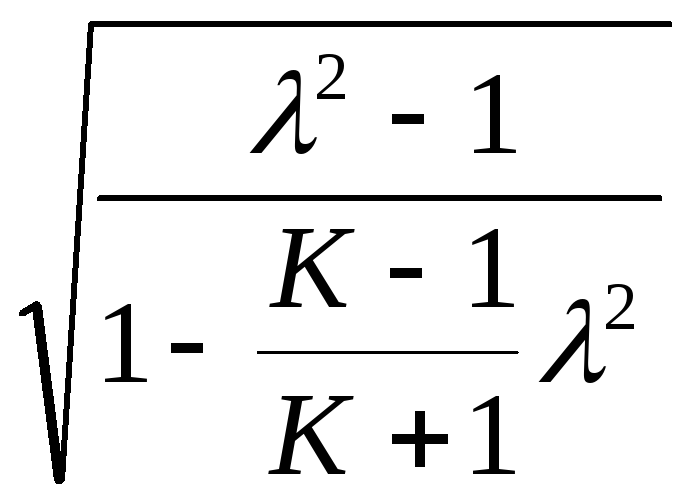
![]() .
.
Существенно, что это уравнение может быть проинтегрировано замкнутой форме и позволяет получить конечные уравнения характеристик в плоскости годографа, а именно:
![]() =
=![]() или
или
![]() ,
,
![]() =
=![]()
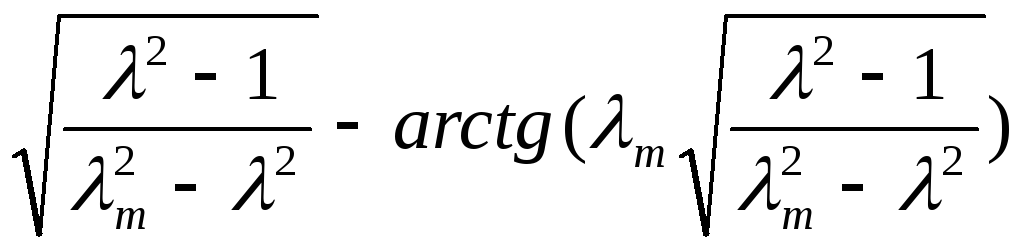
![]() (M)=
(M)=![]() ,
,
где
![]()
![]() (12.8),
(12.8),
![]() и
и
![]() – постоянные интегрирования.
– постоянные интегрирования.
Отметим,
что функции
![]() и
и
![]() монотонно
возрастающие, их значения при 1
монотонно
возрастающие, их значения при 1![]() ,
,1
,
,1![]() M<
M<![]() меняются в пределах 0
меняются в пределах 0![]() ,
где
,
где
![]() =
=![]() .
.
Итак,
вдоль характеристик изменение угла
наклона скорости
![]() определенным образом связано с
изменением модуля скорости V.
Эта связь не зависит от условий конкретной
задачи, т.е. она универсальна и выражается
уравнениями (19.4) и (19.5). При изменении
приведенной скорости от
определенным образом связано с
изменением модуля скорости V.
Эта связь не зависит от условий конкретной
задачи, т.е. она универсальна и выражается
уравнениями (19.4) и (19.5). При изменении
приведенной скорости от
![]() до
до
![]() соответственно – числа Маха – от М' до
М'' угол поворота потока вдоль характеристики
равен
соответственно – числа Маха – от М' до
М'' угол поворота потока вдоль характеристики
равен
![]()
Наибольший
возможный угол поворота получается при
![]() =1,
и равен
=1,
и равен
![]() =
=![]() и
равен
и
равен
![]() ;
например, при к=1.4
;
например, при к=1.4
![]()
![]() 0.725
0.725![]()
![]() 130.5
130.5![]() .
.
![]() и
и
![]() )
)
Для удобства численных расчетов зависимости и (19.5) и (19.5) протабулированы и включены в таблицы газодинамических функций.
Если
в плоскости годографа приведенной
скорости использовать полярную систему
координат (![]() ),
то кривые, соответствующие уравнениям
(19.4), (19.5), будут заключеныв кольце между
окружностями
),
то кривые, соответствующие уравнениям
(19.4), (19.5), будут заключеныв кольце между
окружностями
![]() =1 и
=1 и
![]() =
=![]() и
представляют собой два семейства
эпициклоид – кривых, описываемых точками
окружностями радиуса r=
и
представляют собой два семейства
эпициклоид – кривых, описываемых точками
окружностями радиуса r=![]() ,
катящейся по кругу
,
катящейся по кругу
![]() =1
в обоих возможных направлениях (рис.?).
=1
в обоих возможных направлениях (рис.?).
Для
каждого значения параметра k
в плоскости годографа может быть
построена сетка (диаграмма) эпициклоид
обоих семейств, получающихся из уравнений
(19.4), (19.5) при различных начальных углах
![]() и
и
![]() .
эта сетка называется диаграммой
характеристик и используется при
графических способах определения
скоростей сверхзвуковых течений газа.
.
эта сетка называется диаграммой
характеристик и используется при
графических способах определения
скоростей сверхзвуковых течений газа.
