
- •Тема 1. Дифференциалы и элементарное интегрирование
- •Интегрирование заменой переменной и интегрирование по частям
- •Интегрирование рациональных дробей
- •4. Интегрирование иррациональностей
- •Интегрирование тригонометрических функций
- •Определенный интеграл
- •Приложения определенного интеграла
- •Числовые ряды
- •9. Степенные ряды
- •Список рекомендуемой литературы
Интегрирование заменой переменной и интегрирование по частям
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Для
вычисления данного интеграла сделаем
замену:
![]() .
Тогда
.
Тогда![]() ,
,![]() .
Исходный интеграл сведется к виду:
.
Исходный интеграл сведется к виду:
![]()
Чтобы вычислить полученный интеграл, раскроем в числителе куб разности и почленно разделим числитель на знаменатель. Имеем:
![]()
Каждое
из слагаемых под знаком интеграла
представляет собой степенную функцию.
Почленно интегрируем выражение и затем
возвращаемся к исходной переменной
![]() :
:
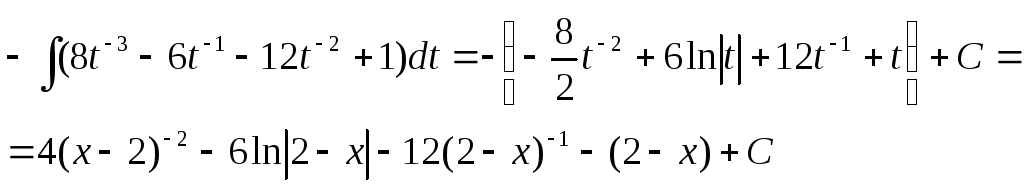
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Сделаем
замену:
![]() .
Тогда
.
Тогда![]() .
Видно, что синус, стоящий в подинтегральной
функции, войдет в дифференциал
.
Видно, что синус, стоящий в подинтегральной
функции, войдет в дифференциал![]() .
Тогда
.
Тогда
![]() .
.
Следует
отметить, что в данном случае замена
![]() эквивалентна внесению
эквивалентна внесению![]() под
знак дифференциала:
под
знак дифференциала:
![]() .
.
Тогда интегрируя, получим тот же самый результат:
![]() .
.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Представим подинтегральную функцию в виде:
![]()
Теперь можно внести cos x под знак дифференциала, или сделать замену:
![]()
Тогда косинус, стоящий в числителе, войдет в дифференциал новой переменной t:
![]() .
.
Чтобы привести этот интеграл к табличному интегралу вида
![]() ,
,
нужно вынести из знаменателя знак минус:
![]() .
.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Данный интеграл можно преобразовать к табличному, если за новую переменную обозначить подкоренное выражение:

5.
Вычислить интеграл:
![]() .
.
РЕШЕНИЕ:
Вносим
множитель
![]() под
знак дифференциала:
под
знак дифференциала:
![]() .
.
(Это
эквивалентно замене переменной:
![]() ).
Тогда интеграл сведется к табличному
интегралу
).
Тогда интеграл сведется к табличному
интегралу
![]()
Имеем:
![]()
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Применим метод интегрирования по частям, который описывается формулой:
![]()
Выберем
![]()
Тогда
![]()
Подставляем в формулу интегрирования по частям:
![]()
7.
Вычислить интеграл:
![]() .
.
РЕШЕНИЕ:
Снова интегрируем по частям:

(Последний интеграл взяли с помощью замены переменной).
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Интегрируем по частям:

Полученный
интеграл, в отличие от исходного, содержит
![]() в
первой степени, поэтому видно, что
проинтегрировав его еще раз по частям,
мы в итоге получим интеграл, содержащий
только тригонометрическую функцию:
в
первой степени, поэтому видно, что
проинтегрировав его еще раз по частям,
мы в итоге получим интеграл, содержащий
только тригонометрическую функцию:
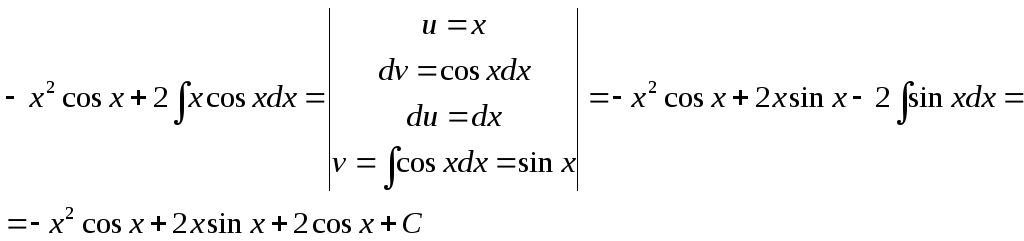
Отметим, что метод интегрирования по частям удобно применять к интегралам следующих основных типов:
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
2.1. Вычислить интегралы, используя замену переменной:
а)![]() б)
б)![]() в)
в)![]() г)
г)![]() д)
д)![]() е)
е)![]()
ж)![]() з)
з)![]() и)
и)![]() к)
к)![]() л)
л)![]()
м)![]() н)
н)![]() о)
о)![]() п)
п)![]() р)
р)![]()
с)
![]() т)
т)![]() у)
у)![]() ф)
ф)![]() х)
х)![]()
2.2. Вычислить интегралы методом интегрирования по частям:
а)![]() б)
б)![]() в)
в)![]() г)
г)![]() д)
д)![]() е)
е)![]()
ж)![]() з)
з)![]() и)
и)![]() к)
к)![]() л)
л)![]()
м)
![]() н)
н)![]() о)
о)![]()
Интегрирование рациональных дробей
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Вычислить интеграл

РЕШЕНИЕ:
В
знаменателе дроби квадратный трехчлен:
![]() .
.
Выделим в знаменателе полный квадрат:
![]()
Тогда выражение, стоящее в квадрате, можно обозначить за новую переменную (интеграл при этом сведется к табличному):
![]()
Этот
результат можно получить из других
соображений. Поскольку к переменной
под дифференциалом можно без изменения
его значения прибавлять или вычитать
любое число, положим
![]() .
Интеграл при этом сведется к табличному:
.
Интеграл при этом сведется к табличному:
![]()
Вычислить интеграл:

РЕШЕНИЕ:
.
Снова выделяем в знаменателе полный квадрат и преобразуем выражение под дифференциалом:
![]()
![]()
Полученный интеграл еще не является табличным. Чтобы привести его к табличному виду, надо вынести из знаменателя знак минус:
Имеем:
![]()
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Выделяем в знаменателе полный квадрат и делаем замену:
![]()
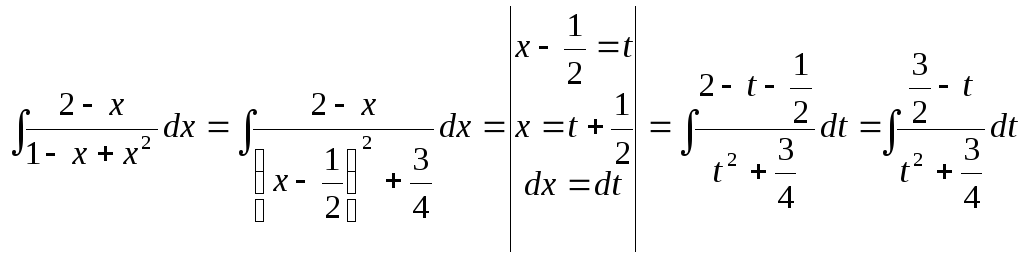
Полученный интеграл еще не является табличным. Делим числитель почленно на знаменатель и разбиваем исходный интеграл на разность двух интегралов:

Первый
интеграл табличный. Второй интеграл
берется заменой
![]() .
Тогда
.
Тогда![]() .
Эта замена эквивалентна внесению
.
Эта замена эквивалентна внесению![]() под знак дифференциала. Имеем:
под знак дифференциала. Имеем:

Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Выделяем в знаменателе полный квадрат и делаем замену:
![]()

Снова
разбиваем на два интеграла. Первый
интеграл табличный. Второй берем заменой
![]() .
Тогда
.
Тогда![]() .
Получим:
.
Получим:
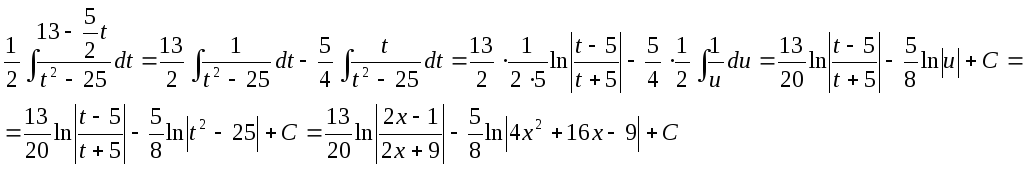
5.
Вычислить интеграл:
![]()
РЕШЕНИЕ:
Для вычисления этого интеграла применим метод неопределенных коэффициентов. Подинтегральную дробь разложим на сумму элементарных дробей:
![]() .
.
Чтобы
определить коэффициенты
![]() ,
приведем дроби в правой части к общему
знаменателю:
,
приведем дроби в правой части к общему
знаменателю:
![]()
Приравняем числители полученной и исходной дробей:
![]()
Приравнивая
коэффициенты при одинаковых степенях
![]() ,
можно найти искомые коэффициенты.
Поскольку данное равенство справедливо
для любых значенияхх,
то полагая x
равным поочередно значениям, обращающим
в нуль знаменатель( то есть 1, -3 и 4)
последовательно найдем все неопределенные
коэффициенты.
,
можно найти искомые коэффициенты.
Поскольку данное равенство справедливо
для любых значенияхх,
то полагая x
равным поочередно значениям, обращающим
в нуль знаменатель( то есть 1, -3 и 4)
последовательно найдем все неопределенные
коэффициенты.
![]()
Тогда
подставляем в исходное выражение
![]() :
:
![]()
Слагаемые с коэффициентами А и С обращаются в ноль и остается
![]()
Аналогично, если
![]()
![]()
![]()
И в последнем случае
![]()
![]()
![]()
Теперь подставляем найденные коэффициенты в разложение, и исходный интеграл представляем в виде суммы трех интегралов, каждый из которых будет табличным:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Вычислить интегралы с помощью замены переменной:
а)![]() ;б)
;б)![]() в)
в)![]() г)
г)![]()
д)![]() е)
е)![]() ж)
ж)![]() з)
з)![]()
и)![]() к)
к)![]() л)
л)![]()
3.2. Вычислить интегралы методом неопределенных коэффициентов:
а)![]() б)
б)![]() в)
в)![]() г)
г)![]()
д)![]() е)
е)![]() ж)
ж)![]() з)
з)![]()
и)![]()
