
- •Тема 1. Дифференциалы и элементарное интегрирование
- •Интегрирование заменой переменной и интегрирование по частям
- •Интегрирование рациональных дробей
- •4. Интегрирование иррациональностей
- •Интегрирование тригонометрических функций
- •Определенный интеграл
- •Приложения определенного интеграла
- •Числовые ряды
- •9. Степенные ряды
- •Список рекомендуемой литературы
Определенный интеграл
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Для вычисления определенного интеграла используем формулу Ньютона-Лейбница:
![]()
Сначала находим первообразную для подинтегральной функции:
![]() .
.
Так
как в формуле Ньютона-Лейбница можно
использовать любую первообразную, то
возьмем такую первообразную, для которой
![]() .
.
Получим:
 .
.
Заметим, что сначала в первообразную подставляется верхний предел интегрирования а затем нижний. В отличие от неопределенного интеграла, при вычислении которого получается семейство функций, определенный интеграл равен конкретному числу.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
По формуле Ньютона-Лейбница:

Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Используем
замену переменной:
![]() .
Тогда
.
Тогда![]() .
Один из синусов войдет в дифференциал.
Останется
.
Один из синусов войдет в дифференциал.
Останется![]() .
Меняем пределы интегрирования: на нижнем
пределе
.
Меняем пределы интегрирования: на нижнем
пределе![]() ,
следовательно
,
следовательно![]() .
Верхний предел:
.
Верхний предел:![]() .
.
Имеем:

По свойству определенного интеграла, можно поменять местами пределы интегрирования (это делается для удобства вычислений, чтобы нижний предел был меньше верхнего), при этом поменяется знак перед интегралом:

Заметим, что при использовании замены переменной в определенном интеграле ненужно возвращаться к старой переменной, как это делалось при вычислении неопределенных интегралов, поскольку одновременно с заменой переменной мы меняем пределы интегрирования.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Снова используем замену переменной в определенном интеграле:

5.
Вычислить интеграл:
 .
.
РЕШЕНИЕ:
Используем метод интегрирования по частям:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Вычислить определенный интеграл:
а) б)
б)![]() в)
в)![]() г)
г)![]()
д) е)
е) ж)
ж)![]() з)
з) и)
и)![]()
Вычислить определенный интеграл, используя замену переменной:
а)![]() б)
б)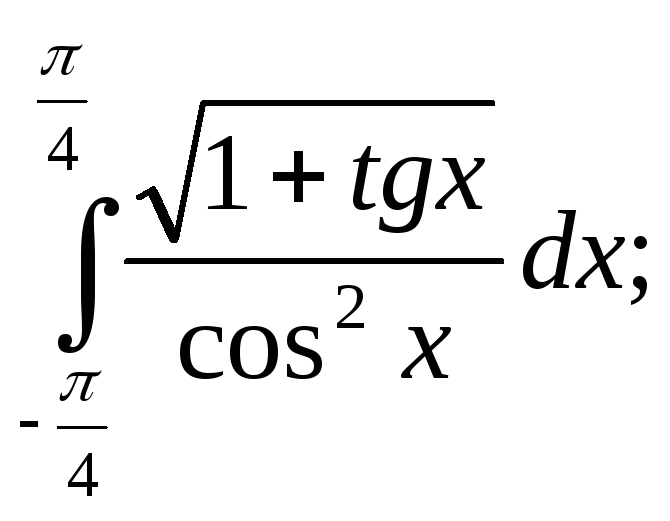 в)
в)![]() г)
г)![]() д)
д)![]()
е)![]() ж)
ж) з)
з)![]() и)
и)![]() к)
к)
Вычислить определенный интеграл, используя интегрирование по частям:
а)
 б)
б)![]() в)
в)![]() г)
г) д)
д)![]()
е)![]() ж)
ж)![]() з)
з)![]()
Приложения определенного интеграла
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Найти площадь фигуры, ограниченной линиями:
 и
и .
.
РЕШЕНИЕ:
Первая линия представляет собой параболу с вершиной в точке (0;4) и ветвями, направленными вниз. Вторая линия тоже парабола, ветви которой направлены вверх. Изобразим эти линии:

Площадь
фигуры, заключенной между двумя линиями
![]() и
и![]() ,
на отрезке
,
на отрезке![]() где
где![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]() .
.
В
нашей задаче:
![]() и
и![]() .
.
Чтобы найти пределы интегрирования a и b, нужно определить абсциссы точек пересечения этих двух линий. Находим их, решая систему уравнений:
![]()
Имеем:
![]()
Следовательно,
![]() .
.
Находим площадь фигуры:
 (кв. единиц)
(кв. единиц)
Найти площадь фигуры, ограниченной линиями:
 ,
, ,
, ,
,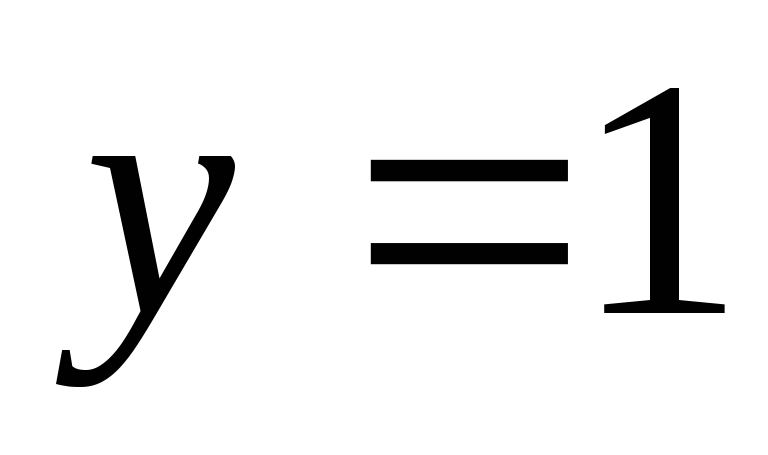 .
.
РЕШЕНИЕ:
Первая
линия представляет собой логарифмическую
кривую. Линии
![]() и
и![]() совпадают с осями
совпадают с осями![]() и
и![]() соответственно. Линия
соответственно. Линия![]() параллельна оси
параллельна оси![]() .
.
Изобразим эти линии:

Из рисунка видно, что удобнее решать эту задачу, проецируя криволинейную трапецию на ось ординат. В противном случае ее придется разбивать на две фигуры. Тогда формула для вычисления площади будет иметь вид:
![]() .
.
В
нашей задаче
![]() .
Следовательно
.
Следовательно![]() .
.
Пределы
интегрирования
![]() и
и![]() .
.
Получим:
 (кв. единицы)
(кв. единицы)
Найти площадь фигуры, ограниченной линиями:
 ,
, ,
, и расположенной в первой четверти.
и расположенной в первой четверти.
РЕШЕНИЕ:
Кривая
![]() - гипербола, кривая
- гипербола, кривая![]() - парабола с вершиной в начале координат.
- парабола с вершиной в начале координат.![]() - прямая, параллельная оси абсцисс.
- прямая, параллельная оси абсцисс.
Изобразим эти линии:

Искомая
площадь
![]() выразится как разность площадей:
выразится как разность площадей:
![]() .
.
Каждая из этих площадей может быть найдена через соответствующий определенный интеграл.
Площадь
![]() - это площадь под линией
- это площадь под линией![]() на отрезкеDF.
Найдем пределы интегрирования (абсциссы
точек D
и F,
которые совпадают
с абсциссами точек A
и B).
на отрезкеDF.
Найдем пределы интегрирования (абсциссы
точек D
и F,
которые совпадают
с абсциссами точек A
и B).
Точка А – точка пересечения прямой и гиперболы:
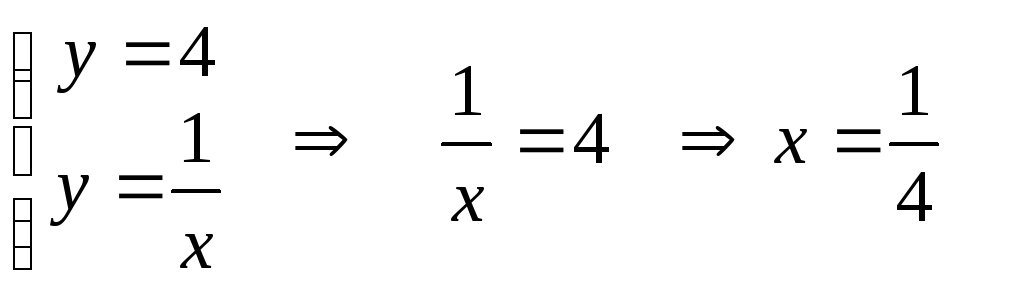
![]()
Точка В – точка пересечения прямой и параболы:
![]()
![]()
Тогда
 (кв. единиц).
(кв. единиц).
Площадь
![]() - это площадь под гиперболой
- это площадь под гиперболой![]() на отрезкеDE.
Найдем абсциссу точки E,
которая совпадает
с абсциссой точки F.
на отрезкеDE.
Найдем абсциссу точки E,
которая совпадает
с абсциссой точки F.
Точка F – точка пересечения параболы и гиперболы:

![]()
Тогда
 (кв. единиц)
(кв. единиц)
Площадь
![]() - это площадь под параболой
- это площадь под параболой![]() на отрезкеEF:
на отрезкеEF:
 (кв. единиц)
(кв. единиц)
Находим искомую площадь:
![]() (кв.
единицы)
(кв.
единицы)
Найти объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями:
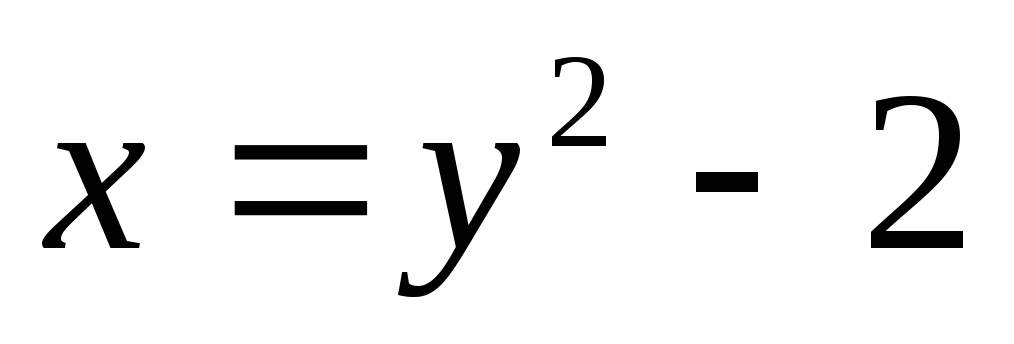 ,
, .
.
РЕШЕНИЕ:
Линия
![]() представляет собой параболу с вершиной
в точке (-2;0) и ветвями, направленными
вправо.
представляет собой параболу с вершиной
в точке (-2;0) и ветвями, направленными
вправо.![]() -
прямая, являющаяся биссектрисой первого
и третьего координатных углов.
-
прямая, являющаяся биссектрисой первого
и третьего координатных углов.
Изобразим эти линии:

Вращаемая
фигура – криволинейный треугольник
ОАВ.
Объем тела, полученного от вращения
вокруг оси
![]() криволинейной трапеции, образованной
линиями
криволинейной трапеции, образованной
линиями![]() находится по формуле:
находится по формуле:
![]() .
.
В нашем случае искомый объем выразится через разность:
![]()
Найдем эти объемы.
![]() - объем тела,
образованного вращением вокруг оси
абсцисс фигуры, ограниченной сверху
параболой
- объем тела,
образованного вращением вокруг оси
абсцисс фигуры, ограниченной сверху
параболой
![]() на отрезкеАС.
Найдем абсциссу точки С,
которая совпадает
с абсциссой точки В:
на отрезкеАС.
Найдем абсциссу точки С,
которая совпадает
с абсциссой точки В:
![]()
![]() .
.
Так
как под знаком интеграла должна стоять
функция, зависящая от х, то из исходной
функции
![]() выражаем
выражаем![]() :
:![]() .
Тогда
.
Тогда
 (куб. единиц)
(куб. единиц)
Аналогично
находим объем
![]() .
Это тело образовано вращением вокруг
оси абсцисс фигуры, ограниченной сверху
прямой
.
Это тело образовано вращением вокруг
оси абсцисс фигуры, ограниченной сверху
прямой![]() на отрезкеOD.
Тогда
на отрезкеOD.
Тогда
 (куб. единиц).
(куб. единиц).
Тогда искомый объем будет равен:
![]() (куб.
единиц).
(куб.
единиц).
5.
Вычислить объем тела, полученного от
вращения вокруг оси ординат фигуры,
ограниченной линиями:
![]() ,
,![]() .
.
РЕШЕНИЕ:
Линия
![]() представляет собой параболу с вершиной
в точке (1;-1) и ветвями, направленными
вверх.
представляет собой параболу с вершиной
в точке (1;-1) и ветвями, направленными
вверх.![]() - ось абсцисс.
- ось абсцисс.
Изобразим эти линии:

Так как вращение происходит вокруг оси ординат, то формула для вычисления объема принимает вид:
![]() .
.
Тогда
искомый объем
![]() выразится как разность:
выразится как разность:
![]() .
.
Найдем
эти объемы. Для этого найдем уравнения
кривых ОА
и ОВ
в виде
![]() :
:
![]() .
.
Решаем
это квадратное уравнение, считая
![]() параметром:
параметром:
![]()
Таким образом,
![]() -
уравнение линии АВ.
-
уравнение линии АВ.
![]() -
уравнение линии ОВ.
-
уравнение линии ОВ.
Тогда

Находим искомый объем:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
Вычислить площадь фигуры, ограниченной линиями: параболой
 ,
прямыми
,
прямыми и осью ординат.
и осью ординат.
Вычислить площадь фигуры, ограниченной линиями: ветвью гиперболы
 ,
прямыми
,
прямыми и осью абсцисс.
и осью абсцисс.
Вычислить площадь фигуры, ограниченной линиями: параболой
 ,
прямой
,
прямой и осями координат.
и осями координат.
Вычислить площадь фигуры, ограниченной линиями: параболой
 и осью абсцисс.
и осью абсцисс.
Вычислить площадь фигуры, ограниченной параболами
 ,
прямыми
,
прямыми .
.
Вычислить площадь фигуры, ограниченной линиями: параболой
 ,
прямой
,
прямой .
.
Вычислить площадь фигуры, ограниченной линиями: параболой
 ,
прямой
,
прямой .
.
Вычислить площадь фигуры, ограниченной линиями:
 ,
прямыми
,
прямыми .
.
Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями: гиперболой
 и прямыми
и прямыми .
.
Вычислить объем тела, полученного от вращения вокруг оси ординат фигуры, ограниченной кривой
 и отрезком
и отрезком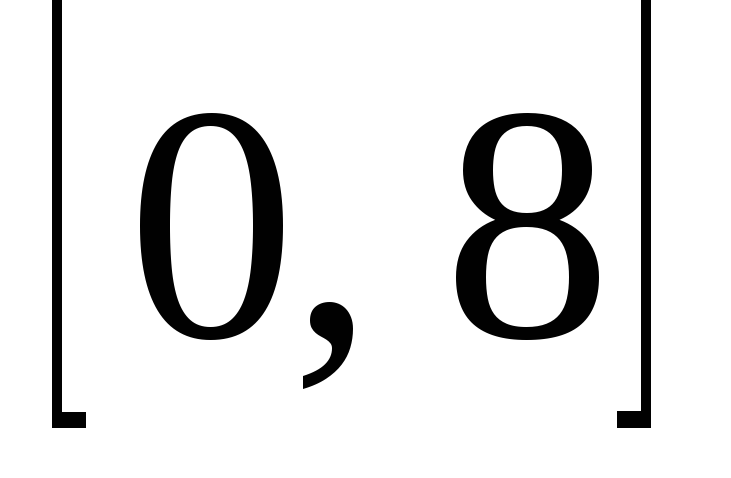 оси ординат.
оси ординат.
Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями: параболой
 и прямыми
и прямыми ,
где
,
где .
.
Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной параболами:
 .
.
Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями: кривой
 и прямыми
и прямыми .
.
Вычислить объем тела, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями: кривой
 и прямыми
и прямыми .
.
