функции многих переменных идз

ГОУ ВПО Уральский государственный педагогический университет

В.Ю. Бодряков, Н.В. Ткаленко, Н.Г. Фомина

Функции многих переменных

Индивидуальные домашние задания по дисциплине ¾Математический анализ. Часть 5. Функции нескольких переменных¿

Екатеринбург 2009

Составители: В.Ю. Бодряков, Н.В. Ткаленко, Н.Г. Фомина

2

Индивидуальные домашние задания по дисциплине "Математический анализ. Часть

5.Функции нескольких переменных". Екатеринбург, Изд-во УрГПУ, 2009, с. Индивидуальные домашние задания (ИДЗ) по дисциплине "Математический анализ.

Часть 5. Функции нескольких переменных"предназначены для студентов очной и заочной форм обучения математического факультета УрГПУ, изучающих курс математического анализа. Работа содержит 12 ИДЗ по 25 вариантов в каждом, содержащих различные задания по теме "Функции нескольких переменных". Самостоятельное решение индивидуальных заданий дает возможность углубить теоретические знания, отработать практические навыки интегрирования и освоить приложения интегрального исчисления. Во введении к работе приведены подробные примеры решения типовых заданий по теме с необходимыми методическими указаниями.

Рецензент:

c Уральский государственный педагогический университет, 2009

Введение. Методические указания к решению заданий

0.1Основные свойства функции нескольких переменных

Найти область определения D функции двух переменных: z = f(x; y) = ln(25 x2 y2) + (x2 + y2 4) и изобразить ее на плоскости (xOy): Охарактеризовать множество

D:

Решение: Область определения D: функции z = f(x; y) определяется условиями:

25 x2 y2		>	0;
x2 + y2 4		>	0;
или, эквивалентно,
x2 + y2	<	25;
x2 + y2	>	4:

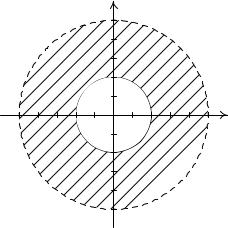
Решение данной системы уравнений может быть изображено на плоскости в виде области, заключенной между двумя концентрическими окружностями (рис. 1). Внутренняя граница принадлежит области определения D; внешняя нет.

				y
				5
				2
				1
	5		2	0	1	2	5	x
				2
				5
Рис. 1. Область D определения функции
z = f(x; y) = ln(25 x2 y2)+(x2 +y2 4)

Множество D не является ни замкнутым, ни открытым. Действительно, с одной стороны, множество предельных точек, лежащих на внешней границе, не принадлежит D: С другой стороны, множество предельных точек внутренней границы принадлежит D лишь с частью своей окрестности. Множество D ограничено, т.к. может быть целиком заключено в двумерный "шар"с центром в точке O(0; 0) конечного радиуса R = 5: Множество D связно, так любые две его точки можно соединить ломаной, целиком лежащей в D: Множество D не является компактным, так как не является замкнутым.

Ответ: Область определения D заданной функции z = f(x; y) приведена на рис. 1. Множество D ограничено, не является ни замкнутым, ни открытым, и не компактно.

0.2Вычисление пределов для функции нескольких переменных

Вычислить данный двойной предел функции нескольких переменных, а также оба повторных предела. Сравнить полученные значения между собой:

lim sin xy : x!0 sin 2xy

y!4

Решение: Считая, что предел существует, воспользуемся теоремами о пределах:

lim

sin xy

=

1

lim

sin xy

y

2x

=

1

lim

sin xy

lim y

lim

2x

=

1

1

4

1 = 2:

sin 2xy

2

sin 2xy

sin 2x

2

sin 2xy

2

x!0

x!0

x!0

y 4

x

0 sin 2x

y

!

4

y

!

4

y

!

4

!

!

Вычислим повторные пределы:

lim lim

sin xy

= lim

y

lim

sin xy

2x

= lim

y

1

1 = 2:

sin 2x

2

y

4 x

!

0 sin 2xy

y

!

4

2 x 0 sin 2xy

y

!

4

!

!

lim lim

sin xy

lim

sin 4x

= lim

sin 4x

2x

= 2

1

1 = 2:

sin 2x

x

!

0 y

4 sin 2xy

= x

!

0 sin 2x

x

0

4x

!

!

Ответ: lim

sin xy

= lim lim

sin xy

= lim lim

sin xy

= 2:

sin 2xy

sin 2xy

x!0

y 4 x

0

sin 2xy

x

!

0 y

!

4

y

!

4

!

!

0.3Исследование функции нескольких переменных на непрерывность

Исследовать функцию нескольких переменных на непрерывность:

(		1;		при	x2 + y2	= 0:
f(x; y) =	ln(1+x+y)		;	при	x2 + y2	6= 0
	x2+y2

Если функция претерпевает разрыв, исследовать тип точек разрыва. Решение: Область определения D функции f(x; y) определяется условиями:

1 + x + y > 0; x2 + y2 6= 0

и представляет открытую верхнюю полуплоскость с выколотой точкой O(0; 0) (рис. 2).

4

	y
	1
1	0	1	x
	1
Рис. 2. Область D определения функции z = f(x; y):

В любой точке (x; y) 2 D; возможно, за исключением граничных, данная функция f(x; y) непрерывна, так как является композицией элементарных непрерывных функций. Исследуем на непрерывность поведение функции f(x; y) в граничной точке O(0; 0) множества D, где непрерывность функция может быть нарушена. Для этого вычислим

	предел	ln(1 + x + y)
	lim		:
		x2 + y2
	x!0
	y!4

Для определенности положим y = kx; где угловой коэффициент k может принимать значения 1 < k < +1: В этом случае имеем:

lim

ln(1 + x + y)

= lim

ln(1 + x(1 + k))

= lim

x2 + y2

x2(1 + k)

x!0

x

!

0

x

!

0

y

!

4

1			ln(1 + x(1 + k)		= 1;
x			x(1 + k)

в зависимости от того, x

!

0+0

или x

!

0

0; соответственно. При нахождении предела

мы воспользовались тем, что

lim

ln(1+t)

= 1:

Так как в точке

O(0; 0) lim f(x; y)

=

t

!

0

t

x!0

6

y!0

f(0; 0); причем lim f(x; y)

=

1; то точка O(0; 0) является точкой разрыва второго

x!0

y!0

рода.

Ответ: Данная функция f(x; y) непрерывна в любой точке (x; y) из своей области определения D; в точке O(0; 0) функция f(x; y) претерпевает разрыв второго рода.

0.4Дифференцирование функции нескольких переменных, заданной явно

Найти первые и вторые частные производные функции z(x; y); заданной явно:

z(x; y) = ln(3xy 4):

Убедиться в том, zxy00 = zyx:00 Записать выражения для первого и второго дифференци-

алов функции z(x; y):					= f(x; y) определяется неравенством
Решение: Область определения D функцииz
y > 4=(3x): Найдем первые частные производные функции z(x; y) :
x	= (ln(3xy		x	=	3y=(3xy		4);
z0			4))0
y	= (ln(3xy		y	=	3x=(3xy		4):
z0			4))0

5

Найдем вторые частные производные функции z(x; y) :

zxx00 zyy00 zxy00 zyx00

=(3y=(3xy 4))0x

=(3x=(3xy 4))0y

=(3y=(3xy 4))0y

=(3x=(3xy 4))0x

=9y2=(3xy 4)2;

=9x2=(3xy 4)2:

=12=(3xy 4)2;

=12=(3xy 4)2:

Видим, что zxy00 = zyx:00 Выпишем выражения для первого и второго дифференциалов функции z(x; y) :

dz = z0

dx + z0

dy =

3ydx

+

3xdy

= 3

ydx + xdy

:

x

y

3xy 4 3xy 4

3xy 4

d2z = z00

d2x+2z00

dxdy+z00

d2y =

9y2d2x

24

dxdy

9x2d2y

=

9y2d2x + 24dxdy + 9x2d2y

:

(3xy 4)2

(3xy 4)2

(3xy 4)2

(3xy 4)2

xx

xy

yy

zx0

Ответ: zxx00 dz

d2z

=

3y=(3xy

y

= 3x=(3xy

4);

4); z0

=

9y2

=(3xy

4)2;

z00

=

9x2

=(3xy

4)2

;

z00

=

12=(3xy

4)2;

yy

xy

=3(ydx + xdy)=(3xy 4);

=(9y2d2x + 24dxdy + 9x2d2y)=(3xy 4)2:

0.5 Дифференцирование функции нескольких переменных, заданной неявно

Вычислить значения первых частных производных функции z(x; y); заданной неявно, в данной точке M0(x0; y0; z0) с точностью до двух знаков после запятой:

x3 + 3xyz z3 = 27; M0(3; 1; 3):

Решение: Получим выражения для первых частных производных функции

F (x; y; z) = x3 + 3xyz z3 27 = 0 :

Fx0 Fy0

откуда

=3x2 + 3yz + 3xyzx0 3z2zx0 = 0;

=3xz + 3xyzy0 3z2zy0 = 0;

zx0	=	(x2 + yz)=(z2 xy);
zy0	=	xz=(z2 xy):

Вычислим значения найденных частных производных в точке M0 :

Ответ: zx00 zy

z0

(3; 1; 3)

=

(32 + 1

3)=(32

3

1) = 2;

x

z0

(3; 1; 3)

=

3

3=(32

3

1) = 3=2 = 1; 5:

y

= (x2 + yz)=(z2 xy);

zx0 (3; 1; 3) = 2;

= xz=(z2 xy);

zy0 (3; 1; 3) = 1; 5:

6

0.6Уравнения для функции нескольких переменных и ее производных

Проверить, удовлетворяет ли указанному уравнению данная функция нескольких переменных:

@2u @2u @x2 @y2 =

Решение: Для данной функции u(x; y) производные по x и по y :

0; u = ln(x2 y2):

вычислим ее первые и затем вторые частные

@u	=	@ ln x2 y2			=	2x		;
						2 2
@x		@x			x y
@u		2	y	2
	=	@ ln x			=		2y		;
@y		@y					x2 y2

@2u	=	@		2x	= 2	x2+y2
@x2							;
		@x		x2 y2		(x2 y2)2

@2u	=	@		2y	= 2	x2+y2
@x2							:
		@y		x2 y2		(x2 y2)2

Видим, что функция u(x; y) удовлетворяет данному уравнению. Ответ: Функция u = ln(x2 y2) удовлетворяет уравнению

@2u @2u

@x2 @y2 = 0:

0.7Исследование функции нескольких переменных на локальный экстремум

Исследовать на локальный экстремум функцию нескольких переменных:

z = xy(x + y 2):

Решение: Найдем первые частные производные данной функции:

zx0	= 2xy + y2 2y;
z0	=	x2 + 2xy			2x:
y
Приравнивая их нулю, получаем систему уравнений:
y(2x + y 2)			=		0;
x(x + 2y 2)			= 0;
из которой определяем стационарные		точки		функции z(x; y) : M1(0; 0); M2(2; 0);

M3(0; 2); M4(2=3; 2=3): Для установления того, какие из этих точек являются точками локального экстремума, найдем выражения для вторых частных производных данной функции:

zxx00 zxy00 zyy00

=2y;

=2x + 2y 2;

=2x:

Значения вторых частных производных в стационарных точках функции z(x; y); а также дискриминант 4 = AC B2; соответственно, равны:

A1

= z00

(M1) = 0;

B1

= z00

(M1) =

2;

C1

= z00

(M1 = 0;

4

1 =

4;

xx

xy

yy

A2

= z00

(M2) = 0;

B2

= z00

(M2) = 2;

C2

= z00

(M2) = 4;

4

2 =

4;

xx

xy

yy

A3

= z00

(M3) = 4;

B3

= z00

(M3) = 2;

C3

= z00

(M3) = 0;

4

3 =

4;

xx

xy

yy

A4

= z00

(M4) = 4=3; B4

= z00

(M4) = 2=3;

C4

= z00

(M4) = 0;

4

4 = 4=3:

xx

xy

yy

7

Так как 41; 42; 43 < 0; то в точках M1(0; 0); M2(2; 0); M3(0; 2) экстремума нет. Поскольку 44 > 0; то в точке M4(2=3; 2=3) имеем локальный минимум функции, в котором zmin(2=3; 2=3) = 8=27:

Ответ: В точке Mmin(2=3; 2=3) функция z = xy(x+y 2) имеет локальный минимум, равный zmin(2=3; 2=3) = 8=27:

0.8Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области

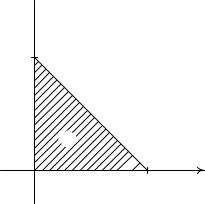
Найти наибольшее и наименьшее значения функции нескольких переменных: z = xy y2 + 3x + 4y в замкнутой области D;, ограниченной линиями x = 0; y = 0; x + y 1 = 0 (рис. 3).

Решение: Известно, что функция, определенная в замкнутой области, достигает своих наименьшего и наибольшего значений либо в стационарных точках, принадлежащих области, либо на ее границе. Поэтому необходимо выяснить, существуют ли стационарные точки функции z(x; y); принадлежащие D и исследовать функцию на экстремум.

y

1

D

0

1

x

Рис. 3. Область D; ограниченная линиями x = 0; y = 0; x + y 1 = 0:

Для первых частных производных функции z(x; y) имеем:

zx0	=	y + 3 = 0;
z0	=	x		2y + 4 = 0;
y

откуда есть стационарная точка M1( 10; 3): Так как стационарная точка M1 лежит вне области D; то ее не учитываем. Исследуем поведение функции на границе области

D:

На границе x = 0 функция z(x = 0; y) = y2 + 4y представляет собой квадратичную параболу с ветвями, обращенными вниз. Стационарная точка для этой функции определяется условием zy0 (x = 0; y) = 2y + 4 = 0; что дает M2(0; 2): Так как и стационарная точка M2 лежит вне области D; то ее также не учитываем. Следовательно, функция z(x = 0; y) = y2 + 4y достигает своих наибольшего и наименьшего значений на своих границах. А именно, в точке (0; 0) значение z(0; 0) = 0 и в точке (0; 1) значение z(0; 1) = 3:

На границе y = 0 функция z(x; y = 0) = 3x представляет собой прямую, и, следовательно, достигает наибольшего и наименьшего значений на своих границах. А именно, в точке (0; 0) значение z(0; 0) = 0 и в точке (1; 0) значение z(1; 0) = 3:

8

На границе x + y 1 = 0 функция z(x; y = 1 x) = 2x2 + 2x + 3 представляет собой квадратичную параболу с ветвями, обращенными вниз. Стационарная точка для этой

функции определяется условием zx0 (x; y = 1 x) = 4x+2 = 0; что дает M3(1=2; 1=2) 2 D: Так как zxx00 (x; y = 1 x) = 2 < 0; то в точке M3 имеем максимум z(1; 0) = 3; 5: В граничных точках (1; 0) и (0; 1) значения функции z(x; y) определены выше.

Таким образом, данная функция z(x; y); определенная в указанной замкнутой обла-

сти D; достигает своего наибольшего значения zнаибольш(1; 0) = 3; 5 в точке (1; 0) и наименьшего значения zнаименьш(0; 0) = 0 в точке (0; 0):

Ответ: zнаибольш = z(1; 0) = 3; 5; zнаименьш = z(0; 0) = 0:

0.9Изменение порядка интегрирования в кратных интегралах

Изобразить область интегрирования; изменить порядок интегрирования:

pp

1		x	2		2 x
I1 = Z0	dx Z0	f(x; y)dy + Z1		dx	Z0	f(x; y)dy:

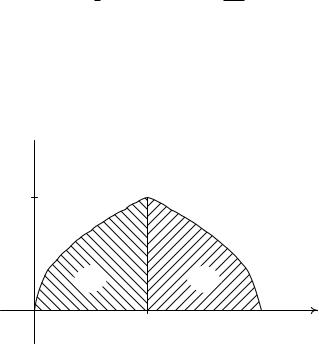
Решение: Область интегрирования D (рис. 4) данного повторного интеграла I = I1 + I2

S

представляет собой объединение двух областей: D = D1 D2: Область D1 ограничена линиями x = 1; y = 0; y = x: Область D2 ограничена линиями x = 1; y = 0; y = (2 x):

y

1

D1 D2

0

1

2

x

Рис. 4. Область интегрирования D двойного интеграла I:

Исходно при вычислении двойного интеграла I1 при фиксированной абсциссе x ордината y изменяется в пределах от 0 до кривой y = x; а уже затем x изменяется в пределах от 0 до 1: При изменении порядка интегрирования при фиксированной ординате y абсцисса x изменяется в пределах от кривой x = y2 до 1; а уже затем y изменяется в пределах от 0 до 1:

В итоге,	p
1	dx Z	x		1	1
I1 = Z		f(x; y)dy =		Z	dy Z2	f(x; y)dx:
0	0			0	y

Аналогично, при вычислении двойного интеграла I2 исходно при фиксированной абсциссе x ордината y изменяется в пределах от 0 до кривой y = (2 x); а уже затем x изменяется в пределах от 1 до 2: При изменении порядка интегрирования при фиксированной ординате y абсцисса x изменяется в пределах от x = 1 до кривой x = 2 y2; а уже затем y изменяется в пределах от 0 до 1:

9

В итоге,				p
										y2
		2			2 x				1
		I2 = Z1	dx	Z0		f(x; y)dy = Z0				dy Z1	f(x; y)dx:
1	1			1				y2
Ответ: I = R0	dyyR2	f(x; y)dx + R0				dy		R1	f(x; y)dx:

0.10Вычисление двойных интегралов

Вычислить двойные интегралы в указанных областях:

0.10.1
I1 = ZZ (xy 9x5y5)dxdy;					D1 : x = 1; y = p3				; y = x2;
							x
	D1
0.10.2	=	ZZ y2 cos 2 dxdy;			D2 : x = 0; y = p2 ; y = 2x:
I2
			xy
		D2

У к а з а н и е. Проверить правильность ответа можно повторным расчетом с иным порядком интегрирования.

Решение: p

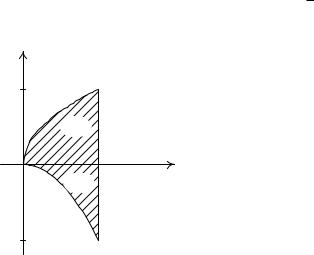
10.1. Вычислим двойной интеграл I1 в области D1 (рис. 5). Кривые y = 3 x и y = x2 пересекаются в точках (0; 0) и ( 1; 1):

	y
	1
		D11
	0	D	1	x
		12
	1
Рис.	5.	Область		интегрирова-
ния D1		двойного интеграла I1:

Область интегрирования D1 данного повторного интеграла I1 удобно представить в виде объединения двух непересекающихся (за исключением точки (0; 0)) областей: D1 =

10