Теоремы о пределах. Глава 3. Раздел 1

ГФ Первый курс Осень 2009 Высшая математика Лисеев И.А.

	Т е о р е м а . Если функция имеет конечный предел А
		l i m f ( x ) A ,	R ,	A R ,
		x
	то существует такая окрестность , в которой f ( x ) ограничена.
рис....для конечного		рис.... для бесконечного

2 . Об яз а т е л ьн о л и о г р а н и ч е н н а я в е л и ч и н а и м е е т п р е де л ?

Ограниченная величина может не иметь предела. Поясним на примере , что

здесь имеется в виду. (Это будет, так сказать, "контр пример" для теоремы из предыдущего пункта)

П р и м е р . | s i n x | 1 для всех х . Это означает, что f ( x ) = s i n x - ограничена на всей области определения. Но ...

l i m sin x не существует

x

При доказательстве того, что такого предела не существует, сначала покажем, что у sin x при x нет конечного предела, а затем покажем, что нет бесконечного предела.

1) Если l i m sin x c и с R ,		то для >		0 (возьмѐм = ¼ ) долж-
x
но найтись х 1 такое,	что при всех х > x 1		было бы: | sin x – c | < ¼ . При этом
- полоса точки с	будет иметь ширину ½ .		(Рисунок.)	Но … Но график

f ( x ) = si n x никогда не окажется внутри такой полосы, так как колебание sin x составляет 2 единицы. Значит, никакое число с R не является пределом l i m sin x .

			x
2) Если l i m sin x ,		то для М (возьмѐм М = 2 )	должно найтись х 1 та-
x
кое, что при всех х > x 1	было бы: | sinx | > 2 . Но такого не может быть. Нико-
гда не будет | sinx | > 2 . Значит, не является пределом			l i m sin x .
			x
В следующих двух пунктах выясним, в чѐм состоит различие между понятиями "бесконечно большая вели-
чина" и "неограниченная величина"?	Кто находится на уровне оценки "хорошо" или "отлично", разберитесь в этом.
3 . Н е о г р а н и ч е н н о с т ь б е с к о н е ч н о б о л ь ш о й в е л и ч и н ы .
Т е о р е м а . Если		l i m f ( x ) , г д е – конечное или бесконечное,
		x

то существует окрестность , в которой функция f ( x ) неограничена.

Рисунок...

Доказательство. Возьмѐм произвольное М . Существует окрестность, где | f ( x ) | > M . То есть, при х 1 , принадлежащем этой окрестности, будет | f ( х 1 ) | M . Значит f ( x ) неограничена в этой окрестности . #

21

Высшая математика (Ли…) Раздел 1. Функции, пределы, непрерывность. Гл. 3. Теоремы о пределах.

4 . Об я з а т е л ь н о л и н е о г р а н и ч е н н а я в е л и ч и н а я в л я е т с я б е с к о н е ч н о б о л ь ш о й ?

Неограниченная величина не обязательно является бесконечно большой. Поясним на примере, что здесь

имеется в виду.
П р и м е р .	Функция z		= t s i n t – неограниченная в любой окрестности	. Но у неѐ
вообще нет предела при t		.	Нет М -полосы , в которой бы находился график после некоторо-
го t 1 (при t > t 1 ).	И ничего не меняется, если взять не просто бесконечность, а бесконечность с каким-
то знаком.

Рисунок.

§ 8 . ПРОИЗВЕДЕНИЕ БЕСКОНЕ ЧНО МАЛОЙ НА ОГРАНИЧ ЕННУЮ

Сформулируем теорему для функций.

Т е о р е м а .

Пусть

l i m ( x )

0 (где - конечное или беско-

x

нечное) .

Пусть в некоторой проколотой окрестности функ-

ция h ( x )

ограничена.

Тогда

l i m (x) h(x) 0 .

x

Здесь

( x ) – бесконечно малая при х

, а h ( x ) ограничена в некото-

рой проколотой окрестности

. Утверждается, что произведение

(x) h(x)

будет бесконечно малым при х

.

Кратко говорят так:

произведение бесконечно малой величины на ограниченную

есть величина бесконечно малая.

Д о к - в о 3 .

б.м. огр. = б.м.

Д о к а з а т е л ь с т в о .
Обозначим окрестность , в которой h ( x )					ограничена через U1 ( ) .
В силу ограниченности		h ( x ) в этой окрестности,			существует такое число M,			что в
этой окрестности будет выполняться неравенство
		| h ( x ) | M .				(1)
Далее …	Возьмѐм > 0 . Рассмотрим 1					= / M .
Так как ( x ) 0 при х ,				то существует проколотая окрестность				,
обозначим еѐ U	( ) ,	в которой с	1	будет выполняться неравенство
	2
		| ( x ) | <	1 = / M .			(2)
Теперь рассмотрим пересечение				окрестностей		U1 ( ) и	U 2 ( ).	Это
тоже будет окрестность (проколотая окрестность)					(сделать рисунки);		обозначим еѐ без
индекса U ( ) . В этой окрестности будут выполняться оба неравенства (1) и								(2).
				22

ГФ Первый курс Осень 2009	Высшая математика							Лисеев И.А.
Имеем в окрестности U ( ) :
	| (x) h(x)| = | (x)| |h(x)| < /M M = .
Таким образом, для взятого > 0		нашлась окрестность U ( )						такая, что во
всех точках этой окрестности выполняется неравенство | (x) h(x)| <								. Это озна-
чает, что ( x ) h ( x )	0 при х .	#
П р и м е р ....		l i m	sinx	l i m	(	1	sinx ) 0.
	x		x	x		x

§9 . П Е Р Е Х О Д К П Р Е Д Е Л У В Н Е Р А В Е Н С Т В А Х

1. Т е о р е м а дл я по с л е до в а те л ь н ос те й .

Те о р е м а . Если элементы сходящихся последовательностей { x n } и { у n } , начи-

ная с некоторого номера, удовлетворяют неравенству

x n у n ,

то и их пределы l i m x n

и

l i m у n

удовлетворяют такому же неравенству

l i m x n

l i m у n .

Д о к а з а т е л ь с т в о . Для начала немножко конкретизируем условие теоремы. Во-

первых,

обозначим

l i m x n = A

и

l i m у n = В . Значит,

теорема утверждает, что А ≥ В.

B

y n

Во-вторых,

пусть неравенство x n у n

выполняется,

А

x n

начиная с номера

n 1 .

Доказательство поведѐм от противного.

Пусть А < В . Возьмѐм = ( В – А ) / 3 . Начиная с n 2 ,

y n U ( B , ) , а на-

чиная с n 3

, х n U ( А , ) ,

то есть после n 2 и n 3 будет:

x n < у n .

После n = ma x ( n 1 , n 2 , n 3 ) должны выполняться оба неравенства:

x n у n

и

x n < у n ,

что невозможно.

Значит, А В .

#

Краткая запись теоремы:

x n у n

l i m x n

l i m у n .

Понятно, что :

если в условии теоремы принять

x n ≤ у n

то будет

l i m x n

≤ l i m у n .

Это просто другая запись с изменѐнными обозначениями того же самого, что утверждает теорема.

23

Высшая математика (Ли…)	Раздел 1. Функции, пределы, непрерывность. Гл. 3. Теоремы о пределах.
2 . Т е о р е м а дл я ф у н к ц и й .

Т е о р е м а . Если в какой-то проколотой окрестности конечной точки или в какой-

то окрестности бесконечной точки выполняется неравенство
			( х ) p ( x )
и существуют конечные пределы			l i m ( x ) A и	l i m p(x) B ,
			x	x
то		l i m ( x ) l i m p( x )
		x	x
	рис.... = +
	С л е д с т в и е . Если в некоторой проколотой окрестности точки
	(х) А и существует	l i m	( х ) при х , то	l i m ( x )	A .
				x

Сформулируем такое следствие для последовательностей.

Если х n ≤ c , начиная с некоторого n , и последовательность х n сходится, то li m х n ≤ с .

	Краткая запись :		x n ≤ с	l i m x n ≤ с .
	А если х n	≥ c , …….	(закончите сами)
З а м е ч а н и е .		Пределы А	и В могут быть бесконечными определѐнного знака.

В частности, если мéньшая величина стремится к + , то и бóльшая величина стремится к + .

!З а м е ч а н и е . Если в условии теоремы требовать выполнения строгого неравенства

f ( х ) > p ( x ) , то в заключении всѐ равно можно утверждать только, что имеет место нестрогое неравенство :

f ( х ) > p ( x )

l i m (x)

l i m p (x) .

x

x

Из

a n

> b n

н е l i m a n

> l im b n .

Можно утверждать только, что

l i m a n l i m b n .

Подтвердим это примером.9

П р и м е р .

( когда ( х )

> g ( x ) ,

но всѐ равно

l i m ( х ) = l i m g ( x ) ).

1 / x

и 1 / x 2

при

х > 1 .

Или привести пример для последовательностей ?

При

x > 1

1

>

1

, а

lim

1

= lim

1

.

Рисунок.

2

→+

→+ 2

§ 1 0 . Т Е О Р Е М А О " З А Ж А Т О Й " П Е Р Е М Е Н Н О Й

Эту теорему называют ещѐ теоремой о двух милиционерах … Если идут два милиционера ... Причѐм оба идут в один и тот же пункт милиции. А между этими милиционерами идѐт гражданин. Спрашивается, куда придѐт этот гражданин?

9 Для доказательства того, что какое-то утверждение не выполняется, достаточно привести один пример того, что это утверждение не выполняется.

24

ГФ Первый курс Осень 2009	Высшая математика		Лисеев И.А.
Рассмотреть только теорему для последовательностей. ?
1 . Т е о р е м а дл я по с л е до в а те л ь н ос те й .
Т е о р е м а . Пусть даны три последовательности		{ x n } ,{ у n } и { z n } ,	причѐм, начи-
ная с некоторого n выполняется неравенство
	x n у n z n .
Пусть последовательности { x n } и { z n } имеют один и тот же конечный (из R +)
или бесконечный определѐнного знака предел .		Тогда последовательность { у n }
также имеет предел равный .

Доказательство проведѐм для случая, когда предел к о н е ч е н ( = А ).

Д о к а з а т е л ь с т в о . Пусть неравенство из условия теоремы выполняется при

n > n 1 :	x n у n z n .									Д о к - в о 4 .
	Обозначим предел последовательностей				{ x n } и { z n } через А. Возьмѐм
> 0 .
При n > n 2 :		| x n - А | <	или	А -		x n		А +	.
При n > n 3 :		| z n - А | <	или	А -		z n		А +	.
При n > ma x ( n 1		, n 2 , n 3 ) имеют место все три написанные двойные неравенст-
ва. Нам нужны обведѐнные их части.
		А - x n	у n z n А +					,
то есть,
	А - у n А +			или	| у n		-	А | < ,
а это означает, что		у n А .		#
2 . Т е о р е м а дл я ф у н к ц и й .
Т е о р е м а . Пусть функции f ( x ) , p ( x )				и h ( x ) определены в некоторой проколотой
окрестности конечной или бесконечной точки .					Пусть в этой окрестности
		f ( x ) p ( x ) h ( x ) .
Пусть существуют равные (конечные или бесконечные опр еде лѐн н ог о з н а -
ка ) пределы
		l i m f ( x )		и	l i m h( x ) .
		x			x
Обозначим их		. Тогда существует l i m			p ( x ) при х и он равен .
			l i m p( x ) .
			x

ри с .. .. = с , + .

При м ер . (где используется эта теорема)

25

Высшая математика (Ли…)

Раздел 1. Функции, пределы, непрерывность. Гл. 3. Теоремы о пределах.

З а д а н и е . Разберите по учебнику доказательство первого замечательного предела.

§ 1 1 . Т Е О Р Е М А О Б О Д Н О С Т О Р О Н Н И Х П Р Е Д Е Л А Х

Окрестности

U( c ) ,

U ° ( c ) ,

U( )

мы считаем (называем) двусторонними

окрестностями.10

Окрестности

U( c + ) ,

U( c – ) , U ( + ) ,

U ( - )

мы считаем (называем) одно-

сторонними окрестностями.

,

= с R

= , мы называем о б ы ч -

Предел l i m

f ( x )

если

или

x

н ым

пределом (просто пределом) или пределом "б е з о г р ан и ч е н и й ", или пределом

по двусторонней окрестности,

чтобы отличить его от о д н о с то р о н н и х

пределов,

когда

= с + или

с – ,

или

когда = + ,

или

= – .

Здесь мы рассмотрим связь предела функции по двусторонней окрестности с од-

носторонними пределами.

Односторонние пределы существуют и равны тогда и только то-

гда, когда существует простой (двусторонний) предел функции в рас-

сматриваемой точке. При этом двусторонний предел равен односто-

ронним пределам.

Дадим более точную формулировку … Но сначала поясним обозначения …

( = с R

или

= ; в теореме будут фигурировать – = с –

и + =

с + , в случае бесконечности это будут						= +	и	= –	)
( может быть любым:			с ,	с +	или	с – , , +		или	= –	)
Т е о р е м а .		(Необходимое и достаточное условие существования предела)
Пусть ,		– конечные или бесконечные. Пусть функция f ( x )								определена в
некоторой двусторонней проколотой окрестности .
Тогда:
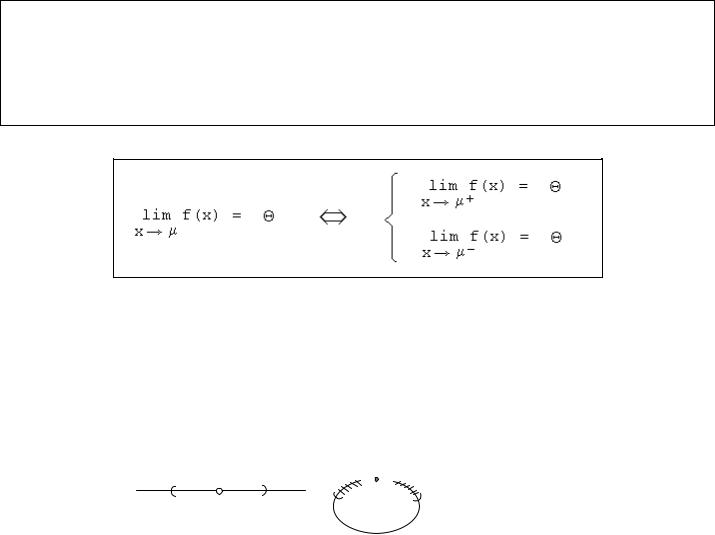
	1) Если существует предел по двухсторонней окрестности, то есть обыч-
ный предел без ограничений:				l i m	f ( x ) ,		то существуют и односторонние пре-
				x
делы l i m	f ( x ) и l i m		f ( x ) ,		и эти пределы равны .
x		x

10 Допускаются оба варианта написания: двусторонний и двухсторонний (смотрите орфографический словарь).

26

ГФ Первый курс Осень 2009 Высшая математика Лисеев И.А.

2) Если существуют односторонние пределы l i m f ( x )		и l i m f ( x ) ,
	x	x
оба равные ,	то существует и обычный предел без ограничений	по двусторонней
окрестности	l i m f ( x ) и он равен .
x

Краткая запись теоремы:

Д о к а з а т е л ь с т в о . 1) Пусть l i m f (x) . Возьмѐм произвольную окрестность

x

U ( ) . Для неѐ обязательно найдѐтся (двусторонняя проколотая) окрестность U ( )

такая, что: х U ( ) f( x ) U ( ) .

Окрестность U ( ) можно представить как объединение односторонних окре-

стностей U ( ) = U ( – ) U ( + ) .

=

При этом U ( + ) U ( ) и U ( – ) U ( ) .

Если условие f ( x ) U ( ) верно для всей окрестности, то оно верно и для еѐ частей (для односторонних окрестностей точки ). То есть нашлись такие односто-

ронние окрестности точки ,		для которых …
для одной :	x U ( + ) U ( ) f ( x ) U ( )				l i m	f (x) ;
					x
для другой :	x U ( – ) U ( )		f ( x ) U ( )		l i m	f (x) .
					x
2) Пусть l i m f (x)		и	l i m f ( x ) .
	x		x
Возьмѐм окрестность .			Существуют такие окрестности – и + , для

всех х из которых f ( x ) U( θ , ) . Вместе эти окрестности составляют полную проколотую окрестность точки . Значит, нашлась проколотая полная окрестность точ-

ки такая, что для всех	х из этой окрестности	f ( x ) U( θ , ) .	Это значит,
что l i m f (x) .	#
x
	27

П р и м е р .

Высшая математика (Ли…)	Раздел 1. Функции, пределы, непрерывность. Гл. 3. Теоремы о пределах.
С л е д с т в и е .	Если односторонние пределы хотя и существуют, но различны,

простой предел (по двусторонней окрестности) не существует.

# Это утверждение следует как из данной теоремы, так и из второго определения предела функции, в котором требуется, чтобы при любом стремлении аргумента к своему предельному значению функция имела один и тот же предел. А в условии следствия при подходе аргумента к своему предельному значению справа получается один предел функции, а при подходе аргумента к своему предельному значению слева получается другой предел функции. #

В этом примере оба односторонних предела существуют, но не равны между собой. В этом случае простого предела (по двусторонней окрестности) не существует. Рисунок.

| |

lim 0+

= 1 ,	lim 0−	|	|		= −1		lim 0	|	|	− не существует.

§ 1 2 . З А М Е Н А П Е Р Е М Е Н Н О Й П Р И В Ы Ч И С Л Е Н И И П Р Е Д Е Л А

( П Р Е Д Е Л С Л О Ж Н О Й Ф У Н К Ц И И )

Напомним, сложная функция – это функция, аргумент у которой сам является функцией.

1 . Т ео р ема .

Начнѐм с краткой записи.

Пусть

	y y(t) ,		t t(x)
l i m y ( t(x) ) ?	l i m	t(x)
	x
x
	l i m	y ( t)

t

и функция y(t(x)) определенав некот окр - ти точки x .

		l i m y (t(x))
		x

Т е о р е м а .

1) Пусть – конечно или бесконечно и пусть существуют конечные или бесконечные пределы

l i m t( x )	и	l i m y( t ) .
x		t

2) Пусть в некоторой проколотой окрестности точки определена сложная функция у ( t ( x ) ) ,

Тогда: существует (конечный или бесконечный) предел этой слож-

ной функции l i m y( t( x )) и этот предел равен .)

x

Д о к а з а т е л ь с т в о .....

28

ГФ Первый курс Осень 2009															Высшая математика														Лисеев И.А.
	Эту теорему мы всѐ время применяем при вычислении пределов функций, аргу-
менты которых сами являются функциями.																		В частности, такие пределы приходится
вычислять при построении (без исследования функции с помощью производной) графиков
сложных функций.
	2 . Пр им ер ы .
	П р и м е р ы .					1.	lim				sin				= ?		= sin				,		=	.
									0			2												2
		lim				=	0 ,		lim				sin			=	0	11				lim		0	sin		=	0 .
			0 2								0															2
					1																	1
	2. l i m 2 x					... ... ;											3.		l i m 2 x ... ...							0 ;
		x 0																	x 0
	4.		l i m		(sin		1) 2			l i m				t 2		0 ,		где обозначено						sin(1/x) = t .
		x					x			t 0
	П р и м е р ы использования данной теоремы при построении графиков функций:
=	21/			и			= 1 .
			1
	y( x)		2x															y( x)		atan 1
																						x
							8																	3
							7
							6																	2
							5																	1
							4
y( x)							3										y( x)
							2													10	8	6	4	2	0	2	4	6	8	10
							1																	1
																										– /2
		10		8	6	4	21	0	2	4		6		8	10									2
							2																	3
								x																	x
	Рассмотрим ещѐ пример,									когда условия теоремы не выполняются :
															lim		1			= ?
																		1
															→0
																∙ sin
			=		1	1 .			=	1		,			= ∙ sin 1			.		lim→0			1	1	=	?	х = 0 .
				∙sin																			∙sin
	Здесь в любой сколь угодно малой окрестности точки																					= 0 величина sin 1							принимает зна-
чение 0		, и, следовательно, функция, стоящая под знаком предела неопределенна.																											То есть усло-
вие	2)	теоремы не выполняется.										При этом по теореме предел получается равным ,																		а на самом
	11 Будем считать, что это (lim 0 sin = 0 ) мы непосредственно доказали с помощью определения предела .
																		29

Высшая математика (Ли…)

Раздел 1. Функции, пределы, непрерывность.

Гл. 3. Теоремы о пределах.

1 104

=

1

деле предела не существует.

На рисунках изображѐн график функции

, построен-

1

8000

∙sin

ный в МатКаде.

6000

y(x)

4000

2000

0.008	0.006	0.004	0.002	0	0.002	0.004	0.006	0.008
				x

100

80

60

y(x)

40

20

1		0.8	0.6	0.4		0.2	0	0.2	0.4	0.6	0.8	1
							x

З а м е ч а н и е . Приведѐнная теорема позволяет считать пределы сложных функций с помощью замены переменной. При этом не требуется непрерывности внутренней в внешней функций. Это позволяет вывести таблицу эквивалентностей, не дожидаясь введения понятия непрерывности функций.

--- При "естественных" договорѐнностях об операциях с бесконечностями и о делении на ноль (смотрите § о пределах результатов арифметических операций) получается, что правило о подведении знака предела под знак функции применимо не только к непрерывным функциям.

3 . Вы чи сле ние пр е дела по ка з ат ельно ст епенно й ф у нк ци и .

……..a(x) > 0 .

Используем основное логарифмическое тождество и теорему о пределе сложной функции .

…….

	lim			= (lim				lim
								)
	Это равенство имеет место. В т.				х =		у функций а ( х ) и р ( х ) нет разрыва первого рода.

30