1.2. Интегрирование дифференциального уравнения изогнутой оси балки

Чтобы получить аналитические выражения прогибов и углов поворота сечений, необходимо найти решение дифференциального уравнения (1.5).

Интегрируя его первый раз, получим

. (1.6)

Это выражение определяет закон изменения углов поворота сечений (касательной) по длине балки. Уравнение изогнутой оси получим после повторного интегрирования

. (1.7)

Для вычисления интегралов в выражениях (1.6) и (1.7), необходимо сначала написать аналитические выражения изгибающего момента и жёсткости. Постоянные интегрирования СиDнаходятся из граничных условий, которые зависят от способа закрепления балки.

Для уяснения сказанного рассмотрим примеры:

1. Определим прогибы и углы поворота сечений балки, показанной на рис.1.1. Считаем жёсткость балки постоянной: EJ = const. Запишем уравнение изгибающего момента

M = – M_A + R_A ∙ x = – Pℓ + Px. (a)

Дифференциальное уравнение

. (б)

Интегрируя один раз, получим

. (в)

Интегрируя ещё раз, имеем

. (г)

Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных имеем следующие граничные условия:

• при х = 0;

• при х = 0υ = 0.

Из уравнений (в) и (г) получим C = D = 0.

Очевидно, что наибольший прогиб имеет место под силой (см.рис.1.1). Подставив х = ℓв уравнение (г), найдём

.

Знак «­–» говорит о том, что перемещение происходит вниз (в отрицательном направлении оси υ).

2. Определим прогибы и углы поворота сечений двухопорной балки постоянного сечения, нагруженной равномерно распределённой нагрузкой (рис.1.3).

Рис.1.3

.

.

Так как EJ = const, ;

. (д)

. (е)

На опорах прогиб равен нулю, граничные условия:

• при х = 0υ = 0;

• при х = ℓυ = 0.

Из первого условия следует, что D = 0, из второго условия: .Следовательно,.

Найденные значения СиDподставим в уравнения (д) и (е) и получим готовые к употреблению уравнения углов поворота сечений и прогибов:

,

.

Из рис.1.3 видно, что наибольший по величине угол поворота сечения имеет место на опоре при х = 0:

;

а наибольший прогиб в середине пролёта при х = ℓ/2:

,

.

Из рассмотренных примеров очевидно, что постоянные интегрирования С и D имеют физический смысл: С – угол поворота сечения в начале координат (уравнения (в) и (д)); D – прогиб в начале координат (уравнения (г) и (е))

С = EJθ₀ , D = EJυ₀ .(1.8)

В наших примерах балки имели по одному участку. В случае произвольной нагрузки необходимо составить несколько дифференциальных уравнений, каждое из которых отвечает своему участку. Число постоянных равно удвоенному числу участков. Граничные условия приведут к системе уравнений, число которых равно числу постоянных интегрирования. Однако необходимость решения системы уравнений сильно усложняет задачу. Для балок постоянной жёсткости (EJ = const) была предложена такая форма представления решения дифференциального уравнения, которая обеспечивает равенство постоянных интегрирования на границах участков. При любом числе участков – две постоянных (1.8).

1.3. Уравнение изогнутой оси по методу начальных параметров

1. Балка с одним участком

В уравнениях изогнутой оси (г) и (е), полученных в примерах предыдущего параграфа, каждая из нагрузок – сосредоточенная Р и распределённая q – умножаются на свой множитель х³/6 (х³/3!) и х⁴/24 (х⁴/4!) соответственно. Ясно, что сосредоточенный момент М после двойного интегрирования должен умножаться на х²/2 (х²/2!). Удобно записывать функции υ и θ в стандартном виде – по методу начальных параметров, выражая их через перемещения и нагрузки в начале координат.

Для балки с равномерно распределённой нагрузкой q = q₀и сосредоточенными усилиямиМ₀иQ₀(рис.1.4) уравнение изогнутой оси имеет вид:

. (1.9)

Уравнение углов поворота сечения получается дифференцированием (1.9):

. (1.10)

Рис.1.4

Направления нагрузок М₀, Q₀иq₀приняты такими, чтобы изгибающий момент в произвольном сечении на расстояниихот начала координат получился положительным. Поэтому в формулах (1.9) и (1.10) стоят знаки «+». Начальные параметрыEJυ₀иEJθ₀могут быть найдены из граничных условий:

• при х = ℓ υ = 0;

• при х = ℓ θ = 0.

Ещё раз подчёркиваем, что в такой форме уравнения могут быть записаны для балок постоянной жёсткости (EJ = const).

2. Балка с несколькими участками (с произвольной нагрузкой)

Рассмотрим сначала балки с двумя участками: на расстоянии х = с от начала координат приложен сосредоточенный момент М (рис.1.5, а), сосредоточенная сила Р (рис.1.5,б), начинается распределённая нагрузка q (рис.1.5,в). В точке х = с имеет место скачок в одной из производных функции υ (см. п.1.1):

;;.

а б в

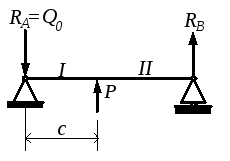
Рис.1.5

Очевидно, что при наличии скачка в любой производной ординаты упругой линии получают две ветви с различными аналитическими выражениями в связи с тем, что уравнения изгибающего момента для каждого участка различны. Для балок на рис.1.5 покажем изогнутую ось (рис.1.6).

Рис.1.6

Уравнение для первого участка может быть записано по формуле (1.9)

. (а)

По этому уравнению построим упругую линию. На первом участке она изображена жирной линией, на втором – пунктирной. Пунктирная линия не совпадает с истинной кривой изогнутой оси на втором участке, которая проведена жирной линией. Не останавливаясь на доказательстве, запишем условие сопряжения ветвей упругой линии:

. (1.11)

где N_n– скачок вn–й производной.

В соответствии с формулой (1.11) уравнения изогнутой оси для балок на рис.8.5 будут следующими:

; (а)

; (б)

. (в)

Слагаемые, расположенные левее знака |_I,IIотносятся к первому и ко второму участкам балки; а слагаемое, расположенное левее знака|_II, относится только ко второму участку. Ясно, что если участков много, то для каждого последующего записывается свой «довесок» с соответствующим множителем(х – с_i ).Начальные параметры – перемещенияEJυ₀иEJθ₀– находятся из граничных условий. Для балок на рис.8.5 они следующие:

• при х = 0υ = 0;

• при х = ℓυ = 0.

Из первого условия следует, что EJυ₀ = 0. Из второго условия можно найти EJθ₀ (на шарнирной опоре угол поворота нулю не равен – см.рис.1.6).

Итак, уравнение изогнутой оси по методу начальных параметров имеет следующий вид

(1.12)

где М₀, Q₀иq₀– усилия в начале координат;

М_i, Q_iиq_i– усилия в произвольном месте балки;

c_i– координата приложения сосредоточенных усилий или координата начала распределённой нагрузки.

Уравнение углов поворота сечений получается дифференцированным (1.12):

. (1.13)

При выводе уравнений (1.12) и (1.13) считали, что распределённая нагрузка действует от точки х = с до конца балки. Если такая нагрузка действует на участке отх = с₁до х = с₂, то её можно рассматривать как результат наложения двух нагрузок, показанных на рис.1.7. В уравнения обязательно добавляются слагаемые, учитывающие действие компенсирующей нагрузки.

Рис.1.7

Рассмотрим пример. На рис.1.8 изображена балка с произвольной нагрузкой, имеющая четыре участка. Запишем для неё уравнение изогнутой оси, приняв начало координат на левом конце

Рис.1.8

Начальные параметры здесь не равны нулю и могут быть найдены из граничных условий:

• при х = 2υ = 0;

• при х = 8υ = 0.

Придётся решить систему уравнений

Разграничительные линии показывают, какие слагаемые формулы необходимо учитывать при записи граничных условий или при подсчёте перемещения в какой-либо точке балки. Учитываются только те слагаемые, у которых множитель (x – c_i )> 0.