2.2. Расчёт методом сил

В этом методе в качестве неизвестных принимаются реакции опор или внутренние усилия. Порядок расчёта рассмотрим на примере простой балки, степень статической неопределимости которой равна единице (рис.2.2,а).

1. Отбрасываем «лишнюю» связь, превращая тем самым заданную балку в статически определимую. Полученная балка называется основной системой. В качестве «лишней неизвестной может быть взята любая, не равная нулю реакция (реакция опоры R_Bили момент в заделкеМ_А), или изгибающий момент в любом поперечном сечении. Для рассматриваемой балки самое простое – убрать правую опору. Тогда «лишняя» неизвестная – реакция этой опорыR_B = X₁.

2. Загружаем основную систему заданной внешней нагрузкой и «лишней» неизвестной. Получим так называемую эквивалентную систему (рис.2.2,б).

3. Составляем условие совместности деформаций. Оно состоит в отрицании вертикального перемещения точки В:

, (2.1)

где ∆₁– перемещение точки приложения силы Х₁по направлению её действия;

–перемещение точки приложения силы Х₁, вызванное действием этой силы (рис.2.2,г);

∆_1Р– перемещение точки приложения силы Х₁, вызванное действием внешней нагрузки (рис.2.2,в).

Перемещение от неизвестной Х₁удобно представить в виде

,

где δ₁₁– перемещение, вызванное действием единичной силыХ₁ = 1.

Таким образом, уравнение (2.1) принимает вид

δ₁₁Х₁ + ∆_1Р = 0. (2.2)

Здесь уравнение совместности деформаций записано в стандартной (канонической) форме. Оно имеет такую форму вне зависимости от того, какая принята «лишняя» неизвестная – сила или момент.

Для определения коэффициентов уравнения (2.2)можно воспользоваться любым из изложенных в главе 1 методов: методом начальных параметров или методом Мора. Обычно используют метод Мора, так как он особенно эффективен при расчёте многократно статически неопределимых балок. Найдём коэффициенты уравнения (2.2), воспользовавшись формулой Мора и вычисляя интегралы по правилу Верещагина (рис.2.3):

а
б
в
г

Рис.2.2

,

где ω₁– площадь эпюры;

m₁– ордината под центром тяжести указанной площади, измеренная на той же эпюре. Мы «перемножили» эпюру саму на себя.

Рис.2.3

.

После подстановки значений δ₁₁и ∆_1рв (2.2) получим

.

Далее строим эпюры Q и М так же, как мы это делали при расчёте статически определимых балок (рис.2.4). Задача решена, статическая неопределённость раскрыта.

Рис.2.4

2.3. Многопролётные неразрезные балки

В машиностроении и в строительстве часто применяют статически неопределимые балки, имеющие несколько промежуточных опор, – их называют неразрезными. Существенное значение при расчёте таких балок имеет рациональный выбор основной системы.

На рис.2.5,а показана трижды статически неопределимая неразрезная балка. По первому варианту основной системы (рис.2.5,б) за неизвестные приняты опорные реакции Х₁, Х₂, Х₃. По второму варианту основной системы (рис.2.5,д) неразрезная балка превращается в четыре простых двухопорных балки постановкой шарниров над промежуточными опорами; и лишними неизвестными являются изгибающие моменты в сечениях балки над промежуточными опорами, также обозначенные Х₁, Х₂ и Х₃.

Для обоих вариантов система канонических уравнений метода сил имеет одинаковый вид

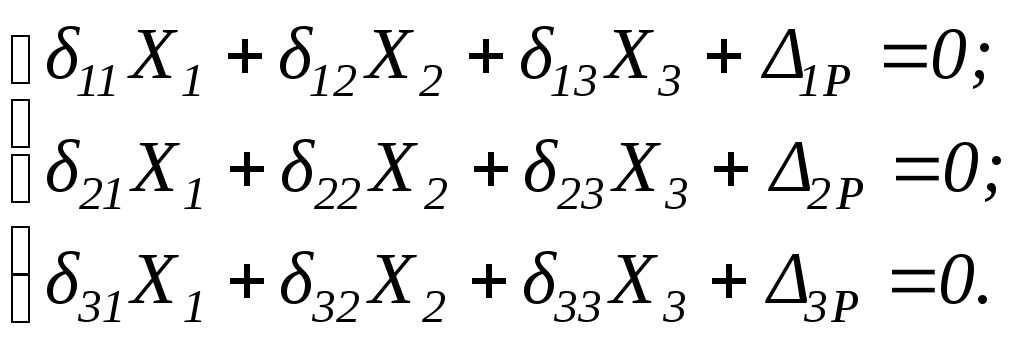(2.3)

В первом варианте основной системы смысл канонических уравнений состоит в отрицании вертикальных перемещений опорных точек 1,2,3оси балки. Во втором варианте смысл канонических уравнений состоит в отрицании углов раскрытия двух бесконечно близких сечений над промежуточными опорами. По первому варианту эпюра моментов от заданной нагрузки распространяется на всю балку (рис.2.5,в) и эпюра моментов от единичного усилия также распространяется на всю балку (рис.2.5,г). Каждое из уравнений системы содержит все неизвестные.По второму варианту эпюра моментов от нагрузки в каждом пролёте распространяется только на свой пролёт (рис.2.5,е),а эпюра моментов от единичных усилий – только на два соседних пролёта (рис.2.5,ж,з,и). Поэтому у насδ13 = δ31 = 0. При любом количестве неизвестных в каждом уравнении системы будет не более	а	Рис.2.5
	б
	в
	г
	д
	е
	ж
	з
	и

трёх ненулевых неизвестных Х_i. Поэтому второй вариант основной системы значительно проще, особенно – при большом числе неизвестных.

Итак, для один раз статически неопределимых балок в качестве лишней неизвестной лучше всего принимать реакцию одной из крайних опор. Для дважды и более статически неопределимых балок в качестве лишних неизвестных лучше принимать моменты на промежуточных опорах.

а
б
в
г
д

Рис.2.6

Рассмотрим пример расчёта дважды статически неопределимой балки (рис.2.6,а). Эквивалентная система на рис.2.6,б; лишние неизвестные – моменты на опорах. Система уравнений метода сил

(2.4)

Коэффициенты уравнений (2.4) находим методом Мора – Верещагина. Поскольку жёсткость балки постоянная и справа в уравнении стоит ноль, на EJможно сократить.

- эпюрунадо «умножить» саму на себя.

Для этого нарисуем эту эпюру дважды (рис.2.7):

.

Рис.2.7

- эпюрунадо «умножить» на(рис.2.8):

.

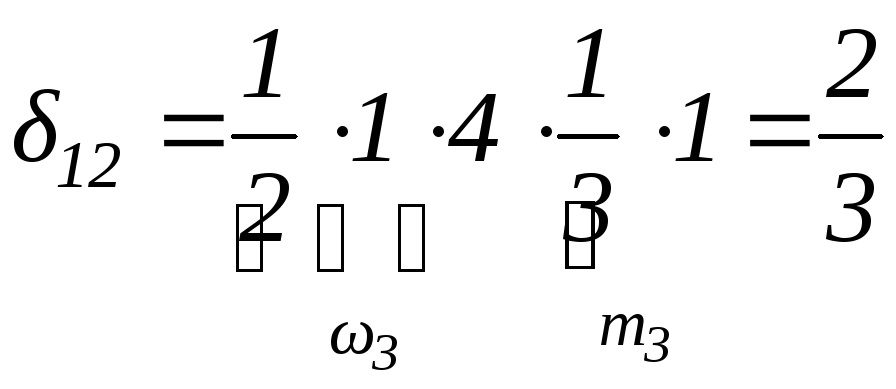Рис.2.8

- эпюру(рис.2.6,д) надо «умножить» на(рис.2.6,в):

.

.

- эпюрунадо «умножить» саму на себя (рис.2.9):

.

Рис.2.9

- эпюру(рис.2.6,д) надо «умножить на(рис.2.6,г):

.

Решаем систему

Умножаем верхнее уравнение на 5и вычитаем нижнее

20Х₁ + 5Х₂ = – 960

– Х₁ – 5Х₂ = – (–231)

19Х₁ = – 729

Получим Х₁ = –38,37 кН∙м, Х₂ = –38,53 кН∙м.

Чтобы найти опорные реакции, рассмотрим последовательно каждую балку из основной системы под действием заданной внешней нагрузки и найденных опорных моментов (рис.2.10)

Рис.2.10

∑М_А = 0; – q ∙ 4 ∙ 2 + R′_B ∙ 4 – 38,4 = 0;

∑у = 0; R_A – q ∙ 4 + R′_B = 0; R_A = 24 ∙ 4 – 57,6 = 38,4 кН.

∑М_В = 0; – q ∙ 4 ∙ 2 + 38,4 + R′_С ∙ 4 – 38,5 = 0;

∑у = 0; R′′_В – q ∙ 4 + R′_С = 0; R′′_В = 24 ∙ 4 – 48 = 48 кН

∑М_С = 0; 38,5 – Р ∙ 3 + R_D ∙ 6 = 0;

∑у = 0; R′′_С – Р + R_D = 0; R′′_С = 40 – 13,6 = 26,4 кН

Реакции опор:

R_A = 38,4 кН; R_В = R′_B + R′′_B = 57,6 + 48 = 105,6 кН;

R_С = R′_С + R′′_С = 48 + 26,4 = 74,4 кН; R_D = 13,6 кН.

Статическая неопределенность раскрыта, далее строим эпюры Q и М(рис.2.11). При этом не составляем аналитические выражения дляQ и Мпо участкам, а пользуемся упрощённой методикой, изложенной в п.5.3 первой части курса.

Из рис.2.11 видно, что в неразрезных балках изгибающий момент на опорах примерно равен (а зачастую и больше) изгибающему моменту в пролёте. Именно поэтому у большинства Санкт-Петербургских мостов через Неву высота сварной балки (или фермы) на опорах больше, чем в пролёте (Троицкий и Литейный мосты).

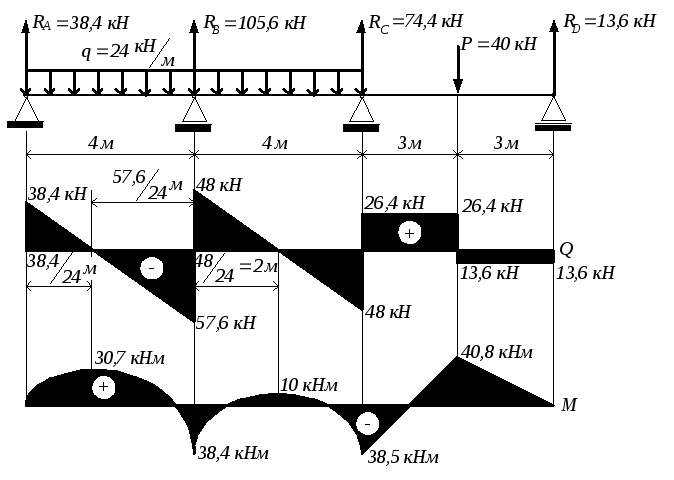
Рис.2.11