KonspLektsy

входных переменных, причем переменная входит со знаком отрицания, если ее

значение равно «1». Далее полученные дизъюнкции перемножаются.

Запишем СКНФ для рассматриваемого мажоритарного элемента:

y (x3 x2 x1)(x3 x2 x1)(x3 x2 x1)(x3 x2 x1)

Любая функция имеет единственную СДНФ и СКНФ.

4) Числовой способ.

Для представления функций в СДНФ под знаком суммы перечисляются номера минтермов. В нашем случае

y (3,5,6,7).

Для представления функций в СКНФ под знаком произведения перечисляются номера макстермов. В нашем случае

y(0,1,2,4).

1.5Построение комбинационной логической схемы

по заданной функции. Понятие базиса.

Получив запись функции, можно непосредственно перейти к построению логической схемы. Например, построим схему, на выходе которой реализуется функция, заданная алгебраическим выражением

у х 0 х1 х2 x0 х1 х2 x0 x1 х 2 x0 x1 x2

Для построения схемы нам понадобятся три инвертора ( для формирования инверсий входных переменных), четыре трехвходовых конъюнктора (для формирования минтермов входных переменных) и один дизъюнктор на четыре входа (для формирования суммы минтермов). Логическая схема имеет вид:

11

	&
1
x0
	&
1	1	y
x1
	&
1
x2	&
	Рис. 1.5

Подобным образом можно строить схемы для любых логических функций, заданных как в ДНФ, так и в КНФ. Отличие состоит только в количестве логических элементов, числе их входов и порядке соединения.

Таким образом, набор из трех логических элементов (И, ИЛИ, НЕ) является достаточным для построения любой логической схемы. Система логических элементов, позволяющая на их основе строить логические схемы любой сложности, называется базис или функционально полная система логических элементов. Так, система, состоящие из элементов И, ИЛИ, НЕ, является базисом.

Однако, согласно принципу двойственности функцию И можно всегда заменить на функцию ИЛИ и наоборот. Поэтому набор из двух элементов (НЕ и И, НЕ и ИЛИ) также будет базисом.

Кроме того, существуют элементы, которые являются базисом сами по себе. Такие элементы называют универсальными. Рассмотрим два таких элемента: ИЛИ-НЕ и И-НЕ.

1.Элемент ИЛИ-НЕ реализует логическую функцию отрицания дизъюнкции

12

у х1 х2 ;

Условное графическое обозначение элемента ИЛИ-НЕ и его таблица

истинности показаны на рис. 1.6.
x	1		1			y	х2	х1	y
x2
							0	0	1
							0	1	0
							1	0	0
							1	1	0

Рис. 1.6

2. Элемент И-НЕ реализует логическую функцию отрицания

	конъюнкции у х1						х2
	Условное графическое обозначение элемента И-НЕ и его таблица
истинности показаны на рис. 1.7.
x1		&
				y			х2		х1	y
x2
							0		0	1
							0		1	1
							1		0	1
							1		1	0

Рис. 1.7

Покажем универсальность элементов ИЛИ-НЕ и И-НЕ. Для этого реализуем с помощью этих элементов три основные логические операции (рис. 1.8):

функция «НЕ»

x

x

&

y x 1 x

1

y x 0 x

“1”

“0”

13

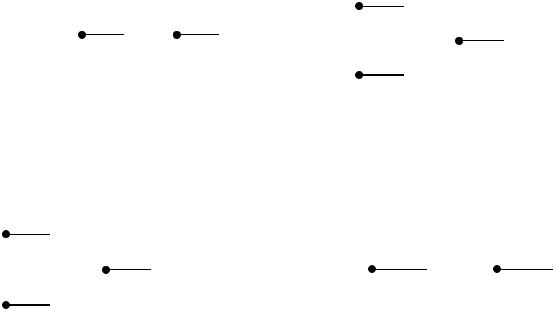
функция «И»

x1

x1

x1

x1x2

1

x1x2

&

&

1

x1 x2 x1 x2

x2

1

x2

x2

функция «ИЛИ»

x1

x1

&

x1

x1 x2

&

x1 x2 x1 x2

1

x x

1

1

2

&

x2

x2

x2

Рис. 1.8

Таким образом, рассмотренный нами способ построения логической схемы не является удовлетворительным, т.к. мы использовали избыточную по своей полноте систему логических элементов. На практике стараются строить схему на элементах одного типа. Кроме того, нами не рассматривался вопрос об оптимизации схемы с точки зрения минимума элементов.

1.6 Минимизация логических функций. Приведение логической

функции к виду, удобному для реализации в заданном

логическом базисе.

После получения алгебраического выражения функцию минимизируют.

Самым очевидным является алгебраический способ, т.е. упрощение функции с использованием законов алгебры логики.

14

Рассмотрим пример, взяв за основу функцию, записанную в ДНФ.

y x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1 x3 x2 x1x2 x1 (x3 x3 ) x3 x1 (x2 x2 ) x3 x2 (x1 x1) x2 x1 x3 x1 x3 x2

Таким образом, получили упрощенную логическую функцию. Однако алгебраический способ требует определенных навыков. Для минимизации разработаны специальные формализованные методы. Рассмотрим минимизацию логических функций с использованием карт Карно.

Карта Карно – таблица, имеющая ячейки для всех возможных значений логической функции. Каждая клетка карты Карно соответствует определенной строке таблицы истинности.

Пусть функция двух переменных задана таблицей истинности

х2	х1	у
0	0	1
0	1	1
1	0	0
1	1	0

Карта Карно для такой функции будет выглядеть следующим образом.

x1

x2

0 1

0 1 1

1 0 0

Значение переменной х2 откладывается по вертикали, а значение переменной х1 – по горизонтали. В каждую клетку записывается значение функции, соответствующее заданной комбинации входных переменных.

15

Кодирование клеток должно отвечать условию: соседние клетки должны отличаться значением лишь одной логической переменной. Соседние клетки соответствуют соседним минтермам.

Минимизация возможна, когда единицы находятся в соседних клетках. При этом образуется контура склеивания, которые составлены из соседних единиц. В контур могут объединяться 1, 2 , 4, 16, 32 клетки (большее количество клеток не используют в этом методе), т.е. количество клеток, равное

2n . Для каждого контура записывается контерм или элементарная конъюнкция, в которую не входят переменные, меняющие значения на этом контуре. В нашем примере переменная х1 меняет свое значение в пределах контура с нуля на единицу, поэтому ее не записываем в выражение для выходной функции. Переменная х2 не изменяет свое значение в пределах контура (равна 0), поэтому ее записываем в выражение для выходной функции

(а поскольку ее значение – нуль, то записываем переменную как инверсную). В

результате

	x1	0	1
	x2
				у х2
	0
		1	1

1 0 0

Рис.1.9

Правила минимизации:

Все клетки с единицами на карте Карно должны быть обведены контурами, допустимое количество клеток в контуре – 2n, n = 0,1,2…

Размеры контуров должны быть максимальными, а количество контуров – минимальным.

Допускается взаимное пересечение контуров.

Рассмотрим минимизацию функции трех переменных. Карта Карно для такой функции получается зеркальным отображением вправо карты Карно для функции двух переменных. В этом случае по горизонтали откладываются

16

значения переменных х2х1. При этом в левой полуплоскости карты переменная

х2 = 0, а в правой полуплоскости х2 = 1. Нарисуем карту Карно трех переменных и пронумеруем ее клетки. Номер клетки соответствует номеру строки таблицы истинности.

x2x1	00		01	11	10
x3
0
		0	1	3	2
1
		4	5	7	6

Правила минимизации остаются те же, но появляется дополнительная возможность склеивания относительно оси симметрии. Образование контуров продолжается, пока все единицы не поучаствуют в процессе склеивания. Для каждого контура записывается контерм (элементарная конъюнкция), далее образуется сумма контермов для всех контуров: В качестве примера рассмотрим карту Карно, в которой выделим два контура:

x2x1	00	01	11		10
x3									1 контур: х1
0	1	0		0		1		2	2 контур:				х3 х2
1	1	0		1		1			у х1 х3			х2
			1
					Рис 1.10

Карта Карно для функции четырех переменных получается зеркальным отображением вниз карты Карно для функции трех переменных. В этом случае по горизонтали откладываются значения переменных х2х1, а по вертикали – переменные х4х3, причем в верхней полуплоскости карты переменная х4 = 0, а в нижней полуплоскости х4 = 1. Появляется дополнительная возможность склеивания относительно второй оси симметрии. В показанной ниже карте Карно имеются три контура (1 контур: клетки 10, 11, 14, 15; 2 контур: клетки 0,

17

2, 8,10; 3 контур: клетка 5). Контур, содержащий только одну единицу,

называется вырожденным.

x2x1	00	01	11	10
x4x3
00
	1	0	0	1
						y x4	x2	x3 x1 x4 x3 x2 x1
01
	0	1	0	0
11
	0	0	1	1
10
	1	0	1	1
					Рис. 1.11

Карта Карно для функции пяти переменных получается зеркальным отображением вправо карты Карно для функции четырех переменных. Карта Карно для функции шести переменных получается зеркальным отображением вниз карты Карно для функции пяти переменных. Для большего числа переменных, как правило, применяются другие способы минимизации.

После минимизации функции переходим к определенному базису. Пусть в результате минимизации получена функция

y x3 x2 x3 x1 x2 x1

Чтобы перейти к базису «И – НЕ», необходимо преобразовать функцию y

так, чтобы в нее входила только операция «И – НЕ». Для этого дважды проинвертируем функцию y:

y x3x2 x3x1 x2 x1 (x3x2 ) (x3x1) (x2 x1)

Логическая схема, на выходе которой реализуется данная функция:

18

x1 &

x2

&

& y

x3 &

Рис.1.12

Чтобы перейти к базису «ИЛИ – НЕ», воспользуемся правилом

х2 х1 х2 х1

Тогда

у (х3 х2 ) (х3 х1) (х2 х1)

Результирующая функция является функцией «ИЛИ». Чтобы получить функцию «ИЛИ – НЕ», проинвертируем левую и правую части выражения.

у (х3 х2 ) (х3 х1 ) (х2 х1 )

Схема в базисе «ИЛИ – НЕ»:

х1

1

				1			1
х2
									у
				1

х3

Рис 1.13

19

		1.7 Особенности минимизации логической функции при
				наличии факультативных условий
Рассмотрим пример. Пусть требуется построить схему выделения четного
числа в пределах 10. Необходимое число входных переменных для
формирования 10 значений функции – четыре (24 = 16). Тогда логическую
функцию можно записать в виде:
y об (0,2,4,6,8) ф (10,11,12,13,14,15) ,
где об - обязательные условия
ф - факультативные условия
(0,2,4,6,8) - номера минтермов, на которых значение функции равно 1.
(10,11,12,13,14,15) - номера минтермов, на которых значение функции не
определено.
Для более полной минимизации производят доопределение логической
функции. Для факультативных условий можно задать произвольное значение
таким образом, чтобы образовать контура максимальной размерности.
x4 x3					Если в контура объединить только клетки с
x2 x1	00	01	11	10	единицами, то получим два контура	(1
00	1 0	1 4	×=112	1 8	контур: клетки 0, 2, 4, 6; 2 контур: клетки 0
01	0 1	05	×=013	0 9	и 8). Выходная функция в этом случае
11	0 3	0 7	=0	=0	у х4 х1 х3 х2 х1
			× 15	× 11
10	1 2	1 6	×=114	×=110	Доопределим факультативные состояния	в
					клетках с номерами 10, 12 и 14 единицами, а
Рис.1 14

в клетках 11, 13 и 15 – нулями. Тогда получаем только один большой контур

(клетки вхо0, 2, 4, 6, 8, 10, 12, 14) и выходная функция получится гораздо проще: y x

.

20