KonspLektsy

УрФУ

ЦИФРОВЫЕ УСТРОЙСТВА

Конспект лекций

по дисциплине «Цифровые устройства» для студентов всех форм и технологий обучения

направления подготовки бакалавров

210700 Инфокоммуникационные технологии и системы связи

по дисциплине «Цифровые устройства и микропроцессоры» для студентов всех форм и технологий обучения направления подготовки бакалавров 210400 Радиотехника

Автор: Маевская Е.А.

Екатеринбург

2011 г

1

1. ЦИФРОВЫЕ И ЛОГИЧЕСКИЕ СИГНАЛЫ.

ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ.

1.1 Сигналы цифровых устройств. Логические переменные.

Сигналом называют физический процесс, несущий информацию.

Различают аналоговые и цифровые сигналы. К примеру, сигналы на выходе микрофона или различного рода датчиков аналогичны воздействиям на эти устройства – звуковому давлению, температуре и т.д. Поэтому такие сигналы называют аналоговыми, а устройства, в которых они действуют – аналоговыми

устройствами.

Цифровые сигналы разделяют на две категории:

цифровые эквиваленты аналоговых сигналов (такой сигнал

формируются из аналогового сигнала и несет в себе всю информацию о численном значении параметров физических величин, заложенную в аналоговом сигнале: о температуре,

давлении, напряжении и т.д.);

логические сигналы (такие сигналы несут информацию о наступлении или ненаступлении какого-либо события).

Устройства, в которых действуют цифровые сигналы, называют цифровыми устройствами. При описании функционирования таких устройств и при их проектировании используют математический аппарат алгебры логики.

Алгебра логики – это формальный аппарат описания логической стороны процессов в цифровых устройствах. По имени автора этого математического аппарата английского математика Джорджа Буля его называют булевой алгеброй.

Булева алгебра имеет дело с логическими переменными, которые могут принимать только 2 значения: ИСТИНА и ЛОЖЬ, TRUE и FALSE, ДА и НЕТ, 1

и 0. Наиболее распространено последнее обозначение. Необходимо отметить,

2

что применительно к логическому сигналу символы 0 и 1 никакого отношения к числовому значению сигнала не имеют. Они лишь описывают качественное состояние события, и поэтому к ним неприменимы арифметические операции.

В электрических цепях эти символы представляются двумя уровнями напряжения: высоким, близким к Uпит, и низким, близким к нулю. Это так называемая потенциальная система представления информации. Два уровня,

характеризующие логические состояния, определяются просто как более высокий – H (high) и низкий – L (low). Эти 2 значения называют логическими уровнями.

Существуют два рода так называемых логических соглашений в зависимости от того, каким уровнем напряжения кодировать логическую 1 (и

соответственно логический 0). В соглашении положительной логики более высокий уровень соответствует логической 1, а низкий – логическому 0. В

соглашении отрицательной логики – наоборот. Соглашение положительной логики имеет преимущественное применение.

Логические переменные хорошо описывают состояния таких элементов,

как реле, тумблеры, кнопки и т.п., т.е. таких элементов, которые могут находиться в двух состояниях: включено – выключено. К таким объектам относятся и ПП логические элементы, на выходе которых может быть лишь один из двух уровней напряжения – низкий или высокий.

1.2 Основные соотношения булевой алгебры.

Булева алгебра оперирует с переменными, принимающими только два значения: 0 и 1, т.е. с двоичными переменными. Над такими переменными в булевой алгебре определены три основные операции: конъюнкция, дизъюнкция и инверсия.

1.Конъюнкция (логическое умножение, операция И)

Конъюнкция записывается в виде

y = xn-1 ∙ xn-2 ∙…∙ x0 либо y = xn-1 Λ xn-2 Λ …Λ x0.

3

Элемент, выполняющий операцию конъюнкции, называется конъюнктором или

элементом И. Работает такой элемент следующим образом: на выходе логическая 1 только тогда, когда все входные сигналы единичные. На рис.1.1

показан двухвходовой элемент И (выполняющий конъюнкцию двух переменных) и таблица, описывающая его функционирование. Такая таблица называется таблица истинности. В каждой строке таблицы истинности записывается комбинация входных переменных и соответствующее ей значение функции.

						х1	х0	y
	x1
				y		0	0	0
			&
						0	1	0
	х0					1	0	0
						1	1	1

Рис. 1.1

2. Дизъюнкция (логическое сложение, операция ИЛИ)

Дизъюнкция записывается в виде

y = xn-1 + xn-2 +…+ x0 либо y = xn-1 V xn-2 V …V x0.

Элемент, выполняющий операцию дизъюнкции, называется дизъюнктором или

элементом ИЛИ. Работает такой элемент следующим образом: на выходе логическая 1 тогда, когда хотя бы один из входных сигналов единичный. На рис.1.2 показан двухвходовой элемент ИЛИ и его таблица истинности.

						х1	х0	y
	x1
				y		0	0	0
			1
						0	1	1
	х0					1	0	1
						1	1	1

Рис. 1.2

3. Инверсия (логическое отрицание, операция НЕ)

Инверсия записывается в виде y x .

4

Элемент, выполняющий операцию инверсии, называется инвертором или

элементом НЕ. Условное графическое обозначение элемента НЕ и его таблица истинности показаны на рис.1.3.

	x			y	x	y
			1
					0	1
					1	0

Рис.1.3

В булевой алгебре действует принцип двойственности: операции И и ИЛИ можно поменять местами, если единицу заменить на ноль, ноль на единицу и поменять местами знаки умножения и сложения.

Действительно: 0+0=0 → 1·1=1 1·0=0 → 0+1=1

Основные тождества булевой алгебры:

х 0 х			х 1 1	х х 1				х х х
х 1 х			х 0 0	х х 0				х х х
х х

Основные законы булевой алгебры:

1. коммутативный (переместительный) закон

у х х у;

х у у х

2. ассоциативный (сочетательный) закон

(х у) с х ( у с);

(х у) с х ( у с)

3. дистрибутивный (распределительный) закон

х ( у с) х у х с;

х у с (х у)( х с)

Справедливость последнего равенства (не имеющего аналога в обычной алгебре) легко доказать. Раскроем скобки в правой части равенства

(x y)(x c) x x y x x c y c x (1 y c) y c x y c

5

4.	закон поглощения
	х х у х;					х(х у) х
5.	закон склеивания
	х у х у у;						(х у)( х у) у
6.	закон обобщенного склеивания
	х х у х у;						х(х у) х у

Доказательство:

x y x y (x x) x y x y x x (1 y) y x x y x

x y x ( y x x) x y x x x ( y x)

7.закон отрицания (теорема де Моргана)

ху х у

ху х у

Справедливость этих выражений следует из принципа двойственности.

1.3 Понятие о логической функции и логическом устройстве.

Логическая или булева функция представляет собой логическое выражение, составленное из n логических переменных с помощью конечного числа операций алгебры логики. Задать булеву функцию – это значит указать все ее значения при всех возможных комбинациях значений аргументов.

Каждая конкретная комбинация входных переменных, записанных в определенном порядке (от переменной с большим индексом к переменной с меньшим индексом), представляет собой набор. Каждому набору соответствует свой номер – десятичное число, представляющее данный набор. Например,

набору трех переменных 101 соответствует номер 5 (1·20 + 0·21 + 1·22 = 5), а

набору 110 – номер 6.

Логическая функция является полностью определенной, если известно ее значение для каждого набора аргументов. Если хотя бы на одном наборе

6

значение функции неизвестно, то логическая функция является недоопределенной или частично определенной.

Устройства, предназначенные для формирования логических функций,

называют логическими устройствами или цифровыми устройствами. Типовые каскады логических устройств подразделяют на собственно логические элементы и элементы памяти. Собственно логические элементы осуществляют преобразование логических сигналов, а элементы памяти – запоминание информации.

По способу функционирования логические устройства (и их схемы) делят на два класса: комбинационные устройства (и соответственно комбинационные схемы) и последовательностные устройства (последовательностные схемы).

Комбинационные устройства (называемые также автоматами без памяти)

состоят только из логических элементов. В таких устройствах сигнал на выходе определяется только комбинацией входных сигналов в данный момент времени.

Последовательностные устройства кроме логических элементов содержат также элементы памяти. В таких устройствах (или автоматах с памятью)

выходной сигнал определяется не только комбинацией входных сигналов в данный момент времени, но и внутренним состоянием устройства, а последнее зависит от того, какие сигналы действовали на входах во все предшествующие моменты времени в процессе работы устройства. Поэтому в отличие от комбинационных устройств последовательностные устройства обладают памятью (они хранят сведения о прошлом работы устройства).

7

Рассмотрим примеры комбинационного и последовательностного устройства. Пусть устройство (рис.1.4,а) предназначено для формирования на выходе сигнала, определяющего совпадение сигналов на входах (f=1 при x1=x2

и f=0 при х1 х2). Такое устройство является комбинационным, в котором значения формируемой на выходе логической функции определяется лишь значениями ее аргументов в данный момент времени.

х1
	Комбинационное	f (х1, x2)	Вх.	Последовательностное
				устройство
	устройство				Вых.
х2

							Вх.
х1	1	0	0	1	1	0
							0	1	0	01	0	1	0
	1	1	0	1	0	0							t
х2
						Вых	0	0	1	1	0	0	1
													t
f(x1, x2)	1	0	1	1	0	1
							0	0	0	0	1	1	1
													t

a)

б)

Рис.1.4

Рассмотрим другой пример. Счетчик на рис.1.4,б подсчитывает импульсы.

В каждый момент времени его состояние соответствует числу поступивших на вход импульсов. Выходная информация определяется тем, каково было состояние счетчика до данного интервала времени и поступает или нет на вход импульс в данном интервале времени. Таким образом, данное устройство является последовательностным.

8

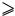
1.4Способы задания логических функций.

1)Словесное описание функционирования логической схемы.

Например, сигнал «1» появляется на выходе логической схемы, если хотя бы два из трех входных сигналов имеют значение «1».

2) Табличный способ.

Эту же функцию можно задать с помощью таблицы истинности. Такие таблицы уже использовались при описании функционирования схем И, ИЛИ и НЕ. Если число аргументов функции равно n, то число различных сочетаний (наборов)

значений аргументов составляет 2n. Поэтому таблица истинности функции n

аргументов будет иметь (n+1) столбцов: n для набора аргументов и один для значения функции на данном наборе, и 2n строк. Составим таблицу истинности для мажоритарного элемента, работу которого мы ранее описали словами.

		M
x0				y	х2	х1	х0	y
x1
					0	0	0	0
x2
					0	0	1	0
					0	1	0	0
					0	1	1	1
					1	0	0	0
					1	0	1	1
					1	1	0	1
					1	1	1	1

3) Алгебраический способ.

Логическая функция записывается в форме логического выражения,

показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции. Существует две формы функций в алгебраическом виде называемых нормальными:

 Дизъюнктивная нормальная форма (ДНФ) или первая форма.

ДНФ – это логическая сумма элементарных логических произведений:

9

у х1х2 х0 х1 .

Если каждое слагаемое содержит все входные переменные в их прямом или инверсном виде, то функция имеет совершенную дизъюнктивную нормальную форму (СДНФ) или первую стандартную форму:

у х1х2 х3 х1х2 х3 .

Каждое из произведений переменных, для которых значение функции равно единице, называется минтермом. Таким образом, СДНФ – логическая сумма минтермов.

Используя таблицу истинности, можно записать функцию в СДНФ. Для этого выделяются строки таблицы истинности, в которых значения логической функции равны «1». Для каждой такой строки записывается конъюнкция входных переменных, причем переменная входит со знаком отрицания, если ее

значение равно «0». Полученные конъюнкции суммируются.

Например, для нашего мажоритарного элемента СДНФ запишется следующим образом:

yx3x2 x1 x3 x2 x1 x3x2 x1 x3x2 x1

Конъюнктивная нормальная форма (КНФ) или вторая форма.

КНФ – это логическое произведение элементарных логических сумм:

у (х0 х1)( х2 х1)

Если каждый сомножитель содержит все входные переменные в их прямом или инверсном виде, то функция имеет совершенную конъюнктивную нормальную форму (СКНФ) или вторую стандартную форму:

у (х0 х1 х2 )( х0 х1 х2 ) .

Каждая из сумм переменных, для которых значение функции равно нулю,

называется макстермом. Таким образом, СКНФ – логическая сумма макстермов.

Используя таблицу истинности, можно записать функцию в СКНФ. Для этого выделяются строки таблицы истинности, в которых значения логической функции равны «0». Для каждой такой строки записывается дизъюнкция

10