
2.5. Импульс, момент импульса.
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. ЗАКОНЫ ИЗМЕНЕНИЯ. ТЕОРЕМЫ СОХРАНЕНИЯ
Уравнения
движения (1.2), (2.2) определяют закон
изменения импульса материальной точки,
из которых следует, что если ![]() ,
то вектор импульса точки
,
то вектор импульса точки ![]() где
где ![]() -
постоянный вектор. Это утверждение
носит характер теоремы. Так как
-
постоянный вектор. Это утверждение
носит характер теоремы. Так как ![]() - трехмерный вектор, то в случае равенства
нулю всех трех компонент силы остаются
неизменными во время движения все три
проекции импульса на неподвижные оси.
Однако из (1.2) следует также, что в случае
равенства
нулю какой-либо
проекции силы на неподвижную ось
соответствующая проекция импульса
сохраняется. Функции
- трехмерный вектор, то в случае равенства
нулю всех трех компонент силы остаются
неизменными во время движения все три
проекции импульса на неподвижные оси.
Однако из (1.2) следует также, что в случае
равенства
нулю какой-либо
проекции силы на неподвижную ось
соответствующая проекция импульса
сохраняется. Функции
![]() (19.2)
(19.2)
являются
тремя первыми независимыми интегралами
движения. Найдем векторное произведение
![]() ,
где
,
где ![]() - радиус-вектор точки. Из (1.2) получим
- радиус-вектор точки. Из (1.2) получим
![]() ,
,
или
![]() , (21.2)
, (21.2)
где![]() - момент импульса точки, а
- момент импульса точки, а ![]() - момент силы. Уравнение (21.2) определяет
закон изменения момента импульса точки
со временем. Из (21.2) следует теорема:
- момент силы. Уравнение (21.2) определяет
закон изменения момента импульса точки
со временем. Из (21.2) следует теорема:
Если
вектор момента силы в любой момент
времени равен нулю
![]() ,
то момент импульса точки не изменяется
во время движения, т. е.
,
то момент импульса точки не изменяется
во время движения, т. е.
![]() ,
или по компонентам
,
или по компонентам ![]() .
.
В
случае равенства нулю какой-либо проекции
момента силы соответствующая проекция
момента импульса будет оставаться
постоянной. Компоненты вектора ![]() по декартовым осям
по декартовым осям
![]() .
(22.2)
.
(22.2)
Из
(6.1) и (22.2) видно, что ![]() ,
где
,
где
![]() - секторная
скорость точки. Поставим общий вопрос:
в каких случаях
- секторная
скорость точки. Поставим общий вопрос:
в каких случаях ![]() ,
т. е. когда
,
т. е. когда ![]() является интегралом движения? Оказывается,
это будет в двух случаях: 1)
является интегралом движения? Оказывается,
это будет в двух случаях: 1) ![]() ;
2)
;
2) ![]() .
Первый случай
тривиален, так как на точку не действуют
силы. Во втором случае линия действия
параллельна (или антипараллельна)
радиус-вектору частицы и проходит через
некоторую неподвижную точку-центр силы.
Очевидно, центр силы находится в начале
координат. Тогда
.
Первый случай
тривиален, так как на точку не действуют
силы. Во втором случае линия действия
параллельна (или антипараллельна)
радиус-вектору частицы и проходит через
некоторую неподвижную точку-центр силы.
Очевидно, центр силы находится в начале
координат. Тогда ![]() .
Силы вида
.
Силы вида ![]() называются центральными.
называются центральными.
Таким образом, момент импульса точки относительно центра силы сохраняется. Однако между тремя проекциями момента импульса имеется зависимость, так как
![]() , (23.2)
, (23.2)
![]() .
(24.2)
.
(24.2)
Аналогично
![]() (25.2)
(25.2)
Но
если ![]() ,
то
,
то ![]() ,
и, следовательно
,
и, следовательно
![]()
![]() .
(26.2)
.
(26.2)
Из
(26.2) видим, что под действием центральной
силы точка движется по плоской траектории,
плоскость которой проходит через центр
силы и перпендикулярна постоянному
моменту импульса точки![]() .
.
Заметим, что существование зависимостей (24.2), (25.2) связано с невозможностью решения системы линейных уравнений
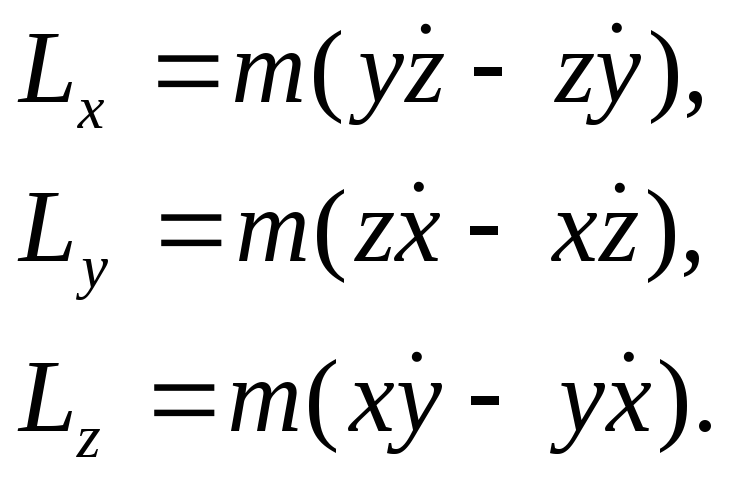 (27.2)
(27.2)![]()
как
относительно ![]() (при
фиксированных
(при
фиксированных ![]() ),
так и относительно
),
так и относительно ![]() (при
фиксированных
(при
фиксированных ![]() ).
Легко проверить, что функциональный
определитель этой системы равен нулю.
).
Легко проверить, что функциональный
определитель этой системы равен нулю.
Вычислим
скалярное произведение векторов ![]() и
и ![]() ,
умножая (2.2) скалярно на вектор
,
умножая (2.2) скалярно на вектор ![]() :
:
![]() .
(28.2)
.
(28.2)
Левая часть (28.2) равна полной производной по t от кинетической энергии точки
![]() .
(29.2)
.
(29.2)
Правая часть (28.2) равна мощности силы. Рассмотрим случай потенциальной силы. Силу называют потенциальной, если она зависит только от координат и времени и удовлетворяет векторному уравнению
![]() .
(30.2)
.
(30.2)
Если
(30.2) выполняется, то ![]() можно представить в виде
можно представить в виде
![]() ,
(31.2)
,
(31.2)
скалярную
функцию U
называют
потенциальной энергией точки. Пусть ![]() и
и ![]() не зависят
от
не зависят
от ![]() явно. Используя
(31.2), представим
явно. Используя
(31.2), представим ![]() в виде
в виде
![]() . (32.2)
. (32.2)
Выражая
![]() из (29.2) и подставляя полученное, а также
(32.2) в (28.2), находим
из (29.2) и подставляя полученное, а также
(32.2) в (28.2), находим
![]() . (33.2)
. (33.2)
Здесь
![]() - элементарная
работа потенциальной силы, т. е.
- элементарная
работа потенциальной силы, т. е.![]() .
Так как
.
Так как ![]() и
и ![]() являются в
данном случае полными дифференциалами,
то
являются в
данном случае полными дифференциалами,
то
![]() , (34.2),
, (34.2),
т. е.
![]() .
(35.2)
.
(35.2)
Мы
получили закон сохранения полной
механической энергии точки, которая
определяется как сумма ее кинетической
и потенциальная энергии. Если ![]() и
и ![]() зависят явно от
зависят явно от ![]() ,
то
,
то
![]() .
(36.2)
.
(36.2)
Выражая
отсюда ![]() и подставляя в (28.2), получим
и подставляя в (28.2), получим
![]() .
(37.2)
.
(37.2)
Это закон изменения полной механической энергии точки, движущейся в поле потенциальной силы.
В
задачах механики помимо потенциальных
сил рассматривают также диссипативные
и гироскопические силы. Диссипативная
сила ![]() направлена всегда противоположно
скорости тела относительно среды,
вызывающей торможение тела:
направлена всегда противоположно
скорости тела относительно среды,
вызывающей торможение тела:
![]() ,
(38.2)
,
(38.2)
причём
![]() в общем случае является положительной
скалярной функцией координат и скорости
точки. Гироскопическая сила представима
в виде
в общем случае является положительной
скалярной функцией координат и скорости
точки. Гироскопическая сила представима
в виде
![]() , (39.2)
, (39.2)
где
![]() - скорость точки. Из (39.2) следует, что
вектор
- скорость точки. Из (39.2) следует, что
вектор ![]() ортогонален
вектору скорости
ортогонален
вектору скорости![]() ,
т. е.
,
т. е. ![]() .
Если
.
Если ![]()
![]() и
и ![]() ,
то эти силы нужно учитывать в уравнениях
движения. В частности, закон изменения
полной энергии точки при наличии
потенциальных, гироскопических и
диссипативных сил имеет вид
,
то эти силы нужно учитывать в уравнениях
движения. В частности, закон изменения
полной энергии точки при наличии
потенциальных, гироскопических и
диссипативных сил имеет вид
![]() .
(40.2)
.
(40.2)
1Здесь мы имеем в виду силы, которые возникают в результате фундаментальных взаимодействий: ядерных (сильных), электромагнитных или гравитационных.
2Прекрасное изложение темы ИСО можно найти в книгах:ВейнбергС. Гравитация и космология. М.: Мир, 1975,ЛогуновА. А. Лекции по теории относительности и гравитации. М.: Изд-во МГУ, 1985. Здесь мы во многом следуем этим работам.
3Пространства, в которых квадрат
расстояния между точками, характеризуемыми
радиус-векторами![]() ,
определяется формулой
,
определяется формулой
![]()
называют евклидовыми.
