Глава 4 движение в центральном поле

4.1. Общие закономерности

В центрально-симметричном поле сила, действующая на частицу, по абсолютной величине зависит только от :

(1.4)

и направлена в каждой точке вдоль радиуса-вектора . Выше было показано, что в центральном поле сохраняется момент импульса частицы относительно центра поля . Траектория частицы либо проходит через центр поля, если (так как тогда и, следовательно, траектория является прямой, проходящей через точку ) либо лежит целиком в одной плоскости, проходящей через центр поля и перпендикулярной постоянному вектору . Действительно, так как

, (2.4)

то . Учитывая, что , получим уравнение плоскости, в которой лежит траектория, в явном виде:

. (3.4)

Как было показано в 2.3, общее решение динамической задачи должно зависеть от шести независимых постоянных интегрирования, которыми определяются шесть интегралов движения (три первых и три вторых интеграла)¹. В качестве трех независимых первых интегралов движения можно выбрать полную энергию частицы

(4.4)

и любые две проекции момента импульса . Три первых интеграла не являются независимыми, поэтому мы берем только два из трех. Одним из вторых интегралов движения является соотношение (3.4), так как оно не содержит скоростей частицы и следует из уравнений движения.

Направим ось Oz декартовой системы координат по вектору и далее будем определять положение точки в плоскости орбиты полярными координатами и (рис. 1.4). В цилиндрической системе координат интегралы энергии и момента импульса запишем в виде

, (5.4)

, (6.4)

где .

Выражая через из (6.4) и подставляя в (5.4), получим

. (7.4)

Отсюда

(8.4)

или, разделяя переменные и интегрируя, находим

. (9.4)

Здесь - постоянная интегрирования, а само соотношение есть еще один второй интеграл.

Последний второй интеграл найдем, исключив t из (6.4), (8.4):

. (10.4)

Разделяя в (10.4) переменные и интегрируя, получим

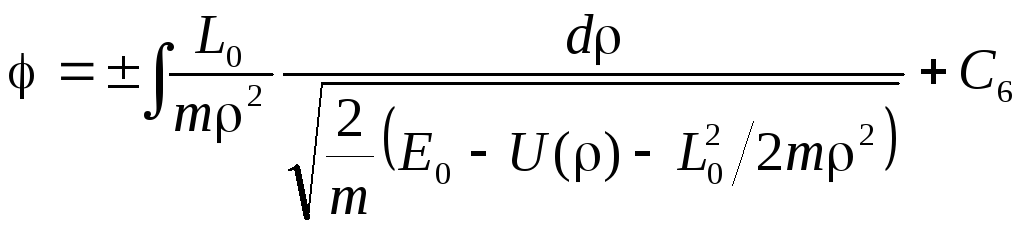. (11.4)

Это соотношение является вторым интегралом движения; оно определяет связь и , т. е. представляет уравнение траектории. Формулой (9.4) определяется в неявном виде функция . Если эта функция найдена, то, подставляя ее в (6.4) и интегрируя (6.4) по времени, получим ()

. (12.4)

Из (7.4) видно, что радиальную часть движения в центральном поле можно рассматривать как одномерное движение в поле с «эффективной» потенциальной энергией

(13.4)

в области . Величину называют центробежной энергией. Границы области движения частицы в радиальном направлении определяются действительными корнями уравнения

. (14.4)

В этих точках , но , так что частица не останавливается (как при настоящем одномерном движении), а продолжает движение со скоростью . Это точки поворота траектории. В них функция меняет знак, а переходит от уменьшения к увеличению и наоборот.

Если уравнение (14.4) имеет корень , а область допустимого движения ограничена лишь условием (рис.2.4), то движение частицы инфинитно – она приходит из бесконечности и уходит на бесконечность. В случае, когда начальное состояние удовлетворяет условию (рис. 3.4), область изменения координаты частицы с энергией имеет две границы. Движение финитно, а траектория в общем случае целиком находится внутри кольца, ограниченного окружностями и (рис. 4.4).

(Здесь рисунки)

Угол поворота радиуса-вектора за время, в течение которого меняется от до и затем до равен

(15.4)

Если , где целые числа, то траектория не замкнута, хотя движение финитно. За бесконечное время траектория бесконечное число раз пройдет через точки и и заполнит все кольцо. Траектория будет замкнутой, если . Ее замыкание произойдет через повторений периода времени, при котором меняется от до и затем до . Радиус-вектор частицы сделает при этом полных оборотов. Из (15.4) видно, что , как и условие замкнутости траектории, зависит от начальных условий ( и ). Только в двух типах центральных полей, независимо от начальных условий, траектории всех финитных движений замкнуты. Это поля, в которых потенциальная энергия частицы равна либо , либо .

Резюмируя, сформулируем следующие из нашего рассмотрения общие свойства движения, справедливые для любого центрального поля:

1) траектория лежит в неподвижной плоскости, проходящей через центр поля, а радиус-вектор частицы описывает равные площади за равные промежутки времени (постоянство или );

2) угол меняется монотонно со временем;

3) траектория точки симметрична относительно апсидальных векторов (прямых, проходящих через центр силы и «точку поворота»).