
- •11.Вероятность появления хотя бы одного события.
- •32. Понятие двумерной случайной величины и закон ее распределения.
- •45.Выборочная дисперсия и ее свойства;
- •48.Точечная оценка математического ожидания
- •49.. Точечная оценка для дисперсии
- •50. Несмщенная точечная оценка генеральной совокупности.
- •53. Интервальная оценка мат.Ожидания
- •56- Методика проверки статистических гипотез
- •57. Критерий согласия Пирсона
- •58. Критерий согласия Колмагорова
- •59. Системы массового обслуживания.
- •60. Основные понятия теории графов.
32. Понятие двумерной случайной величины и закон ее распределения.
Зачастую
результат опыта описывается несколькими
случайными величинами:
 .В
этом случае говорят о многомерной
случайной величине
.В
этом случае говорят о многомерной
случайной величине или о системе случайных величин
или о системе случайных величин .Рассмотрим
двумерную случайную величину
.Рассмотрим
двумерную случайную величину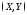 ,
возможные значения которой есть пары
чисел
,
возможные значения которой есть пары
чисел .
Геометрически двумерную случайную
величину можно истолковать как случайную
точку на плоскости
.
Геометрически двумерную случайную
величину можно истолковать как случайную
точку на плоскости .Если
составляющиеХ
и Y
– дискретные случайные величины, то
.Если
составляющиеХ
и Y
– дискретные случайные величины, то
 - дискретная двумерная случайная
величина, а еслиХ
и Y
–
непрерывные, то
- дискретная двумерная случайная
величина, а еслиХ
и Y
–
непрерывные, то
 - непрерывная двумерная случайная
величина.Законом распределения
вероятностей двумерной случайной
величины называют соответствие между
возможными значениями и их
вероятностями.закон распределения
двумерной дискретной случайной величины
может быть задан в виде таблицы с двойным
входом (см. таблица 6.1), где
- непрерывная двумерная случайная
величина.Законом распределения
вероятностей двумерной случайной
величины называют соответствие между
возможными значениями и их
вероятностями.закон распределения
двумерной дискретной случайной величины
может быть задан в виде таблицы с двойным
входом (см. таблица 6.1), где - вероятность того, что составляющаяХ
приняла значение xi,
а составляющая Y
– значение yj.
- вероятность того, что составляющаяХ
приняла значение xi,
а составляющая Y
– значение yj.
33.
Закон
распределения двумерной случайной
величины
 можно
задать в виде функции
распределения
можно
задать в виде функции
распределения
 ,
определяющей для каждой пары чисел
,
определяющей для каждой пары чисел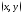 вероятность
того, чтоХ
примет значение, меньшее х,
и при этом Y
примет значение, меньшее y:
вероятность
того, чтоХ
примет значение, меньшее х,
и при этом Y
примет значение, меньшее y:
 .
Геометрически
функция
.
Геометрически
функция
 означает вероятность попадания случайной
точки
означает вероятность попадания случайной
точки в
бесконечный квадрат с вершиной в точке
в
бесконечный квадрат с вершиной в точке Отметим
свойства
Отметим
свойства
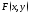 .
.
1.
Область значений функции
 -
- ,
т.е.
,
т.е. .
.
2.
Функция
 - неубывающая функция по каждому
аргументу.
- неубывающая функция по каждому
аргументу.
3. Имеют место предельные соотношения:
 ;
;
 ;
; ;
; .
.
При
 функция
распределения системы становится
равной функции распределения составляющейХ,
т.е.
функция
распределения системы становится
равной функции распределения составляющейХ,
т.е.
Зная
 ,
можно найти вероятность попадания
случайной точки
,
можно найти вероятность попадания
случайной точки в
пределы прямоугольникаABCD
в
пределы прямоугольникаABCD
34.Для двумерной непрерывной случайной величины вводится понятие плотности вероятности
 .
.
Геометрическая
плотность вероятности
 представляет
собой поверхность распределения в
пространстве
представляет
собой поверхность распределения в
пространстве
Двумерная плотность вероятности обладает следующими свойствами:
1.

2.

3.
Функция распределения
 может быть выражена через
может быть выражена через по формуле
по формуле
 .
.
4.
Вероятность попадания непрерывной
случайной величины
 в
область
в
область равна
равна
 .
.
5.
В соответствии со свойством (4) функции
 имеют
место формулы:
имеют
место формулы:


 (6.1.8)
(6.1.8)

35. Условные законы распределения
По
аналогии с условными вероятностями
вводятся условные законы распределения
составляющих непрерывной двумерной
случайной величины
 ,
а именно
,
а именно
 -
условная
плотность распределения Х
при заданном значении
-
условная
плотность распределения Х
при заданном значении
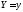 ;
;
 -
условная
плотность распределения Y
при заданном значении
-
условная
плотность распределения Y
при заданном значении
 .
.
Если
случайные величины X
и Y
независимые, т.е. закон распределения
каждой из них не зависит от того, какое
значение принимает вторая величина,
то условные и безусловные законы Х
и Y
совпадают. В частности,
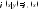 и
и .
Таким образом, для независимых
составляющихХ
и Y
двумерная плотность вероятности
находится следующим образом
.
Таким образом, для независимых
составляющихХ
и Y
двумерная плотность вероятности
находится следующим образом
 и функция
распределения
и функция
распределения имеет
вид
имеет
вид .
Если
составляющиеХ
и Y
дискретной
случайной величины – независимые
случайные величины, то
.
Если
составляющиеХ
и Y
дискретной
случайной величины – независимые
случайные величины, то
 ,
где
,
где
 ,
, ,
,
36. Числовые характеристики двумерной случайной величины.
При изучении двумерных случайных величин рассматриваются числовые характеристики составляющих:
 ,
,
 ,
, ,
, ,где
,где


(6.2.1)

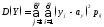 для
дискретных составляющих X
и Y
и
для
дискретных составляющих X
и Y
и


(6.2.2)
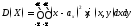
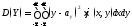 в
случае непрерывных составляющих.
в
случае непрерывных составляющих.
Упорядоченную
пару чисел
 называют математическим ожиданием
двумерной случайной величины, а
называют математическим ожиданием
двумерной случайной величины, а -
ее дисперсия.
-
ее дисперсия.
Отмеченные
выше числовые характеристики не
определяют степень зависимости
составляющих X
и Y.
Эту роль выполняют корреляционный
момент
 (иначе:
ковариация
(иначе:
ковариация ),
который определяется следующим образом:
),
который определяется следующим образом:
 .
(6.2.3)
.
(6.2.3)
Для дискретных случайных величин
 (6.2.4)
(6.2.4)
Для непрерывных случайных величин
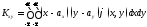 (6.2.5)
(6.2.5)
Корреляционный момент можно вычислить по формуле (6.2.6)
 .
(6.2.6)
.
(6.2.6)
Если
Х и Y
независимы, то
 .
Если
.
Если ,
то Х иY
зависимые случайные величины.
,
то Х иY
зависимые случайные величины.
В
случае
 случайные величиныX
и Y
называют некоррелированными, при этом
она могут быть как зависимыми, так и
независимыми.
случайные величиныX
и Y
называют некоррелированными, при этом
она могут быть как зависимыми, так и
независимыми.
Ковариация
X
и Y
характеризует
не только степень зависимости случайных
величин, но и их рассеяние вокруг точки
 .
Кроме того,
.
Кроме того, -
размерная величина, что затрудняет ее
использование для оценки степени
зависимости для различных случайных
величин.
-
размерная величина, что затрудняет ее
использование для оценки степени
зависимости для различных случайных
величин.
Для оценки зависимости вводится коэффициент корреляции
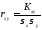 ,
(6.2.7) где
,
(6.2.7) где
 и
и -
среднеквадратические отклоненияX
и Y.
-
среднеквадратические отклоненияX
и Y.
Коэффициент
корреляции
 - безразмерная величина, обладающая
следующими свойствами:
- безразмерная величина, обладающая
следующими свойствами:
1.
 -
ограниченная величина, а именно
-
ограниченная величина, а именно .
.
2.
Если X
и Y
–
независимые случайные величины, то
 .
.
3.
Если X
и Y
связаны
линейной функциональной зависимостью
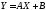 ,
то
,
то и наоборот.
и наоборот.
Из последнего свойства можно сделать вывод: коэффициент корреляции характеризует степень линейной зависимости случайных величин X и Y.
37/ Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.Для непрерывных случайных величин:
где f(y/x) – условная плотность случайной величины Y при X=x.Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y
38. Зависимые и независимые случайные величины. Корреляция
Определение.
Случайная величина X называется независимойот
случайной величины Y если
закон распределения X не
зависит от того, какие значения
приняла Y.Можно
показать, что в этом случае и Y не
зависит от X,
поэтому такие случайные величины часто
называют независимымиТеорема.
Случайные величины X и Y независимы
тогда и только тогда,
когда  .Доказательство.Необходимость.
Пусть X и Y независимы,
а, значит, события X < x и Y < y —
независимы. Тогда для вероятности
произведения независимых событий
имеем
.Доказательство.Необходимость.
Пусть X и Y независимы,
а, значит, события X < x и Y < y —
независимы. Тогда для вероятности
произведения независимых событий
имеем  ,
что и доказывает первое утверждение
теоремы..Определение. Корреляционным
моментом
,
что и доказывает первое утверждение
теоремы..Определение. Корреляционным
моментом
 случайных
величинX и Y называют
случайных
величинX и Y называют  .ЕслиX
= Y,
то есть если понятие корреляционного
момента применить для двух одинаковых
случайных величин, то это будет ни что
иное, как дисперсия. Формулу, записанную
в определении, можно преобразовать к
виду:
.ЕслиX
= Y,
то есть если понятие корреляционного
момента применить для двух одинаковых
случайных величин, то это будет ни что
иное, как дисперсия. Формулу, записанную
в определении, можно преобразовать к
виду: .В
явном виде корреляционный момент
запишется как:
.В
явном виде корреляционный момент
запишется как: —
для дискретных случайных величин;
—
для дискретных случайных величин; —
для непрерывных случайных величин.Теорема.
Если случайные величины X и Yнезависимы,
то их корреляционный
момент
—
для непрерывных случайных величин.Теорема.
Если случайные величины X и Yнезависимы,
то их корреляционный
момент  .Доказательство.Если X и Yнезависимы,
то случайные величины X -
MX и Y -
MY тоже
независимы. Тогда, используя свойства
математического ожидания, получаем:
.Доказательство.Если X и Yнезависимы,
то случайные величины X -
MX и Y -
MY тоже
независимы. Тогда, используя свойства
математического ожидания, получаем: .Теорема
доказана.Если случайные величиныX и Yимеют
размерность, то корреляционный момент
также будет иметь размерность, равную
произведению размерностей каждой из
величин X и Y.
Часто используют другую характеристику
взаимосвязи двух случайных величин,
называемую коэффициент
корреляции.Определение. Коэффициентом
корреляции
.Теорема
доказана.Если случайные величиныX и Yимеют
размерность, то корреляционный момент
также будет иметь размерность, равную
произведению размерностей каждой из
величин X и Y.
Часто используют другую характеристику
взаимосвязи двух случайных величин,
называемую коэффициент
корреляции.Определение. Коэффициентом
корреляции
 случайных
величинX и Y называют
отношение корреляционного момента к
произведению дисперсий каждой из
случайных величин:
случайных
величинX и Y называют
отношение корреляционного момента к
произведению дисперсий каждой из
случайных величин:  .Определенный
таким образом коэффициент корреляции
оказывается всегда безразмерным и,
таким образом не зависит от выбора
системы единиц при измерении случайных
величин. Очевидно, что доказанная выше
теорема справедлива и для коэффициента
корреляции.Теорема. Для
корреляционного момента справедливо
неравенство
.Определенный
таким образом коэффициент корреляции
оказывается всегда безразмерным и,
таким образом не зависит от выбора
системы единиц при измерении случайных
величин. Очевидно, что доказанная выше
теорема справедлива и для коэффициента
корреляции.Теорема. Для
корреляционного момента справедливо
неравенство 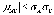 .Доказательство.Рассмотрим
случайную величину
.Доказательство.Рассмотрим
случайную величину  и,
используя свойства математического
ожидания, вычислим дисперсию:
и,
используя свойства математического
ожидания, вычислим дисперсию: .Учитывая,
что дисперсия всегда не отрицательна
.Учитывая,
что дисперсия всегда не отрицательна ,
получаем неравенство
,
получаем неравенство .
Аналогичным образом рассматривая
случайную величину
.
Аналогичным образом рассматривая
случайную величину ,
можно получить, что
,
можно получить, что .
Объединяя эти два неравенства, получаем
.
Объединяя эти два неравенства, получаем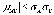 ,
что и доказывает теорему.Следствие. Для
коэффициента корреляции справедливо
неравенство
,
что и доказывает теорему.Следствие. Для
коэффициента корреляции справедливо
неравенство  .Доказательство.
Очевидно из определения коэффициента
корреляции.Определение. Случайные
величины X и Yназывают коррелированными
.Доказательство.
Очевидно из определения коэффициента
корреляции.Определение. Случайные
величины X и Yназывают коррелированными ,
если их корреляционный момент (а, значит,
и коэффициент корреляции) не равен
нулю. Случайные
величины X и Yназывают некоррелированными
,
если их корреляционный момент (а, значит,
и коэффициент корреляции) не равен
нулю. Случайные
величины X и Yназывают некоррелированными ,
если их корреляционный момент (а, значит,
и коэффициент корреляции) равен
нулю.Здесь следует обратить внимание
на неэквивалентность понятий зависимости —
независимости и коррелированности —
некоррелированности. Две коррелированные
случайные величины зависимы, а две
независимые случайные величины —
не коррелированны. Второе из этих
утверждений было доказано выше в одной
из теорем, а первое утверждение можно
доказать, предполагая противное, то
есть если коррелированные величины
независимы, то тогда их корреляционный
момент был бы равен нулю, а, значит, они
были бы не коррелированны. Значит, наше
предположение неверно, что и доказывает
первое утверждение. Напротив, зависимые
случайные величины могут быть
коррелированными (это очевидно, так
как коррелированные величины зависимы),
а могут и не быть таковыми.
,
если их корреляционный момент (а, значит,
и коэффициент корреляции) равен
нулю.Здесь следует обратить внимание
на неэквивалентность понятий зависимости —
независимости и коррелированности —
некоррелированности. Две коррелированные
случайные величины зависимы, а две
независимые случайные величины —
не коррелированны. Второе из этих
утверждений было доказано выше в одной
из теорем, а первое утверждение можно
доказать, предполагая противное, то
есть если коррелированные величины
независимы, то тогда их корреляционный
момент был бы равен нулю, а, значит, они
были бы не коррелированны. Значит, наше
предположение неверно, что и доказывает
первое утверждение. Напротив, зависимые
случайные величины могут быть
коррелированными (это очевидно, так
как коррелированные величины зависимы),
а могут и не быть таковыми.
39. Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:

Любопытно, что ковариация случайной величины с собой равна дисперсии:Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.
Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой
При анализе выборок, содержащих двумерные данные, вычисляется выборочный коэффициент корреляции, который обозначается буквой r. В реальных ситуациях коэффициент корреляции редко принимает точные значения -1, 0 и +1. На рис. 3 приведены шесть диаграмм разброса и соответствующие коэффициенты корреляции rмежду 100 значениями переменных X и Y.
ыборочный коэффициент корреляции:

Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X иY и характеризует степень линейной статистической зависимости величин X и Y и рассеивание относительно точки (mx, my):
Kxy = ,
(11.9)
,
(11.9)
Или

 (11.10)
(11.10)
Расчетные формулы для определения ковариации:
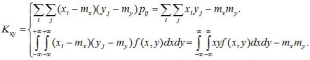 (11.11)
(11.11)
Свойства корреляции:
1. Kxy=Kyx. Это свойство очевидно.
2. Корреляционный момент двух независимых случайных величин Х и У равен нулю.
Доказательство: т.к. случайные величины Х и Y – независимы, то и их совместная плотность распределения представляется произведением плотностей распределения случайных величин fx(x) и fy(y). Тогда:

3. Абсолютная величина корреляционного момента двух случайных величин не превышает среднего геометрического их дисперсий
 или
или 
Доказательство: Введем
в рассмотрение случайные величины 
 и
вычислим их дисперсии
и
вычислим их дисперсии


Т. к. дисперсия всегда неотрицательна, то
 Þ
Þ
и
 Þ
Þ .
.
Отсюда  Þ
Þ .
.
Если  ,
случайные
величиныХ и Y называются коррелированными. Если
,
случайные
величиныХ и Y называются коррелированными. Если  ,
то необязательно, чтоХ иY независимы.
В этом случае они называются некоррелированными. Итак,
из коррелированности двух случайных
величин следует их зависимость, но из
зависимости еще не вытекает их
коррелированность. Из независимости
двух случайных величин следует их
некоррелированность, но из
некоррелированности еще нельзя заключить
о независимости этих величин.
,
то необязательно, чтоХ иY независимы.
В этом случае они называются некоррелированными. Итак,
из коррелированности двух случайных
величин следует их зависимость, но из
зависимости еще не вытекает их
коррелированность. Из независимости
двух случайных величин следует их
некоррелированность, но из
некоррелированности еще нельзя заключить
о независимости этих величин.
Величина
ковариации зависит единиц измерения
каждой из случайных величин, входящих
в систему и от того, насколько каждая
из случайных величин отклоняется от
своего математического ожидания (одна
– мало, вторая – сильно, все равно 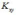 будет
мал).
будет
мал).
Поэтому для характеристики связи между Х и Y в чистом виде переходят к безразмерной характеристике, которая называется Коэффициент корреляции rxy характеризует степень линейной зависимости величин:
 (11.12)
(11.12)
Свойства коэффициента корреляции:
1. Абсолютная
величина коэффициента корреляции двух
случайных величин не превышает единицы: 
2. │rxy│=1 если Y=aХ+b
Доказательство: 
Подставим в выражение

т.к. 
Найдем
дисперсию Y:  ,
т.е.
,
т.е.
 ,
коэффициент корреляции:
,
коэффициент корреляции:  Þ
Þ
Коэффициент корреляции служит для оценки тесноты линейной связи между Х и Y: чем ближе абсолютная величина коэффициента корреляции к 1, тем связь сильнее, чем ближе к 0, тем слабее.
3. Если величины X и Y независимы, то rxy = 0.
40. Линейная регрессия ) — используемая в статистикерегрессионная модельзависимости одной (объясняемой, зависимой) переменнойy от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функциейзависимости.
Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели
42. ВЫБОРОЧНЫЙ МЕТОД - статистический метод исследования общих свойств совокупности к.-л. объектов на основе изучения свойств лишь части этих объектов, взятых на выборку. Общее понятие о выборочном методе. Множество всех единиц совокупности, обладающих определенным признаком и подлежащих изучению, носит в статистике название генеральной совокупности.
На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого является распространение полученных результатов на всю генеральную совокупность, т. е. применяют выборочный метод. свойства совокупности, исследуемые В. м., могут быть качественными и количественными. В первом случае задача выборочного обследования заключается в определении количества М объектов совокупности, обладающих к.-л. признаками (напр., при статистич. контроле часто интересуются количеством М дефектных изделий в партии объема N). Оценкой для М служит отношение mN/n, где m - число объектов с данным признаком в выборке объема n. В случае количественного признака имеют дело с определением среднего значения совокупности x̄ = (x1 + x2 + ... + xN). Оценкой для х̄ является выборочное среднее

где Х1, Х2, ..., Хn - те значения из исследуемой совокупности х1, х2, ..., xN, к-рые принадлежат выборке. С математич. точки зрения первый случай - частная разновидность второго, к-рая имеет место, когда М величин xi равны 1, а остальные (N - M) равны 0; в этой ситуации x̄ = M/N и Х̄ = m/n.
В математич. теории В. м. оценка среднего значения занимает центральное место потому, что она служит основой количественного описания изменчивости признака внутри совокупности, т. к. за характеристику изменчивости обычно принимают дисперсию

представляющую собой среднее значение квадратов отклонений xi от их среднего значения х̄. В случае изучения качественного признака
σ2 = М(N - M)/N2.
Для этого из генеральной совокупности особым образом отбирается часть элементов, так называемая выборка, и результаты обработки выборочных данных (например, средние арифметические значения) обобщаются на всю совокупность.
Теоретической основой выборочного метода является закон больших чисел. В силу этого закона при ограниченном рассеивании признака в генеральной совокупности и достаточно большой выборке с вероятностью, близкой к полной достоверности, выборочная средняя может быть сколь угодно близка к генеральной средней. Закон этот, включающий в себя группу теорем, доказан строго математически. Таким образом, средняя арифметическая, рассчитанная по выборке, может с достаточным основанием рассматриваться как показатель, характеризующий генеральную совокупность в целом.
Разумеется, не всякая выборка может быть основой для характеристики всей совокупности, к которой она принадлежит. Таким свойством обладают лишь репрезентативные (представительные) выборки, т. е. выборки, которые правильно отражают свойства генеральной совокупности. Существуют способы, позволяющие гарантировать достаточную репрезентативность выборки. Как доказано в ряде теорем математической статистики, таким способом при условии достаточно большой выборки является метод случайного отбора элементов генеральной совокупности, такого отбора, когда каждый элемент генеральной совокупности имеет равный с другими элементами шанс попасть в выборку. Выборки, полученные таким способом, называютсяслучайными выборками. Случайность выборки является, таким образом, существенным условием применения выборочного метода
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида: 1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор. 2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.
43. Вариационный ряд
Понятие вариационного ряда. Первичные статистические данные, с которыми имеет дело историк, часто представлены неупорядоченной последовательностью чисел, характеризующей ту или иную сторону процесса или явления. В этой совокупности чисел бывает трудно разобраться, и первичная обработка материалов сводится к приведению имеющихся данных к виду, удобному для анализа. При построении вариационного ряда можно приписывать вариантам не частоты, а рассматривать доли каждой варианты во всей совокупности. Они вычисляются как отношения соответствующих частот к объему всей совокупности и называются частостями (обозначим их qi). Частости могут быть выражены в относительных числах или процентах (см. табл.1).Дискретный и интервальный вариационные ряды. Изменение признака, по которому обследуются объекты, может быть дискретным и непрерывным. Дискретной вариацией признака называется такая, при которой отдельные значения варианты отличаются на некоторую конечную величину. В приведенном примере вариация признака зафиксирована как дискретная (отдельные значения варианты отличаются на единицу). Вариация называется непрерывной, если отдельные значения признака могут отличаться друг от друга на сколько угодно малую величину. Примером непрерывной вариации признака служит распределение посевных площадей по урожайности.В зависимости от вида вариации различают дискретные и интервальные вариационные ряды. Дискретный признак служит основой для построениядискретного ряда (см. табл. 1). В случае непрерывного признака варианты объединяют в интервалы, образуя интервальныйряд.Для того чтобы построить интервальный ряд, после выбора принципа построения нужно определить величину интервала. Величина интервала должна быть такой, чтобы, с одной стороны, ряд не оказался слишком громоздким и, с другой стороны, в нем не исчезали бы особенности изучаемого явления. Величина интервала для ряда с равными интервалами определяется соотношениемh=R/k, где R-размах вариации; k-количество интервалов.Медиана – это значение признака ряда, относительно которого вариационный ряд делится на две равные по числу вариантов части. Ее можно определить также как значение признака, приходящееся на середину ранжированного ряда.
44.
Средняя
арифметическаяСредняя
арифметическая применяется, когда
объем совокупности представляет собой
сумму всех индивидуальных значений
варьирующего признака. Следует отметить,
что если вид средней величины не
указывается, подразумевается средняя
арифметическая. Ее логическая формула
имеет вид:
 Средняя
арифметическая простая рассчитывается по
несгруппированным данным по
формуле:
Средняя
арифметическая простая рассчитывается по
несгруппированным данным по
формуле:
 или
или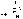 ,
где
,
где –
отдельные значения признака;
j –
порядковый номер единицы наблюдения,
которая характеризуется значением
–
отдельные значения признака;
j –
порядковый номер единицы наблюдения,
которая характеризуется значением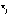 ;
N
– число единиц наблюдения (объем
совокупности).
;
N
– число единиц наблюдения (объем
совокупности).
Наиболее распространенной мерой уровня - является средная арифметическая:

Свойства средней арифметической:
1Если
 ,
то
,
то .
.
2Если всеварианты умножить на одно и то же число, то средняя арифметическая умножается на то же число:

3) Средняя арифметическая отклонений вариант от средней равна нулю.

4)
Средняя арифметическая алгебраической
суммы нескольких признаков равна такой
же сумме средних арифметических этих
признаков: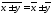
5) Если ряд состоит из нескольких групп, то общая средняя арифметическая равна средней арифметической групповых средних, причем весами являются относительные объемы групп:
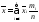
где
 —
групповые средние,
—
групповые средние,
 —объемы
групп,
—объемы
групп,
 —число
групп.
—число
групп.
