48.Точечная оценка математического ожидания

 

Задана случайная величина Х: х₁, х₂, …, х_n, так как М(Х) не найти, то для математического ожидания случайной величины Х естественно предложить среднее арифметическое

 

(1.3)

 

её наблюденных значений.

1. По методу произведений 

, ,

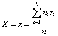так как

.

Это и означает, что оценка несмещенная.

2. Если исследуемая случайная величина Х имеет конечную дисперсию, то эта оценка будет состоятельной, так как

.

Если исследуемая величина имеет нормальный закон распределения, то можно показать, что предложенная оценка эффективна, т. е. оценки для математического ожидания с меньшей дисперсией не существует для нормально распределенных величин.

 Точечная оценка математического ожидания Пустьвыборка из генеральной совокупности, соответствующей случайной величинеx с неизвестным математическим ожиданием Mx =q  и известной дисперсией  .  Рассмотрим оценку неизвестного математического ожидания

.

Оценка несмещённая, поскольку её математическое ожидание равно Mx =q  :

,  Оценка состоятельная, поскольку при n®¥, :

.

Итак, для оценки неизвестного математического ожидания случайной величины будем использовать выборочное среднее: .

49.. Точечная оценка для дисперсии

 

Так как дисперсия определяется через математическое ожидание, а для математического ожидания оценка уже выбрана, то для дисперсии естественно предложить оценку:

 

или ;               (1.4)

 

,                 (1.5)

 

что соответствует записи дисперсии в виде .

Оказывается, что предложенная оценка дисперсии (1.4) состоятельна (легко доказать) и (1.5) не является несмещенной. Чтобы в этом убедиться, возведём в квадрат последнее слагаемое в (1.4)

Процентрируем величину Х, т. е. перенесем начало координат в точку М(Х): . Дисперсия зависит лишь от разности значенийХ и математического ожидания, поэтому от переноса начала координат оценка не изменится и равенство можно продолжить:

.

Вычислим теперь математическое ожидание полученной величины

,

т. е. , так как.

Значит, предложенная оценка занижает истинное значение дисперсии.

Для получения несмещенной оценки введем поправку и полученную оценку обозначим через S²

или

 

                                        .                                        (1.6)

 

Оценка S² (1.6) является состоятельной, так как сходится по вероятности кМ(Х²), а – кМ(Х).

Замечание. При малых n дробь довольно значительно отличается от единицы, а с увеличениемn стремится к единице. При n > 50 практически нет разницы между оценками иS². Оценки и S² являются состоятельными оценками дисперсии.

Для дисперсии случайной величиныможно предложить следующую оценку:

, где — выборочное среднее.

Доказано, что эта оценка состоятельная, но смещенная. В качестве состоятельной несмещенной оценки дисперсии используют величину

.

Именно несмещенностью оценки объясняется ее более частое использование в качестве оценки дисперсии.

50. Несмщенная точечная оценка генеральной совокупности.

Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину

Величина называетсяотносительной частотой значения признака x_i. Если значения признака, полученные из выборки не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой

.

Естественно считать величину выборочной оценкой параметраM. Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.

Выборочную дисперсию

можно считать точечной оценкой дисперсии D генеральной совокупности.

Приведем еще один пример точечной оценки. Пусть каждый объект генеральной совокупности характеризуется двумя количественными признаками x и y. Например, деталь может иметь два размера – длину и ширину. Можно в различных районах измерять концентрацию вредных веществ в воздухе и фиксировать количество легочных заболеваний населения в месяц. Можно через равные промежутки времени сопоставлять доходность акций данной корпорации с каким-либо индексом, характеризующим среднюю доходность всего рынка акций. В этом случае генеральная совокупность представляет собой двумерную случайную величину , . Эта случайная величина принимает значения x, y на множестве объектов генеральной совокупности. Не зная закона совместного распределения случайных величин  и , мы не можем говорить о наличии или глубине корреляционной связи между ними, однако некоторые выводы можно сделать, используя выборочный метод.

Выборку объема n в этом случае представим в виде таблицы, где i-тый отобранный объект (i= 1,2,...n) представлен парой чисел x_i, y_i :

x1	x2	...	xn
y1	y2	...	yn

Выборочный коэффициент корреляции рассчитывается по формуле

Здесь

,,

.

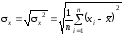Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции _, характеризующего генеральную совокупность.

51. Метод максимального правдоподобия

Ме́тод максима́льного правдоподо́бия или метод наибольшего правдоподобия (ММП, ML, MLE — англ.maximum likelihood estimation) в математической статистике— это метод оценивания неизвестного параметра путём максимизациифункции правдоподобия^[1]. Основан на предположении о том, что вся информация остатистической выборкесодержится в функции правдоподобия

Пусть есть выборкаизраспределения, где— неизвестные параметры. Пусть—функция правдоподобия, где.Точечная оценка

называется оце́нкой максима́льного правдоподо́бия параметра . Таким образом оценка максимального правдоподобия — это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.

Часто вместо функции правдоподобия используютлогарифмическую функцию правдоподобия. Так какфункциямонотонно возрастаетна всей области определения,максимумлюбой функцииявляется максимумом функции, и наоборот. Таким образом,

,

Если функция правдоподобия дифференцируема, то необходимое условие экстремума — равенство нулю ее градиента:

• Оценки максимального правдоподобия, вообще говоря, могут быть смещёнными(см. примеры), но являютсясостоятельными,асимптотически эффективными и асимптотически нормальными оценками. Асимптотическая нормальность означает, что

где - асимптотическая информационная матрица

Асимптотическая эффективность означает, что асимптотическая ковариационная матрица является нижней границей для всех состоятельных асимптотически нормальных оценок.

• Если 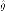— оценка метода максимального правдоподобия, параметров, тоявляется оценкой максимального правдоподобия для, где g-непрерывная функция (функциональная инвариантность). Таким образом, законы распределения данных можно параметризовать различным образом.

у́нкция правдоподо́бия в математической статистике— этосовместное распределениевыборкииз параметрического распределения, рассматриваемое как функция параметра. При этом используется совместная функция плотности (в случае выборки из непрерывного распределения) либо совместная вероятность (в случае выборки из дискретного распределения), вычисленные для данных выборочных значений. Если распределение вероятности зависит от параметра, то с одной стороны можно рассматривать вероятность некоторых событий при заданном параметре, а с другой стороны — вероятность заданного события при различных значениях параметра. То есть в первом случае имеем функцию, зависящую от события, а во втором — от параметра при фиксированном событии. Последний вариант является функцией правдоподобия и показывает, насколько правдоподобен выбранный параметр при заданном событии. Неформально: если вероятность позволяет нам предсказывать неизвестные результаты, основанные на известных параметрах, то правдоподобие позволяет нам оценивать неизвестные параметры, основанные на известных результатах.

,

52. Интервальное оценивание. Основные понятия

53