Ответы

Ускорение электронов осуществляется высоким напряжением U, создаваемым между катодом и антикатодом.

Под действием напряжения U электроны разгоняются до энергии eU. Попав в металлический антикатод, электроны резко тормозятся, вследствие чего и возникает так называемое тормозное рентгеновское излучение. Спектр этого излучения при разложении по длинам волн оказывается сплошным, как и спектр видимого белого света. На рис. 39 показаны экспериментальные кривые распределения интенсивности

(т.е.⁄ ) по длинам волн , полученные для разных значений ускоряющего на-

пряжения U на электродах трубки.

При торможении бомбардирующих анод рентгеновской трубки электронов, энергия которых не превышает определенной характерной для вещества анода величины,

возникает сплошной рентгеновский спектр, не зависящий от материала анода, а определяемый только энергией бомбардирующих анод электронов и называемый тормозным спектром.

Отметим, что существование сплошного рентгеновского спектра не противоречит классической теории излучения, так как при торможении движущихся зарядов должно действительно возникать излучение со сплошным спектром.

Экспериментальное исследование тормозного спектра показало:

1)существование максимума интенсивности, смещающегося с повышением напряжения в сторону коротких волн;

2)существование минимальной длины волны – границы сплошного спек-

тра,– не зависящей от вещества анода, а определяемой только кинетической энер-

гией электронов, вызывающих тормозное рентгеновское излучение (чем больше

энергия, тем меньше ).

Существование коротковолновой границы сплошного спектра не согласуется с выводами классичесской электродинамики, но вытекает из квантовых представле-

ний: энергия рентгеновских фотонов h , возникающих при торможении электронов,

не может превышать кинетическую энергию eU этих электронов, т.е.

≤

Возбуждение характеристических рентгеновских спектров обязано процессам,

происходящим во внутренних, застроенных оболочках атомов, имеющих сходное строение. Схема их возникновения представлена на рис. 43. Пусть под влиянием

внешнего электрона или высокоэнергетического фотона вырывается один из внутренних K-электронов металла анода. Тогда на его место может перейти электрон с более удаленных от ядра оболочек L, М, N, ... Такие переходы сопровождаются испусканием рентгеновских квантов и возникновением спектральных линий K-серии:

(L → K), (М → K), (N → K) и т.д. Самой длинноволновой линией K-серии

является линия K . Частоты линий возрастают в ряду → → , поскольку энер-

гия, высвобождаемая при переходе электрона на K-оболочку с более удаленных обо-

лочек, увеличивается. Наоборот, интенсивности линий в ряду → → убыва-

ют, так как вероятность переходов электронов с L-оболочки на K-оболочку больше,

чем с более удаленных оболочек М и N.

K-серия сопровождается обязательно другими сериями, так как при испускании ее линий появляются вакансии в оболочках L, М, ..., которые будут заполняться электронами, находящимися на более высоких уровнях. Возникновение дальнейших серий L, М, ... объясняется аналогичным образом; впрочем, они наблюдаются только для тяжелых элементов. Отметим, что линии характеристического рентгеновского излучения могут иметь тонкую структуру, т.е. энергетические уровни (а они, как известно, определяются главным квантовым числом) расщепляляются согласно значениям орбитального и магнитного квантовых чисел.

Рентгеновские спектры поглощения отличаются от рентгеновских спектров излучения: они состоят из нескольких полос с резким длинноволновым краем (рис. 45).

В результате поглощения рентгеновского фотона атомом может произойти вырывание электрона с одной из внутренних оболочек атома (процесс фотоионизации), причем каждая из полос поглощения соответствует вырыванию электрона из определенной оболочки атома (K-полоса соответствует выбиванию электрона из самой внутренней оболочки и т.д.). Резкий длинноволновый край полос соответствует началу процесса фотоионизации. Из рис. 45 также следует, что полосы поглощения обладают тонкой структурой: в K-полосе – один максимум, в L-полосе – 3 максимума, в M-полосе – 5 максимумов. Отметим, что структура рентгеновских спектров поглощения тяжелых атомов аналогична, что говорит об идентичности строения внутренних оболочек атомов тяжелых элементов.

33.Основные постулаты квантовой механики. Чистые и смешанные состояния квантово-механической системы. Волновая функция, матрица

плотности.

Постулаты:

Каждой физической величине сопоставляется линейный эрмитов оператор . .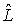

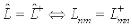Каждому чистому состоянию физической системы сопоставляется нормированная волновая функция .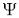

Физическая величина L может принимать только значения, равные собственным значениям оператора .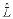

Математическое ожидание 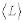величины 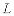в состоянии 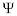определяется диагональным матричным элементом .

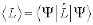Матричные элементы операторов декартовых координат 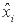и декартовых компонент обобщенного импульса 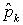, вычисленные между волновыми функциям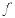и и 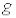системы, удовлетворяют уравнениям Гамильтона классической механики:

– оператор, соответствующий классической функции Гамильтона.

Операторы		и	удовлетворяют коммутационным соотношениям:
Замечания:
1.	Если есть физическая величина			, то в ней заменяем			. Если присутствуют члены типа	, то строим выражение
таким образом, чтобы соблюдать эрмитовость. Пример:							.
2.	Если	не является собственной функцией		, то	, где	.	.

,

–вероятность принять значение .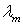

3.Под производной оператора подразумевается

Чистые и смешанные состояния. Матрица плотности.

Волновая функция описывает только чистые состояния, когда состояние системы можно представить в виде линейной суперпозиции некоторых базисных состояний. Свойства матрицы плотности:

1.Всякое состояние (чистое или смешанное) описывается матрицей плотности 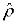, эта матрица эрмитова: .

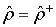2.Все собственные значения 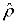лежат в интервале .

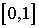.	– вероятность чистого состояния	.
3. Условие нормировки:	.

4.Если 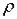– матрица плотности, то вероятность находиться в состоянии 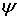равна .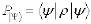

5.Среднее значение физической величины 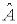в состоянии с м.п. : .

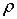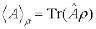6.Необходимое и достаточное условие чистоты: 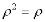. При этом 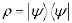, 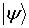– чистое состояние.

Общий вид матрицы плотности в состоянии со спином, направленным вдоль :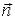

,

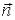характеризует направление спина, 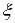– чистоту состояния ( 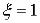– чистое). Принцип неопределенности.

Пусть 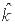и 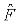– самосопряженные операторы. , где 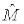– также самосопряженный оператор.

Средние значения 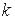и 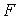по состоянию : 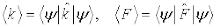Введем операторы отклонения от средних значений:

Для них выполняется коммутационное соотношение: Рассмотрим вспомогательный интеграл:

Для средних значений:	.
Если положить	, получим соотношение неопределенностей Гейзенберга:

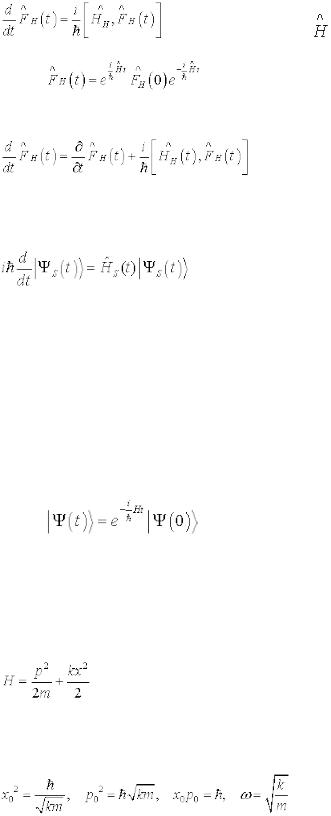
35.Описание эволюции квантово-механических систем. Уравнения Гейзенберга и Шредингера. Стационарные состояния.

Эволюцию квантовомеханической системы можно рассматривать двумя способами:

1) Операторы физических величин зависят от времени, а ВФ – нет. (представление Гейзенберга) Тогда для оператора 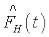физической величины выполняется уравнение Гейзенберга:

	– для консервативных систем (	не зависит от времени).
Решение:	.
Общий вид ур-я Гейзенберга:

2) ВФ состояний зависят от времени, а операторы физических величин – нет. (представление Шредингера)

Общий вид уравнения Шредингера:

Состояния, описываемые собственными функциями гамильтониана 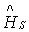, называются стационарными, а множество собственных значений – энергетическим спектром.

Эволюция матрицы плотности:

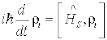, где - матрица плотности

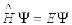– стационарное уравнение Шредингера.

Решение: .

Представление Гейзенберга и представление Шредингера эквивалентны:

,

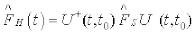
Линейный квантовый гармонический осциллятор. Энергии и волновые функции стационарных состояний.

Введем операторы: .

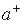– оператор рождения, 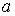– оператор уничтожения. Если выразить эти операторы через и 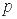и воспользоваться коммутационными соотношениями

для 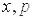, то можно показать, что .

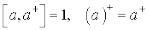Гамильтониан, выраженный через новые операторы:

.

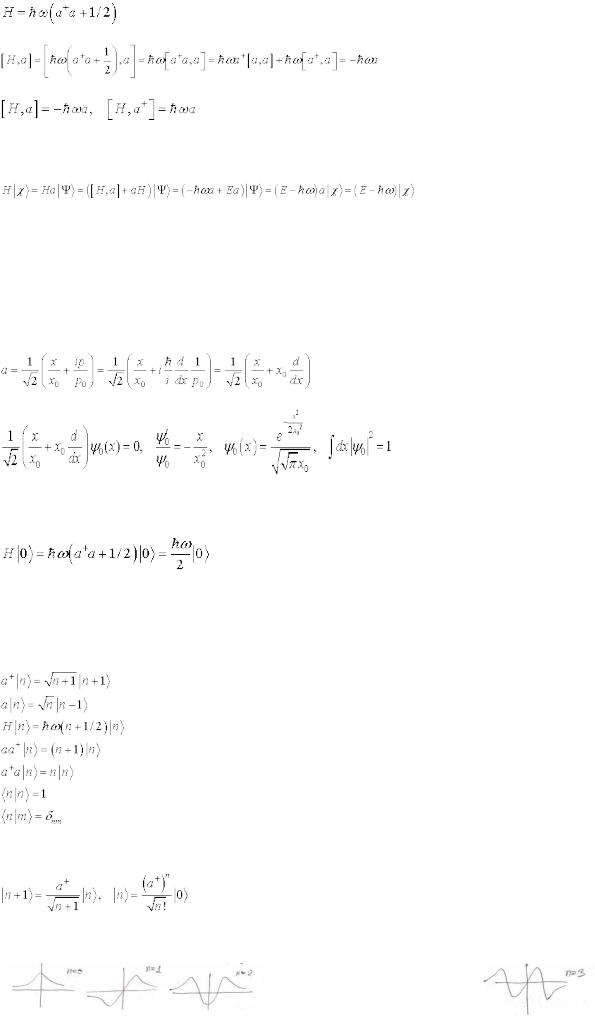
Пусть мы нашли решение 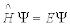. Рассмотрим состояние :

.

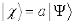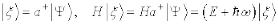Таким образом, оператор 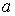уменьшает энергию на , 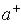– увеличивает на , и эти операторы строят ненормированные ВФ новых состояний. Найдем один уровень:

введем основное состояние – вакуум. .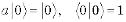

В координатном представлении .

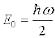– энергия основного состояния.

Можно доказать следующие равенства:

Все ВФ строятся следующим образом:

Количество нулей ВФ совпадает с .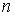

Прохождение частиц через потенциальный барьер. Туннельный эффект.

Гамильтониан свободной частицы в 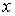-представлении:

Уравнение Шредингера: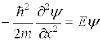

Решение:

Потенциальный барьер:

:

:

:

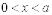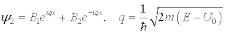
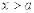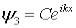
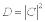– коэффициент прохождения. 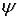и 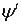непрерывны.

При : .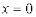

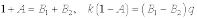При : .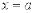

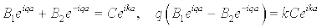Если 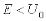, то 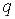– чисто мнимое.

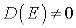при конечных .

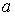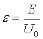
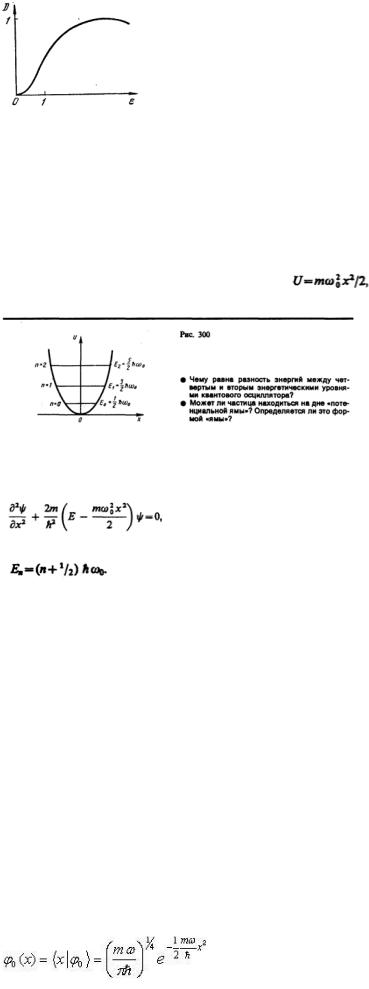
1. В действительности для разной ширины барьера получается разная кривизна графика в области E<U0. Именно, для малых ширин вторая производная отрицательна, для больших - положительна. 2. При больших E коэффициент прохождения стремится к 1. Другое дело, что это стремление сопровождается осцилляциями убывающей амплитуды. Осцилляции связаны с интерференцией (два скачка потенциала), именно из-за нее в формуле стоит sin qa.

36.Линейный квантовый гармонический осциллятор. Энергии и волновые функции стационарных состояний.

Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна

(222.1)

где w0 — собственная частота колебаний осциллятора, т — масса частицы. Зависимость (222.1) имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.

Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е (см. рис. 16). В точках с координатами ±xmax полная энергия Еравна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (–xmax, +xmax). Такой выход означал бы, что ее потенциальная энергия больше полной, что абсурдно, так как приводит к выводу, что кинетическая энергия отрицательна. Таким образом, классический осциллятор находится в «потенциальной яме» с координатами – xmax <х< xmax «без права выхода» из нее.

Гармонический осциллятор в квантовой механике — квантовый осциллятор — описывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

(222.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что уравнение (222.2) решается только при собственных значениях энергии

(222.3)

Формула (222.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным значением энергии E0=1/2ћw0. Существование минимальной энергии — она называется энергией нулевых колебаний — является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей. Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоречит выводам классической теории, согласно которой наименьшая энергия, которую может иметь осциллятор, равна нулю (соответствует покоящейся в положении равновесия частице). Например, классическая физика приводит к выводу, что при Т=0 энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное колебаниями атомов. Однако эксперимент показывает, что интенсивность рассеяния света при понижении температуры не равна нулю, а стремится к некоторому предельному значению, указывающему на то, что при Т®0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний.

Из формулы (222.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга, а именно расстояние между соседними энергетическими уровнями равно ћw0, причем минимальное значение энергии E0=1/2ћw0.

Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области |x|£xmax , в то время как с классической точки зрения она не может выйти за пределы области (–xmax, +xmax). Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без его вывода) демонстрируется на рис. 301, где приводится квантовая плотность вероятности w обнаружения осциллятора для состояния п=1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности w имеет конечные значения за пределами классически дозволенной области |x|£xmax, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу в области за пределами «потенциальной ямы». Существование отличных от нуля значений w за пределами «потенциальной ямы» объясняется возможностью прохождения микрочастиц сквозь потенциальный барьер.

Волновые функции стационарных состояний

Перейдем в представление { 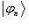} и запишем функции 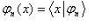, представляющие собственные состояния гамильтониана.

Мы уже определили функцию 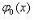, представляющую основное состояние :

. (77)

Фигурирующая перед экспонентой константа обеспечивает нормировку функции .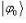

Чтобы получить функции 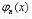, связанные с другими стационарными состояниями гармонического осциллятора, достаточно использовать выражение (67) для кет-

вектора

и тот факт, что в представлении {

} операторa+ представлен выражением

, поскольку Х представлен умножением

на х, а Р - дифференцированием (формула (16)). Тогда:

(78)

или

. (79)

Нетрудно видеть из этого выражения, что 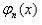является произведением экспоненты 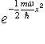на полином степени n и четности (-1)n, который называется полиномом Эрмита.

Несложные вычисления дают первые функции :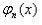

;

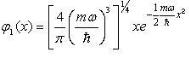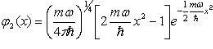. (80)

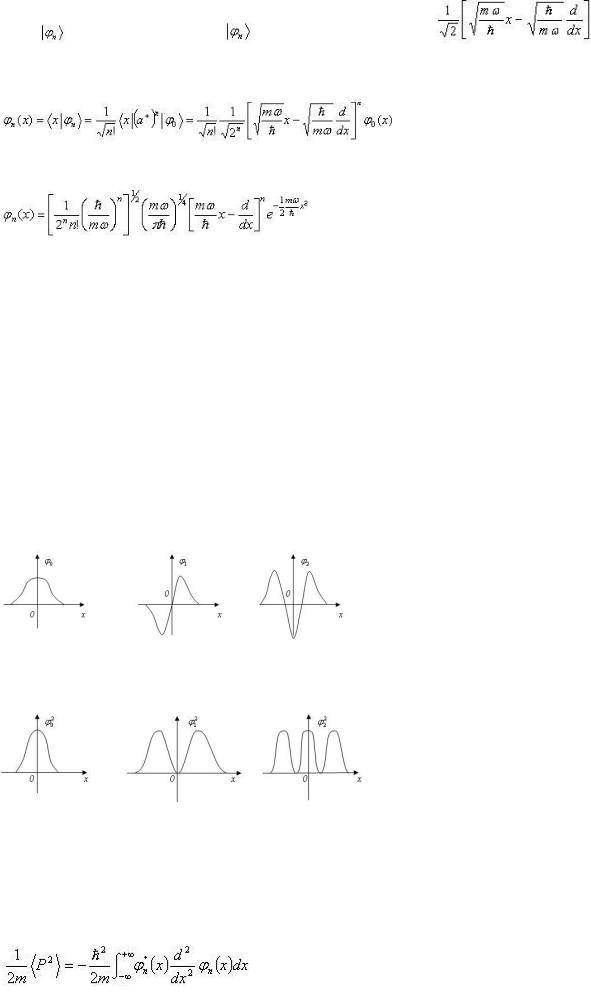
Эти функции представлены на рис. 3, а соответствующие им плотности вероятности приведены на рис. 4.

Рис. 3.

Волновые функции трех первых уровней гармонического осциллятора

Рис. 4.

Плотность вероятности трех первых уровней гармонического осциллятора

Амплитуда колебаний частицы увеличивается с ростом ее энергии. Среднее значение потенциальной энергии также увеличивается с ростом n, так как при больших

значениях n функция 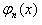заметно отлична от нуля в тех областях оси Ох, где потенциал V(x) увеличивается. Кроме того, число нулей функции равно n, и средняя кинетическая энергия частицы увеличивается с ростом n. Действительно, она определяется формулой:

. (81)

С увеличением количества нулей функции 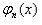кривизна волновой функции возрастает, и в формуле (81) вторая производная 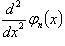принимает все большие и большие значения.

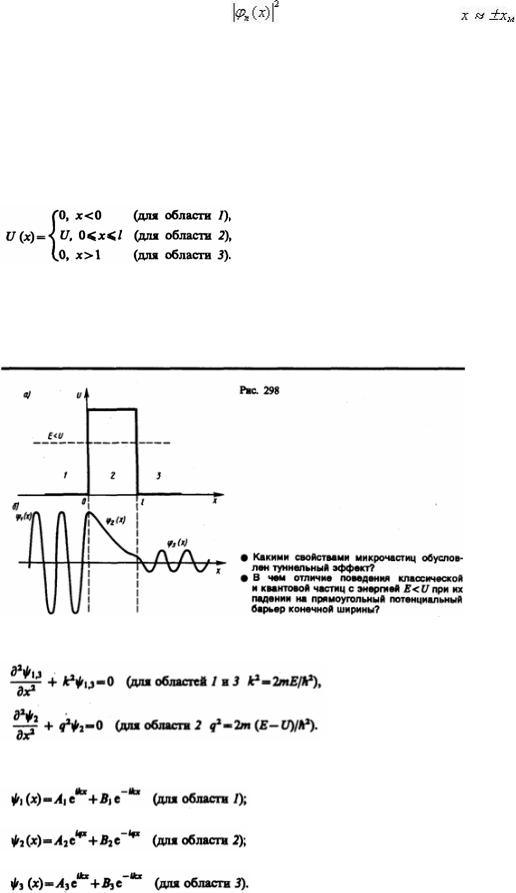
Наконец, при больших n плотность вероятности

принимает наибольшие значения при

. Этот результат напоминает характеристику движения,

которую предсказывает классическая механика: классическая частица имеет нулевую скорость в точках 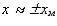; т.е. она в среднем проводит больше времени вблизи этих точек, чем в центре интервала .

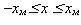37. Прохождение частиц через потенциальный барьер. Туннельный эффект.

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины l можем записать

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>1, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.

Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид

(221.1)

Общие решения этих дифференциальных уравнений:

(221.2)

(221.3)

В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид

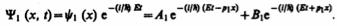(221.4)

В этом выражении первый член представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй — волну, распространяющуюся в противоположном направлении, т. е. отраженную от барьера (соответствует частице, движущейся от барьера налево).

Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент B3 в формуле (221.3) следует принять равным нулю.