Операции над множествами

Основными операциями над множествами являются: объединение – , пересечение - , вычитание (разность) - \ , сумма -  и унарная операция дополнение - .

Операция объединения -  . Объединением двух множеств А и В называется такое множество С, элементы которого состоят из элементов множества А и из элементов множества В.

А  В = {x | x  А и/или х  В}.

Пусть С = А  В, тогда, если х  С, то х  А и/или х  В.

Пример:

Пусть заданы множества A = {0, 1, 2, 3, 4} и B = {3, 4, 5, 6}. Тогда А  В = C = {0, 1, 2, 3, 4, 5, 6}.

Операция пересечения -  . Множество С есть пересечение множеств А и В, если каждый элемент множества С является элементом А и В одновременно.

С = А  В = { x | x  А и х  В}.

Союз «и» заменяют часто знаком &.

Если x  С, то x  А & х  В ;

Пример:

Если A = {0, 1, 2, 3, 4}, B = {3, 4, 5, 6}, то C = {3, 4}.

Операция разность - \ . Разностью множеств А и В называется множество С, элементы которого принадлежат А, но не принадлежат В.

С = А \ В = { x | x  А и х  В}.

Если x  С, то x  А и х  В.

Для предыдущего примера С = А \ В = {0, 1, 2}; C’ = B\ A = {5, 6}.

Операция сумма -  (симметрическая разность) .

С = А  В = (А \ В)  (В \ А)

Если x  С, то х является элементом разности А и В или элементом разности В и А.

С = А  В = {x | x  А / В или x  В \ А}

То есть, если А={1,2,3,4,5}, В={3,4,5,6,7}, тогда С = А  В={1,2,6,7}.

Операция дополнение (одноместная операция). Дополнение А обозначается ¬А, Ā, А', содержит все те элементы универсального множества I, которые не принадлежат А.

С = Ā = I \ А

Пусть I = {0,1,2,3,4,5,6,7,8,9}. A={3,8,5,7,0}. Тогда Ā={1, 2, 4, 6, 9}.

Диаграммы Эйлера – Венна

Возможно графическое представление множеств. Универсальное множество задается в виде квадрата, а множества А и В как множества точек плоскости, ограниченные соответствующими замкнутыми линиями. Например: на рисунке 1.1 изображены непересекающиеся (а) и пересекающиеся (б) множества А и В. На рисунке 1.2. показано отношение включения А  В.

Следующие рисунки демонстрируют результаты выполнения операций над множествами (показаны заштрихованной областью). Диаграммы приведенные на рисунке 1.3, демонстрируют объединение множеств А и В.

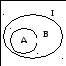
а б

Рисунок 1.1 - Пример множеств Рисунок 1.2 А  В

Рисунок 1.3 – Объединение множеств А В

На рисунке 1.4 приведены примеры пересечения. На рисунке 1.4 а приведены множества имеющие одинаковые элементы, их пересечение А ∩ В  , и случай 1.4 б множества не имеют общих элементов, и их пересечение А ∩ В = .

а б

Рисунок 1.4. Пересечение А ∩ В

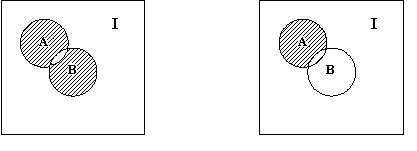
Рисунок 1.5 - Cумма А  В Рисунок 1.6 - Разность А \ В

Рисунок 1.7 - Дополнение Ā

Понятие алгебры

Алгеброй А называется совокупность множества М с заданными в нем операциями:

S = {f₁, f₂, …, f_m1, f_m2, …, f_m,_nm },

A = < M, S >, здесь множество М – носитель, S – сигнатура алгебры. Нижний индекс у идентификатора операции указывает ее местность.

Алгебра вида < M, f₂ > называется группоидом.

Если f₂ – операция типа умножения, то группоид называется мультипликативным, если f₂ – операция типа сложения, то аддитивным.

Пусть А = <M, f₂> - группоид. Обозначим операцию f₂ как . Тогда элемент ℓ, ℓ М, называется правым нейтральным элементом, если m М, и m  ℓ = m. Если ℓ  m = m – левым нейтральным элементом. Если выполнены оба соотношения, ℓ называется двусторонним нейтральным элементом, или просто нейтральным элементом.

Если группоид <М, •> мультипликативный, то нейтральный элемент называется единицей и обозначается 1.

Если группоид <М, •> - аддитивный, то нейтральный элемент называется нулем и обозначается 0.

Группоид А = <М, •> называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности:

m  M, m • m = m.

Группоид А = <М,•>, сигнатура которого удовлетворяет закону коммутативности:

х,у  М, х•у = у•х,

называется коммутативным или абелевым.

Группоид <М,•>, в котором выполняется закон ассоциативности:

х,у,z  М х•(у•z) = (x•у)•z,

называется ассоциативным или полугруппой.

Полугруппа <М,•>, в которой выполнимы обратные операции, т.е. для любых а, b  М каждое из уравнений а•х = b, у•а = b обладает единственным решением, называется группой.

Алгебра <М, *, +>, которая по умножению является мультипликативным группоидом, а по сложению – абелевой группой, причем умножение связано со сложением законами дистрибутивности

а * (b+c) = a * b + a * c, (b+c) * a = b * a + c * a

называется кольцом. Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом. Тело, у которого мультипликативная группа абелева, называется полем.

Рассмотрим алгебру множеств

А_к = < B(1),  , , ‾ >

Носителем является булеан универсального множества 1, сигнатурой – операции , , ‾ . Для операций алгебры множеств выполняются законы:

1. Коммутативности объединения и пересечения:

АВ = ВА; АВ = В  А.

2. Закон ассоциативности:

А (ВС) = (АВ)  С;

А (ВС) = (АВ) С.

3. Закон дистрибутивности пересечения относительно объединения и объединения относительно пересечения:

А  (ВС) = А ВАС;

А (ВС) = (АВ)  (АС).

4. Законы поглощения:

ААВ = А; А  (АВ) = А.

5. Законы склеивания:

А ВА  = А; (АВ)  (А  ) = А.

6. Законы Порецкого:

АĀВ = АВ; А  (Ā  В) = А В.

7. Закон идемпотентности:

А  А = А; А  А = А.

8. Закон действия с универсальным и пустым множествами:

М  = М, М   =  , М 1 = 1,

М 1 = М, М  =1, М  =;

9. Законы де Моргана

10. Закон двойного дополнения:

Алгебра множеств является абелевой полугруппой, но не является группой.

Докажем дистрибутивность А  (В ∩ С) = (А  В) ∩ (А  С). Доказательство проходит в два этапа. Обозначим левую часть как Z, правую – D. Требуется доказать, что если хZ, то xD и наоборот, если xD, то xZ.

1. Пусть х А  (В ∩ С) , это значит, что хА или х(В∩С).

Пусть хА, тогда хА  В и хА  С, из чего следует х(А В) ∩ (А С).

Если х(В∩С), тогда хВ и хС; из чего следует хА В и хА С то есть х(А В) ∩ (А С).

Первая часть утверждения доказана.

2. Если х(А В) ∩ (А С), тогда хА В и хА С,

Если хА, то хА (В∩С);

Если х  А, то х В и х С, тогда х В ∩ С, из чего следует

х А  (В ∩ С).