- •5. Выполним оптимизацию сетевого трафика по времени.
- •2. Так как прямая задача является задачей максимизации, двойственная задача будет задачей минимизации.
- •Определим изменение максимальной прибыли от реализации продукции при увеличении запаса ресурса 1 на 10 ед., ресурса 2 – на 50 ед. И уменьшении запаса ресурса 3 на 30 ед.
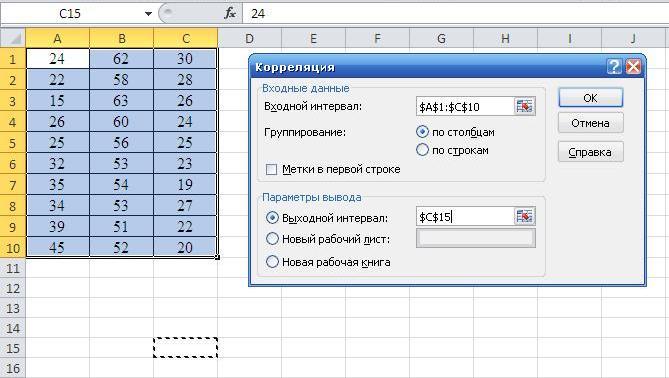
- •Определение коэффициента корреляции между показателями
- •Итоги расчетов по модели линейной регрессии
2. Так как прямая задача является задачей максимизации, двойственная задача будет задачей минимизации.
Система ограничений прямой задачи состоит из трёх ограничений. Следовательно, в двойственной задаче будут три переменные y1, y2, y3.
Систему ограничений прямой задачи надо вначале привести к стандартному виду, то есть в задаче на максимум все ограничения должны быть вида ≤ или =. Тогда в двойственной задаче на минимум все ограничения будут вида ≥ или =.
Составляем систему ограничений двойственной задачи.
Матрица коэффициентов при неизвестных в неравенствах двойственной задачи получается транспонированием матрицы коэффициентов прямой задачи, неравенства меняются на противоположные, а свободные члены совпадают с коэффициентами целевой функции прямо задачи.
min F = 30у1 + 500у2 + 140у3
у1 + 6у2 + 4у3 ≥ 60
у1 + 5у2 + 6у3 ≥ 70
у1 + 4у2 +10 у3 ≥ 120
у1 + 3у2 + 13у3 ≥ 130
у1, у2, у3 ≥ 0
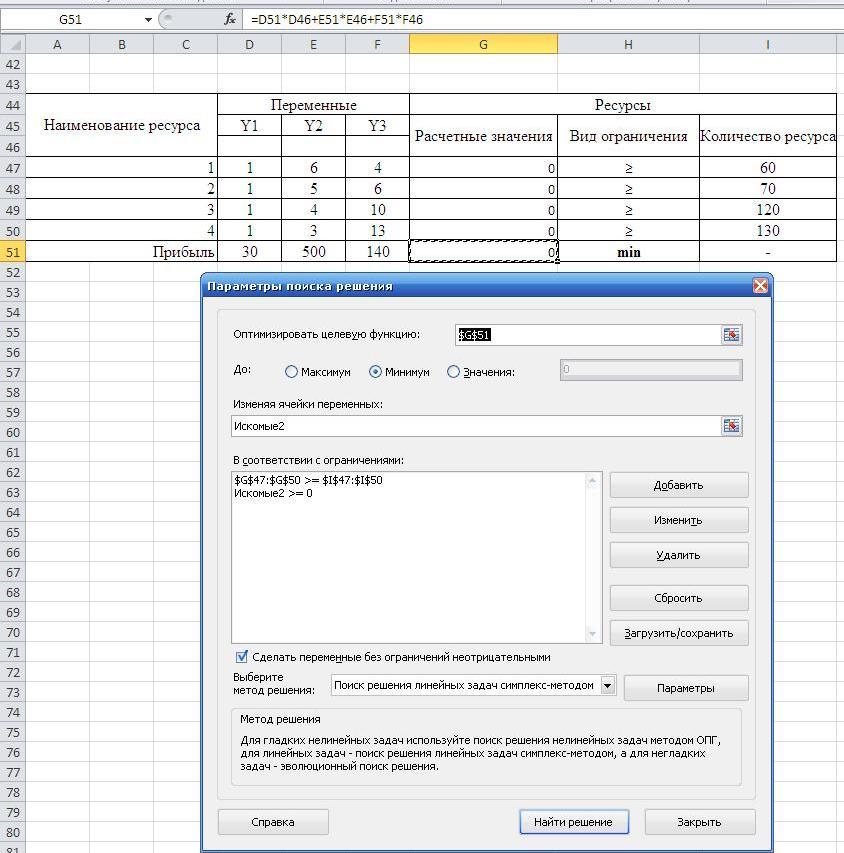
Для этого внесем исходные данные в таблицу, осуществим абсолютную адресацию к блоку переменных (у1, у2, у3), которому дадим уникальное имя «Искомые2».
Поиск решения двойственной задачи.
Результаты решения двойственной задачи.
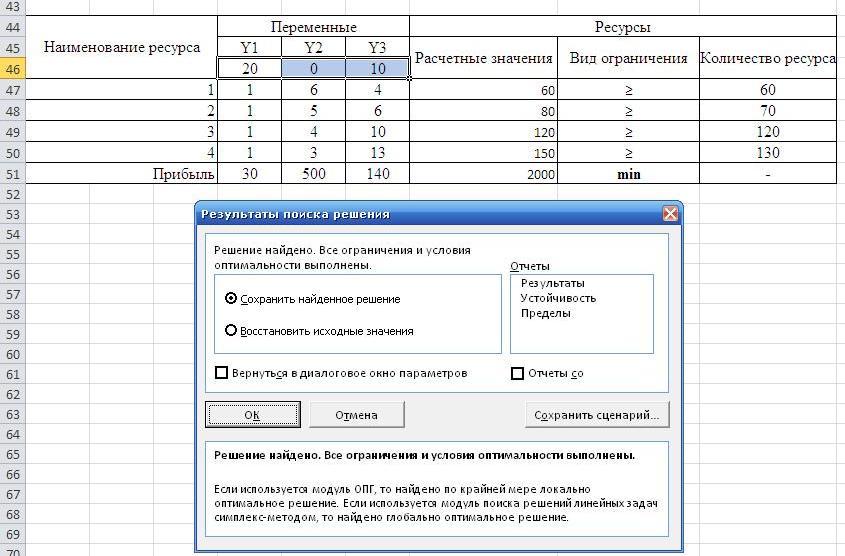
Оптимальный план
минимизации задачи
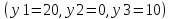 единиц. Проведем анализ полученного
оптимального решения исходной задачи
с помощью двойственных оценок.
единиц. Проведем анализ полученного
оптимального решения исходной задачи
с помощью двойственных оценок.
Объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т.е. полностью используемые) ресурсы получают ненулевые оценки, а недефицитные — нулевые оценки.
Ресурсы 1 и 3 имеют отличные от нуля оценки 3,33 и 26,6 – эти ресурсы полностью используются в оптимальном плане, являются дефицитными, сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям. Ресурсы 2 и 4 – являются недефицитными.
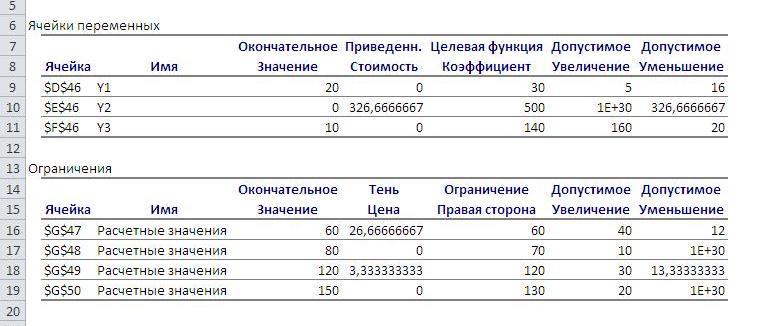
3. В разделе отчета «Ограничения» теневые цены это двойственные оценки ресурсов, а Допустимое увеличение и уменьшение показывают допустимые диапазоны изменения правых частей ограничений, в пределах которых в оптимальный план входят те же переменные, хотя возможно и с другими значениями.
Интервалы устойчивости двойственных оценок по отношению к изменению запаса ресурсов каждого вида будут следующие:
Ресурс 1: допустимое увеличение на 40 единиц и допустимое уменьшение – 12 единиц.
Ресурс 2: допустимое увеличение на 10 единиц и допустимое уменьшение – бесконечность.
Ресурс 3: допустимое увеличение на 30 единиц и допустимое уменьшение – 13 единиц.
Ресурс 4: допустимое увеличение на 20 единиц и допустимое уменьшение - бесконечность.
Любое увеличение или уменьшение ресурсов, при которых значение не будет попадать в соответствующий диапазон приведет к изменению структуры решения.
-
Определим изменение максимальной прибыли от реализации продукции при увеличении запаса ресурса 1 на 10 ед., ресурса 2 – на 50 ед. И уменьшении запаса ресурса 3 на 30 ед.
Тогда исходная таблица примет вид:
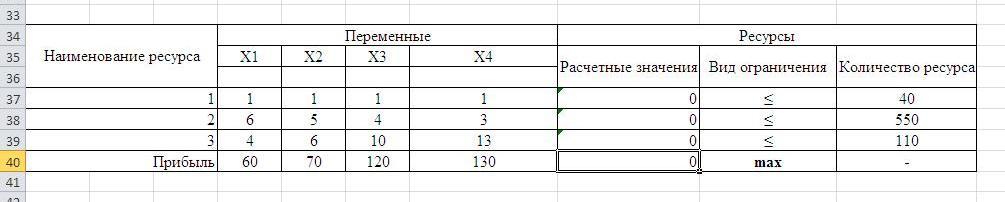
Результаты решения после изменений всех запасов ресурсов.

Изменение всех запасов влияет на прибыль (максимальная прибыль становится меньше исходной), в то же время количество необходимых ресурсов так же уменьшается.
Увеличение ресурса 1 на 10 единиц приводит к еще большей максимизации прибыли, при этом количество ресурсов 1 и 2 требуется больше.
Результаты решения после изменения количества ресурса 1.
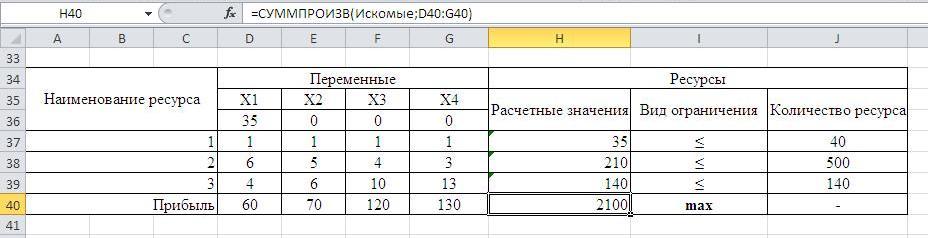
Увеличение ресурса 2 на 50 единиц не влияет ни на прибыль, ни на коэффициенты X, ни на требуемое количество ресурсов.
Результаты решения после изменения количества ресурса 2.
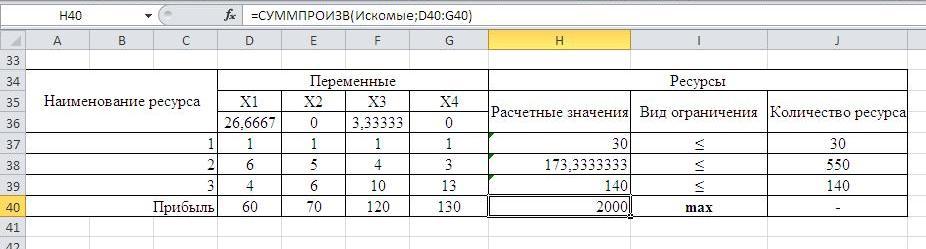
Уменьшение ресурса 3 на 30 единиц приводит к уменьшению максимальной прибыли.
Результаты решения после изменения количества ресурса 3.
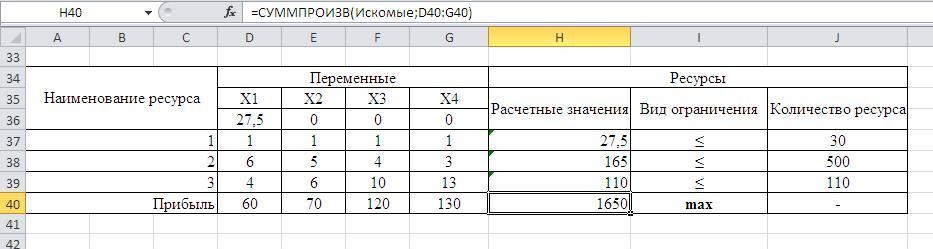
Вывод. Таким образом, самый выгодный путь для еще большей максимизации прибыли – увеличение ресурса 1 на 10 единиц.
№4. Транспортная задача или Модели управления запасами.
Решить транспортную задачу - исходные данные транспортной задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху – мощности потребителей. Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя «Поиск решения».
|
Вариант 10 |
|||||
|
|
7 |
7 |
7 |
7 |
2 |
|
4 |
16 |
30 |
17 |
10 |
16 |
|
6 |
20 |
27 |
26 |
9 |
23 |
|
10 |
13 |
4 |
22 |
3 |
1 |
|
10 |
3 |
1 |
5 |
4 |
24 |
Решение.
Экономическая постановка задачи следующая:
В 4 пунктах
отправления A13,
A14,
A15,
A16
сосредоточен однородный груз в количествах
соответственно 4, 6, 10, 10 единиц. Имеющийся
груз необходимо доставить потребителям
B12,
С12, D12,
E12,
F12,
спрос которых выражается величинами
7, 7, 7, 7, 2 единиц соответственно. Известна
стоимость
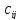 перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения. Требуется составить
план перевозок, который полностью
удовлетворит потребителей в грузе и
при этом суммарные транспортные издержки
минимизируются.
перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения. Требуется составить
план перевозок, который полностью
удовлетворит потребителей в грузе и
при этом суммарные транспортные издержки
минимизируются.
Математическая постановка этой задачи имеет вид:
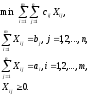
Здесь
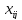 – объем,
– объем,
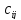 – тариф поставки
продукции от i-го
поставщика к j-му
потребителю,
– тариф поставки
продукции от i-го
поставщика к j-му
потребителю,
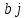 – потребности
потребителей в продукции,
– потребности
потребителей в продукции,
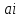 - запасы продукции у поставщиков.
- запасы продукции у поставщиков.
Запишем в системе Excel исходные данные в две таблицы и сформируем вычисляемую ячейку значения целевой функции. В изменяемую таблицу Объемы перевозок первоначально для контроля введем единицы.. В целевую ячейку запишем функцию =СУММПРОИЗВ(B13:F16;B3:F6), которая вычисляет совокупные затраты на перевозку грузов от поставщиков к потребителям. В ячейках Итого поместим формулы сумм объемов перевозок по строкам и столбцам.
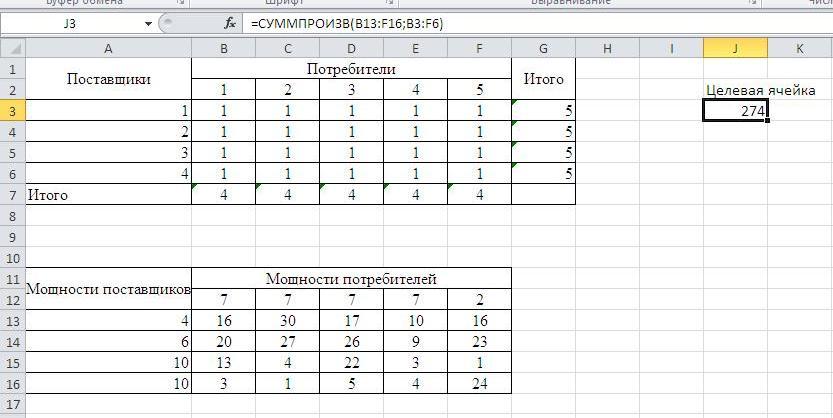
Затем вызываем функцию Поиск решения и осуществляем ввод данных в окно функции, переключатель установим в положение минимального значения. После ввода данных введем ограничения по мощностям поставщиков и потребителей.
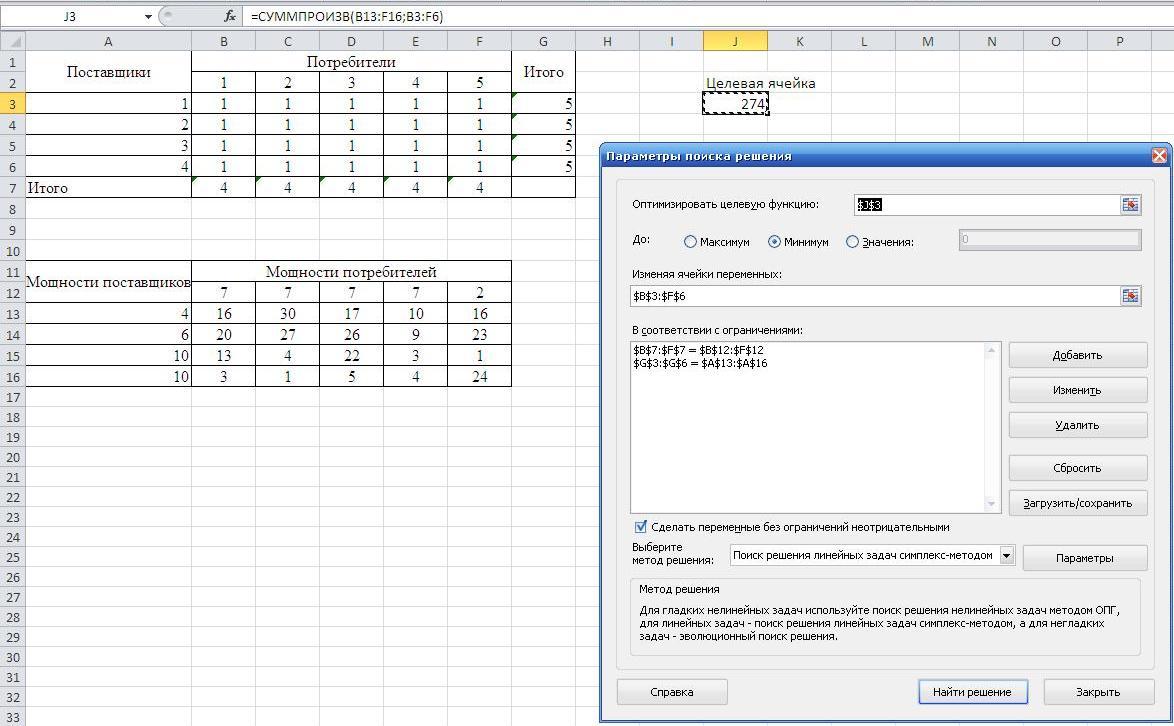
В окне Параметры поиска решения установим параметры решения задачи. После этого выполним возврат в окно «Поиск решения», где нажмем кнопку «Найти решение».
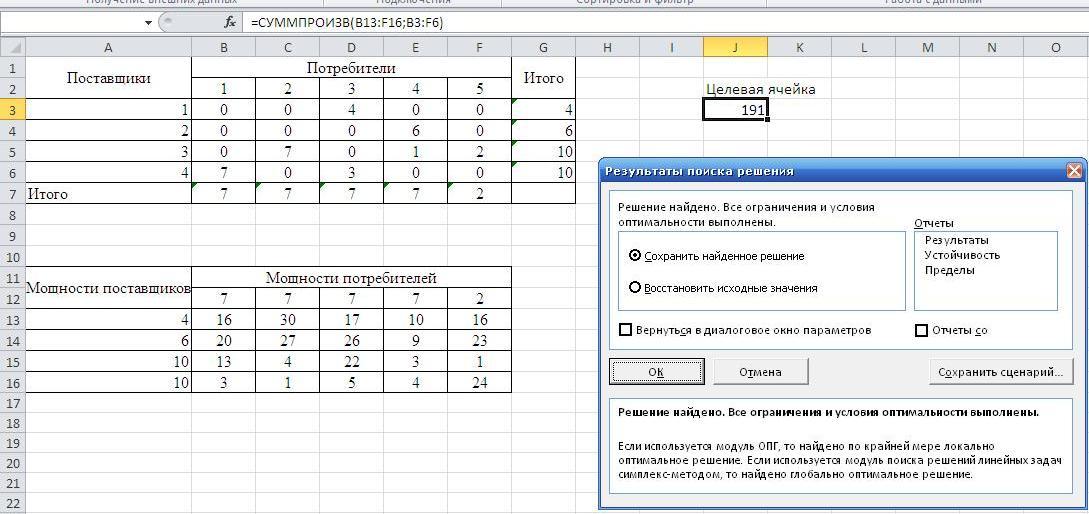
Оптимальный план перевозок с минимальными затратами равными 191 денежных единиц. Решение единственно для данной транспортной задачи.
№5. Модель множественной линейной регрессии
В таблице для каждого варианта заданы три временных ряда: первый из них представляет ВНП (млрд $) за 10 лет уt, второй и третий ряд – потребление (млрд $) х1t и инвестиции(млрд $) х2t.
-
Вычислить матрицу коэффициентов парной корреляции и проанализировать тесноту связи между показателями.
-
Построить линейную и нелинейную модели регрессии, описывающие зависимость уt от факторов х1t и х2t
-
Оценить качество моделей. Вычислить среднюю ошибку аппроксимации и коэффициент детерминации.
-
Проанализировать влияние факторов на зависимую переменную (β-коэффициент) и оценить их значимость, найти доверительный интервал.
-
Проверить остатки на нормальность распределения.
-
Определить точечные прогнозные оценки ВНП для 5 наблюдений (объясняющие переменные задать самостоятельно).
|
Вариант 10 |
|||||||||
|
24 |
22 |
15 |
26 |
25 |
32 |
35 |
34 |
39 |
45 |
|
62 |
58 |
63 |
60 |
56 |
53 |
54 |
53 |
51 |
52 |
|
30 |
28 |
26 |
24 |
25 |
23 |
19 |
27 |
22 |
20 |
Решение.
1. Вычислим матрицу коэффициентов парной корреляции и проанализируем тесноту связи между показателями с помощью MS Excel.
Для этого введем данные в таблицу MS Excel Данные и выберем функцию «Анализ данных», режим Корреляция.