Раздел 2. Информационные основы построения эвм
Тема 2.1. Системы счисления. Формы представления, виды кодирования и форматы чисел, применяемые в эвм
2.1.1. Системы счисления, применяемые в эвм
Системой счисления называется совокупность цифровых знаков и правил их записи, применяемых для однозначного изображения чисел.
Системы счисления подразделяются на непозиционные и позиционные.
Непозиционными называются такие системы, в которых применяется неограниченное количество цифр, причем значение каждой цифры не зависит от позиции ее в числе. Например, римская система. Эти системы неудобны и применяются редко.
Позиционными называются системы, в которых применяется ограниченный набор символов (цифр), причем значение каждой из них находится в строгой зависимости от ее позиции в числе.
Количество различных цифр, применяемых в данной системе, называется ее основанием. Например, в десятичной системе используется 10 цифр - {0,1,2, …, 9}.
Любое число в позиционной системе счисления можно представить в следующем виде:
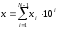(2.1)
где хi – некоторая цифра этой системы, стоящая в i-м разряде числа;
N – количество разрядов в целой части числа;
K – количество разрядов в дробной части числа (после точки);
10i – разрядный вес некоторой цифры;
10 – основание системы счисления.
Величиной основания может быть любое другое число.
В ЭВМ применяются следующие позиционные системы счисления:
двоичная – используются 2 цифры: { 0,1 };
восьмеричная – используются 8 цифр: { 0,1, 2, …, 7 };
шестнадцатеричная – используются 16 цифр: { 0,1, 2, …, 9, A, B, C, D, E, F};
десятично-двоичная – используются 10 цифр: { 0,1, 2,……9 }, но каждая цифра представлена 4-мя двоичными разрядами.
В общем случае основание системы счисления будем обозначать буквой B.
Основной системой счисления, применяемой в ЭВМ на физическом уровне, является двоичная система. Этот выбор обоснован следующими факторами:
– простота технической реализации;
– наибольшая помехоустойчивость кодирования цифр;
– минимум оборудования;
– простота арифметических действий;
– простота формального аппарата для анализа и синтеза цифровых устройств (алгебра логики).
Существуют правила перевода чисел из одной системы счисления в другую, основанные, в том числе, и на соотношении (2.1).
Например, двоичное число 1110111,011 равно десятичному числу 119,375
1110111,011(2) = 1·26+1·25+1·24+0·23+1·22+1·21+1·20+0·2-1+
+1·2-2+1·2-3 = 119,375(10)
Таким образом, для перевода числа из позиционной системы счисления в десятичную систему счисления можно использовать выражение (2.1). Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по формуле (2.1) затруднителен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в которую число переводится. Обратный перевод выполняется значительно проще, если предварительно преобразовать отдельно целую часть Xцел и дробную Xдр выражения (2.1) к виду:
Алгоритм перевода из десятичной системы счисления в систему счисления с основанием B, основанный на этих выражениях, позволяет оперировать с числами в той системе счисления, из которой число переводится, и может быть сформулирован следующим образом:
1. Для перевода целого числа в новую систему счисления его надо последовательно делить на основание новой системы счисления до тех пор, пока не получится частное, у которого целая часть равна 0. Число в новой системе записывается из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа.
2. Для перевода правильной дроби из одной позиционной системы счисления в другую дробь надо последовательно её умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представленной дроби.
Правильная дробь в новой системе счисления записывается из целых частей произведений, получающихся при последовательном умножении (причем первая целая часть будет старшей цифрой новой дроби).
Если на некотором шаге дробная часть становится равной нулю, процесс преобразования заканчивается.
При переводе в новую систему счисления неправильных дробей целую часть переводят по правилу для целых чисел, дробную – как правильные дроби. При этом все действия производят в исходной системе счисления.
Поскольку основания восьмеричной и шестнадцатеричной систем счисления (8 и 16 соответственно) является степенями числа 2, то перевод из 8-ричной системы счисления в двоичную можно произвести следующим образом: каждую цифру числа в 8-ричной системе заменить тремя двоичными разрядами. Например, число 3716(8) = (011 111 001 110)(2).
Для перевода числа из 16-ричной системы счисления в двоичную надо каждую цифру этого числа заменить ее двоичным эквивалентом (т.е. четырьмя двоичными разрядами).
Можно использовать этот метод и при обратном переводе из двоичной системы в восьмеричную или шестнадцатеричную систему счисления. Для этого надо число разделить на триады или тетрады (т.е. на группы по 3 или 4 разряда) и заменить их соответствующими цифрами в системе счисления, в которую двоичное число переводится. При этом целую часть надо делить на триады или тетрады, начиная с запятой влево, а дробную – вправо. Если целая часть двоичного числа не кратна триаде или тетраде, то последняя группа разрядов дополняется слева нулями до полной триады или тетрады. Если дробная часть двоичного числа не кратна триаде или тетраде, то последняя группа цифр дополняется справа нулями до полной триады или тетрады.