Из определения функционала следует, что его непрерывность зависит не только от аналитического выражения, но от нормированного пространства, на котором он задан. То есть один и тот же функционал может быть непрерывен на одном нормированном пространстве и прерываем на другом.

Примеры вариационных задач Задача 1. Нахождение плоской линии, соединяющей две заданные точки

и имеющей наименьшую длину. Исследуемый функционал – длина линии.

Решением данной задачи является отрезок прямой, соединяющей эти точки. Уравнение такой прямой находится однозначно по заданным точкам.

Задача 2. Нахождение плоской линии, соединяющей две заданные точки, по которой материальная точка скатывается под действием силы тяжести в кратчайшее время.

Исследуемый функционал – время движения точки.

Кривая, дающая минимум этому функционалу, называется брахистохроной. Именно эта задача была первой задачей вариационного исчисления.

§5.2. Простейшая задача вариационного исчисления

1. Постановка задачи

Дан функционал

b
J[y(x)] F(x, y(x), y'(x)) dx,		(5.4)
a	y y(x), x [a,b]
сопоставляющий каждой кривой AB		некоторое число

J [y(x)].

Функция F(x, y, y ) предполагается гладкой, т. е. ее частные производные до второго порядка включительно по всем аргументам x, y, y непрерывны в области

a x b
D : y .

y'

Среди функций y(x) C2 [a,b], где C 2 [a,b] – пространство функций, имеющих непрерывные производные до второго порядка на [a, b], удовлетво-

ряющих краевым условиям (концы кривой закреплены)
y(a) yA, y(b) yB ,	(5.5)

требуется найти функцию y*(x), на которой функционал (5.4) достигает экстремума, т. е. максимума, если J[y*(x)] J[y(x)], или минимума, если

J[y*(x)] J[y(x)], где y(x) y*(x).

Решение задачи проводится в рамках необходимых условий, сформулированных в теореме 5.1.

40

Теорема 5.1. Если функция y y(x) удовлетворяет условиям (5.5) и доставляет функционалу (5.4) экстремум, то она является решением уравнения Эйлера:

F

d

F

0.

(5.6)

y

y'

dx

В подробной записи уравнение (5.6) имеет вид

F

2F

y

2F

y 0.

y'

2

Кривые AB

y

y y

y y*(x), x [a,b],

являющиеся графиками функций –

решений уравнения Эйлера, называются экстремалями.

Уравнение Эйлера играет фундаментальную роль во всем вариационном исчислении.

Таким образом, решение простейшей задачи вариационного исчисления свелось к решению дифференциального уравнения (5.6) Эйлера при краевых условиях (5.5).

2. Частные случаи уравнения Эйлера			y . Тогда уравне-
1-й случай. Пусть функция F F(x, y) не зависит от
ние Эйлера-Лагранжа имеет вид
	F	0	(5.7)
	y
или
(x, y) 0.			(5.8)

Уравнение (5.8) определяет некоторую кривую, которая будет единственной экстремалью для данного функционала. Для произвольных краевых условий (5.5) непрерывного решения, вообще говоря, нет.

2-й случай. Пусть F F(y') не зависит ни от х, ни от у. Тогда (5.6) имеет

вид y 0.
Из общего решения					y c1x c2 находится единственное решение при
краевых условиях (5.5).						не зависит от y. Тогда уравнение (5.6)
3-й случай. Пусть F F(x,y')
	d		F					F	c .
принимает вид					0 и имеет промежуточный интеграл
								y'	1
	dx		y'
4-й случай. Пусть F F(y,y')						не зависит от x. В этом случае уравнение
(5.6) примет вид
						F(y, y )
							c1.		(5.9)
				F(y, y ) y'
						y

41

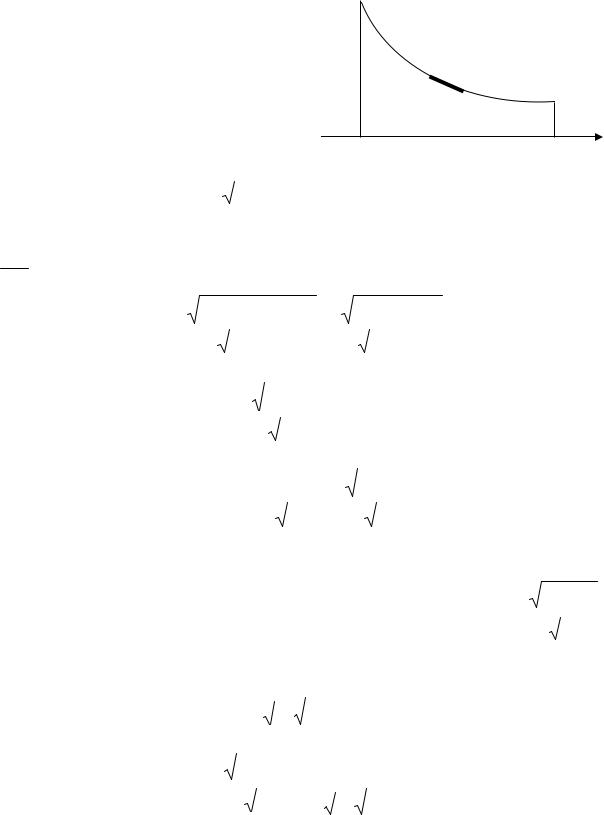
§5.3. Задача Бернулли о брахистохроне

Эта задача была поставлена в 1696 отыскании кривой «наибыстрейшего спуска» – «брахистохроне». Эта задача формулируется так: из точки A в точку B(рис. 5.1) под действием силы тяжести без начальной скорости движется точка M(x, y(x)). Какой должна быть кривая AB: y y*(x), x [a,b], чтобы время спуска по ней было минимальным?

Решение.

1. По закону сохранения энергии

		mv2
	имеем		mgy, откуда v 2gy .
		2

г. Иоганном Бернулли как задача об

A

M

ds B

a

x

b

x

Рис. 5.1

2. Тогда время пробега участка ds кривой AB находится из равенства

ds

v и, значит, dt

dt

ds

dx2 (dy(x))2

1 [y'(x)]2

dx.

v

2gy(x)

2gy(x)

3. Время спуска вдоль всей кривой

AB определится интегралом

b

1 [y'(x)]2

t

dx.

2gy(x)

a

4. Имеем функционал

T[y(x)]

1

b 1

1 y'2

dx

2g a

0

y

икраевые условия y(a) yA, y(b) yB .

5.Подынтегральная функция здесь не зависит от х, т. е. имеет место 4-й

1 y'2

случай. Применим формулу (5.9).

Согласно

(5.4), F(x, y, y )

.

y

Найдем

F

y

,

y

y

1 y'2

тогда

y 2

F y

F

1 y 2

c1.

y

y

y

1 y 2

42

6. Упростив левую часть последнего выражения, получаем

1

c1

1 y'2

или y (1 y 2) c~1.

y

7. Чтобы

решить это дифференциальное

уравнение, введем замену

y ctgt.

Тогда получим

~

~

~

c1

c

2

y

c sin

t

или

1 y 2

1 ctg2 t

c~

y

1

1 cos2t .

2

8. Найден

y как функция от t. Теперь надо отыскать x как функцию от

t. Из замены y ctgt следует, что

~

dy

~

dx

c1 sin2tdt

2c1 sintcostd t

2c~ sin2 tdt

ctgt

ctgt

cost

1

~

sint

или dx c1(1 cos2t)dt.

sin 2t

~

~

9. Интегрируя по t, получим x

c

t

c

2

или

1

2

~

x

c1

2t sin 2t c~2 .

2

10. Полагая теперь 2t , придем к функции, заданной параметрически:

c~

sin c~2,

x

2

1

~

c1

y

(1 cos ).

2

~

и

Система задает кривую,

называемую циклоидой. Обозначив x x c2

r ~c1 , получим уравнение циклоиды

2

x r sin ,

y r(1 cos ),

которое после исключения параметра принимает в декартовых координатах вид

		r y
	x rarccos			2ry y2 .
		r

43

Подставив краевые условия y(a ~c2) yA и y(b c~2) yB , получаем систему уравнений для определения констант ~c1 и c~2.

Раздел 6. Уравнения математической физики

§6.1. Понятия дифференциального уравнения в частных производных второго порядка с двумя независимыми переменными и его решения

Решение многих задач механики, физики, широкого круга инженернотехнических задач приводит к необходимости исследовать дифференциальные уравнения в частных производных второго порядка, являющихся частным случаем так называемых уравнений математической физики.

Определение 6.1. Дифференциальным уравнением в частных производ-

ных второго порядка

относительно

неизвестной

функции

u(x, y),

(x,y) D, D R2 , называется функциональная зависимость

u

u

2

u

2

u

2

u

F x, y,u,

,

,

,

,

0

(6.1)

2

2

x

y

x

x y

y

между независимыми переменными x и y,

неизвестной функцией u(x,y) и ее

частными производными до второго порядка включительно.

Определение 6.2. Дифференциальное уравнение в частных производных называется линейным относительно старших производных, если оно имеет вид

2u

2u

2u

u

u

a

2b

c

F

x, y, u,

,

0,

(6.2)

2

x

y

x

2

x y

1

y

где коэффициенты a,b, c есть функции x и y.

Если коэффициенты a,b, c зависят не только от x и

y, а являются, по-

добно F1, функциями x, y, u,

u

,

u

, то такое уравнение называется квази-

x

y

линейным.

Определение 6.3. Дифференциальное уравнение в частных производных называется линейным, если оно линейно как относительно старших производ-

2u

2u

2u

ных

,

,

, так и относительно функции u и ее первых производ-

x

2

x y

2

y

ных, т. е. имеет вид

a

2u

2b

2u

c

2u

d

u

e

u

gu f ,

(6.3)

2

x y

y

2

x

y

x

44