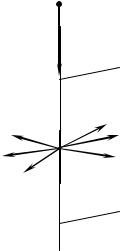
( R – радиус полуокружности). Найти модуль индукции магнитного поля в точке О.

2.Бесконечный провод с током I имеет форму, указанную на рис. 29 ( R – радиус полуокружности). Найти модуль индукции магнитного поля в точке О.

3.Контур с током имеет форму, указанную на рис. 30. Найти модуль индукции магнитного поля в точке О.

4.Конус с основанием радиусом R и высотой h равномерно заряжен электричеством с поверхностной плотностью электрического заряда по боковой поверхности. Найти модуль индукции магнитного поля в центре основания, если конус равномерно вращается вокруг оси симметрии с угловой скоростью ω.

5.Сфера радиусом R равномерно заряжена электричеством с поверхностной плотностью электрического заряда σ. Найти модуль индукции магнитного поля в центре сферы, если она равномерно вращается вокруг оси симметрии с угловой скоростью ω.

6. ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА B

Циркуляция вектора индукции магнитного поля B по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим

	N
контуром, умноженной на μ0:	B dl 0 Ik .
(l )	k 1

Токи входят в алгебраическую сумму со знаком плюс, если с острия тока обход контура выглядит происходящим против часовой стрелки.

Дифференциальная форма закона: B 0 j , где j – плотность тока

проводимости.

Теорема о циркуляции лежит в основе одного из фундаментальных уравнений современной электродинамики. С помощью теоремы о циркуляции вектора магнитной индукции B в некоторых случаях можно относительно просто рассчитать результирующее магнитное поле от протяженных объектов. Методика расчета включает в себя следующие этапы:

1)контур проводят через точку, в которой определяется индукция магнитного поля;

2)контур выбирается с учетом симметрии силовых линий магнитного поля.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. По бесконечному цилиндру радиусом R течет ток, плотность которого является функцией расстояния от оси цилиндра: j(r) = j0∙r. Найти закон зависимости индукции магнитного поля B(r) от расстояния.

41

Решение:

Рассмотрим некоторую точку

внутри цилиндра на удалении r от его

1

оси (рис. 31). Проведем окружность

радиусом r через эту точку. Плоскость

1

окружности перпендикулярна оси цилиндра. Данная окружность совпадает с силовой линией такого же радиуса. Поэтому в любой точке окружности

вектор B1 B r1 будет параллелен

направленному элементу контура dl1 ,

модуль вектора индукции магнитного поля будет постоянной величиной для

j Z

r

1

R

r2

любого

элемента

dl1 :

Рис. 31

B1 dl B1 dl cos 0 B1 dl .

Направление

обхода контура выберем против

часовой

стрелки.

Тогда

вычисление

циркуляции дает

следующее:

B1 dl

B1

dl B1 2 r1 .

Далее находим произведение суммарного тока,

(l1)

(l1)

охватываемого

контуром,

на

магнитную

постоянную:

r

1

2

0 j dS 0

j0

r 2 rdr

0r13 j0 .

Из равенства, выражающего теорему

3

S1

0

о циркуляции, имеем: B r

2

r 3 j

1

r 2 j .

1 0

1

3

0

2 r

3

0 1 0

1

Повторяем процедуру для определения индукции магнитного поля B r2 в некоторой точке внутри цилиндра на удалении r2 от оси цилиндра. Отличие состоит в вычислении суммарного тока, так как ток ограничен окружностью

						R											2
	радиусом R: 0	j dS 0					j0 r 2 rdr												0R3 j0 .						Вычисление циркуляции
	S					0									3
	дает следующее:			B dl B				dl B 2 r2 .												Из			равенства, выражающего
		(l2 )					(l2 )
							B r		2							R3 j					1					R3
	теорему о циркуляции, имеем																		0								j .
																	2 r
							2		3					0							3			0		r	0
																			2						2
	Ответ: B r		1		r 2 j	,	B r		1						R3				j .
									3				0			r
	1	3			0 1 0		2												0
															2

42

Задача 2. Найти модуль индукции магнитного поля внутри тонкого
соленоида с током I = 1 А и плотностью намотки n = 3,14∙103						м –1.
	Решение:
Магнитную	индукцию	поля	бесконечно
длинного соленоида можно вычислить,			используя
теорему о циркуляции. Соленоид представляет собой										B
тонкий провод, навитый плотно виток к витку на					a					b
цилиндрический каркас (рис. 32). Он эквивалентен
системе одинаковых круговых токов с общей прямой					d					c
осью. Бесконечно длинный соленоид симметричен								l
относительно любой плоскости, проведенной через						Рис. 32
его ось симметрии. В любой точке внутри соленоида
вектор B имеет направление, параллельное оси, магнитное поле сосредоточено
внутри соленоида. Возьмем прямоугольный контур				a b c d ,					выберем
обход по часовой стрелке. Циркуляцию вектора				B	можно			представить
следующим образом:

	B dl	B1 dl1	B2 dl2	B3 dl3	B4 dl4 .
(abcd )	(ab)		(bc)	(cd )	(da)

Второй и четвертый интегралы равны нулю, так как вектор B перпендикулярен участкам контура, по которым они берутся. Для этих элементов контура

скалярные произведения обращаются в нуль:				B2 dl2 0, B4 dl4 0 . На
участке c d ,		который является внешним для соленоида, магнитное поле
				l
равно нулю. В итоге получаем			B dl	B1 dl1 B1 dl1 B1 l . Далее
		(abcd )	(ab)	0
вычисляем	правую сторону теоремы. Учитываем, что контур охватывает
		N
суммарный	ток	0 Ik 0 n l I ,	где n –	плотность намотки витков

k 1

соленоида. Приравнивая обе части теоремы, получаем модуль индукции магнитного поля внутри соленоида: B B1 0 n I 4 мТл

Ответ: B 0 n I 4 мТл .

Задача 3. Постоянный ток равномерно распределен по плоскости ХОY так, что модуль его линейной плотности во всех точках плоскости одинаков и

равен j 3,14 Ам (рис. 33). Определить модуль индукции магнитного поля на

высоте 10 см над этой плоскостью, если ток течет в положительном направлении оси ОХ.

43

Решение:

Раccмотрим множество токов, которые текут перпендикулярно оси ОY (рис. 33).

Возьмем		прямоугольный				контур
a b c d , выберем				обход		против
часовой	стрелки.		Циркуляцию вектора B
можно		представить			следующим
образом:
B dl		B1 dl1	B2 dl2		B3 dl3	B4 dl4 .
(abcd )	(ab)		(bc)	(cd )		(da)

		Z
b	B	h	a

	. . . . . . . . . . . . . . . .		Y
–s/2	O		s/2
		B
с	–h	d

	Второй и четвертый интегралы равны нулю,	Рис. 33
	так как в силу произвольности контура

длины сторон можно выбрать:			bc da 0 . Для остальных элементов контура
скалярные произведения имеют вид: B1 dl1				B dl , B3 dl3 B dl . В итоге
						s
					2
для левой	стороны	теоремы	получаем:		B dl 2B dl 2B s . Далее
			(abcd )				s
					2
вычисляем	правую	сторону теоремы. Учитываем, что контур охватывает

N

суммарный ток 0 Ik 0 j s , где n – плотность намотки витков соленоида.

k 1

Приравнивая обе части теоремы, получаем модуль индукции магнитного поля внутри соленоида: B 0 2 j 18,28 мкТл

Ответ: B 0 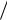2 j 18,28 мкТл

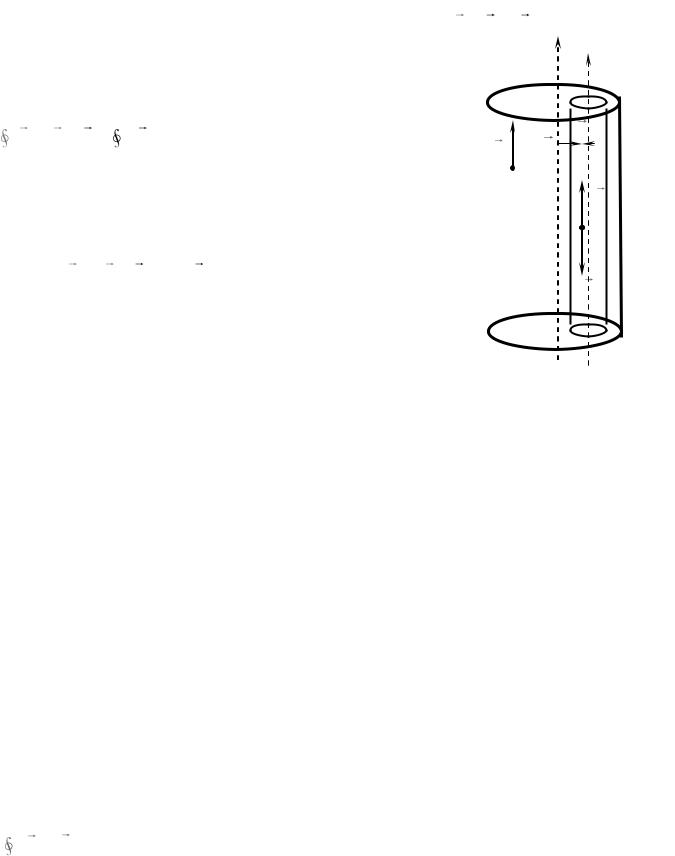
Задача 4. По бесконечному цилиндру течет ток постоянной плотностью j. Цилиндрическая полость размещена так, что ее ось параллельна оси цилиндра и находится на расстоянии s от оси цилиндра. Найти закон изменения модуля индукции магнитного поля внутри полости (рис. 34).

Решение:

Отсутствие тока в полости можно представить как суперпозицию плотностей токов, текущих в противоположных направлениях (рис. 34). Тогда мы имеем

1)один цилиндр с осью OZ , внутри которого течет вверх постоянный ток плотностью j ;

2)второй цилиндр с осью OZ , внутри которого течет вниз постоянный

j .

44

Находим индукцию магнитного поля внутри полости в точке А по

принципу суперпозиции

полей

двух

цилиндров:

B B1 B2 .

Z

Определим модуль индукции B1

от большего цилиндра в точке А,

Z

выбирая обход по окружности радиусом r1 против часовой

стрелки:

r

0

r

1

B1 dl B1

dl B1 2 r1 0 j2 rdr

, B1

jr1 .

j

r

2

2

(l1)

(l1)

0

1

A

Определим модуль индукции B2

от меньшего цилиндра в

j

точке А,

выбирая

обход

по окружности радиуса r2

по

часовой стрелке:

r2

B2 dl B2

dl B2 2 r2

0 j 2 rdr ,

j

(l2 )

(l2 )

0

B 0 jr .

2

2

2

В векторном виде

Рис. 34

B 0 j, r1 и

B 0

j, r2 .

1

2

2

2

Результирующее поле в полости

, B

0 j s .

B B B 0 j, r1

r2

0 j, s

1

2

2

2

0

2

Ответ: B

j s .

2

Задача 5. Постоянный ток I течет по полубесконечному прямому проводнику, а затем растекается радиально симметрично по проводящей плоскости, перпендикулярной проводу. Найти закон изменения модуля индукции магнитного поля: 1) на высоте h над плоскостью и на расстоянии r от проводника; 2) на глубине h под плоскостью и на расстоянии r от проводника (рис. 35).

Решение:

Рассмотрим круговой контур радиусом r, плоскость которого перпендикулярна проводнику и проходит через точку A1 . Используя закон Био–

Савара–Лапласа, легко доказать, что в точке A1 поля от прямого проводника и

от плоскости с током направлены по касательной к выбранному контуру. Выбирая обход контура по часовой стрелке, получаем теорему о циркуляции:

B1 dl B1 2 r 0 I . Правая сторона содержит только ток проводника,

(lA )

1

45

так как токи плоскости не попадают в контур. Для

следующий результат: B

0

I .

1

2 r

Рассмотрим

круговой контур

радиусом

r,

плоскость которого

перпендикулярна

проводнику и

h

проходит через

точку

A2 . В этом

случае ни один не пересекает

поверхность

контура,

поэтому

индукция магнитного поля в этой

точке равна нулю.

Ответ:

B

0

I ,

B 0 .

1

2 r

2

h

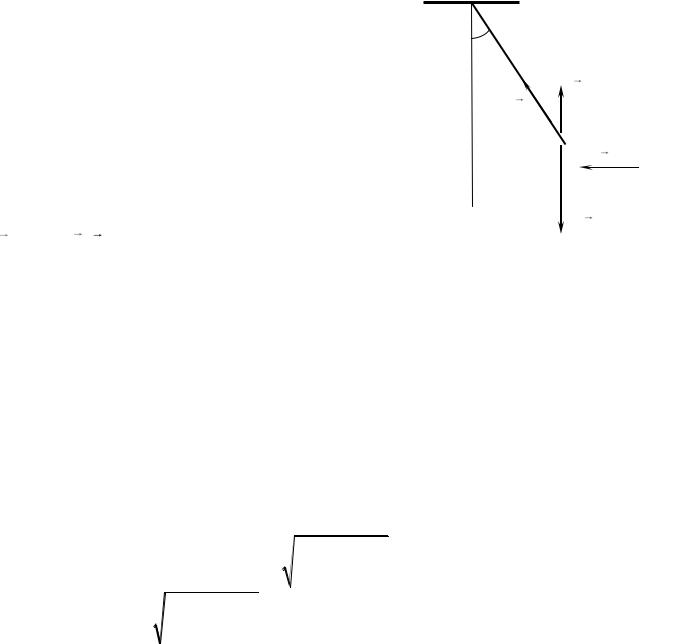
точки A1 получаем

I

A1

r

A2

Рис. 35

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. По бесконечному цилиндру радиусом R течет ток, плотность которого является функцией расстояния от оси цилиндра: j r j0r2 . Найти закон зависимости индукции магнитного поля B r от расстояния r.

2. Бесконечный полый цилиндр радиусом R заряжен электричеством с поверхностной плотностью заряда . Найти модуль индукции магнитного поля как функцию расстояния r от оси цилиндра B r , если он приведен во

вращение с угловой скоростью .

3. Магнитное поле создается токами, равномерно распределенными по двум параллельным проводящим плоскостям. Найти закон изменения модуля индукции магнитного поля между плоскостями и с внешней стороны, если плотности токов имеют одинаковый модуль j , но направлены в противоположные стороны.

4.По обмотке тороида с внутренним радиусом R1 и внешним R2 ,

имеющим N витков, течет ток силой I . Найти модуль индукции магнитного поля как функцию расстояния r от оси симметрии B r .

5.Постоянный ток течет по полубесконечному прямому проводнику, а затем растекается радиально симметрично по проводящей среде, плоскость которой перпендикулярна проводнику. Найти закон изменения модуля индукции магнитного поля: 1) на высоте h над средой и на расстоянии r от проводника; 2) на глубине h в среде и на расстоянии r от проводника.

46

7. СИЛА АМПЕРА. СИЛА ЛОРЕНЦА

ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ

		I , в месте
На элементарный участок dl тонкого проводника с током
нахождения которого создано магнитное поле с индукцией B , со стороны этого
поля действует сила Ампера:
dF	I dl , B .

Вектор dl направлен по касательной к проводнику в направлении тока.

На точечный заряд q , движущийся со скоростью v в электрическом и магнитном полях, действует сила Лоренца:

F qE q v, B .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

dl

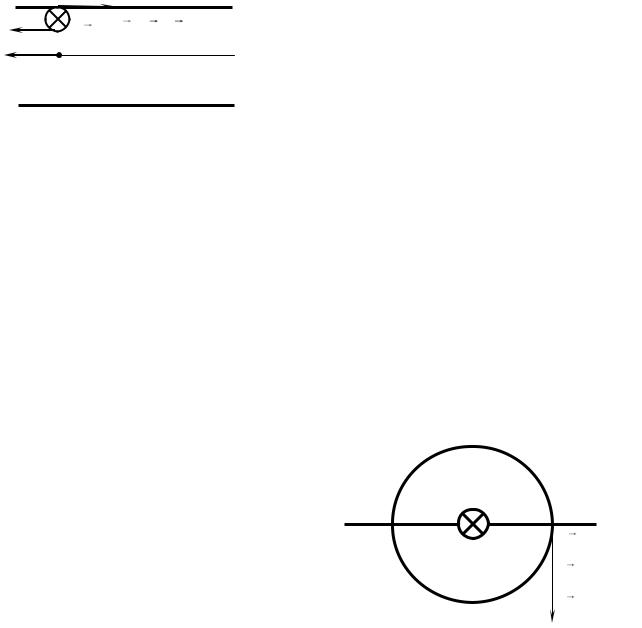
Задача 1. По П-образному проводу,

dF

параллельные

участки

которого

B1 B

0

l

расположены на расстоянии

l 1см друг

от друга, течет ток I = 10 А. Найти силу,

действующую на единицу длины провода

Рис. 36

в точке O (рис. 36).

Решение:

Два параллельных участка провода в точке O создают магнитные поля,

индукция которых одинакова:

B1 B2 .

Оба вектора индукции направлены от

нас в рисунок. Их модули равны

B1

B2

0 I

.

4 l / 2

Третий участок, соединяющий параллельные участки, как видно из

закона Био–Савара, магнитного поля в точке

O не создает. Следовательно,

индукция магнитного поля в точке O направлена в рисунок и ее модуль равен

B B B

0 I .

1

2

l

На участок провода dl действует сила Ампера: dF

I dl , B .

Модуль этой

силы равен

0

I 2

dF

IB dl

dl .

l

Модуль силы, действующей на единицу длины участка, равен

47

	dF			I	2		мН
Fед			0			0,4		.
	dl		l
							м

Задача 2. Тонкий стержень массой m = 11,1 мг и длиной S = 1 см, подвешенный в горизонтальном положении на двух нитях длиной l = 1 м, находится в однородном горизонтальном магнитном поле с индукцией 1 мТл, направленном перпендикулярно стержню (рис. 37). По стержню течет ток I0 = 1

А. Найти период малых колебаний такого стержня.

Решение:

На

рис.

37

провод

расположен

O

перпендикулярно к плоскости рисунка, ток идет от

нас. Воспользуемся уравнением динамики твердого

тела, вращающегося вокруг неподвижной оси OZ :

I

d 2

M izвнешн .

dt 2

Ось

OZ

проходит

через точку подвеса О

перпендикулярно рисунку и направлена на нас.

Момент

инерции

стержня

I ml 2 .

На

стержень

действуют

сила

тяжести

Ампера

mg , сила

F

I

0

d , B ,

сила натяжения нитей T . Моменты

А

этих сил относительно оси OZ равны

Mmgz mgl sin ,

M F z I0SBl sin ,

А

Подстановка этих выражений в уравнение динамики дает

l

FA

T

I

B

mg

Рис. 37

MTz 0 .

	ml2	d 2		mgl sin I						SBl sin .
		dt2							0
	При малых колебаниях можно заменить sin на									. В результате получаем
	динамическое уравнение гармонических колебаний:
			d 2			(mg I	0	SB)
		m									.
			dt2			l

Решениями этого уравнения являются гармонические функции, период колебаний которых определяется выражением

		T		2		ml	6,3 c
					mg	I0SB
Ответ: T 2		ml		6,3 c
		mg I0SB

48

Задача 3. По двум длинным тонким параллельным проводникам (рис. 38) текут постоянные токи I1 = 4 А и I2 = 8 А. Расстояние между проводниками –

a = 2 мм, ширина правого проводника равна b = 4 мм. Имея в виду, что оба проводника лежат в одной плоскости, найти силу магнитного взаимодействия

a

b

между ними в расчете на единицу их длины.

Решение:

x

Разбиваем

широкий

проводник

на

параллельные тонкие полосы. Положение полосы

dx

задается координатой

x , а ее ширина равна

dx . По

полосе протекает ток

dI

2

I2

dx .

Ток I

создает в

b

1

I1

I2

месте нахождения полосы магнитное поле,

модуль

индукции которого равен

Рис. 38

B 0 I1 .

2 x

Вектор B направлен в рисунок. На полосу dx длины h действует сила Ампера,

направленная влево и равная по модулю

dF

I2 dx

0 I1 h .

b

2 x

Сила, действующая на участок широкой полосы длиной h , равна

a b

I I

h

I I

h

b

F

0 1

2

dx

0 1

2

ln

1

.

2 bx

2 b

a

a

Сила взаимодействия, приходящаяся на единицу их длины, равна

F

F

0 I1I2

ln 1

b

1,76

мН

.

ед

h

2 b

a

м

Ответ:

F

0 I1I2

ln

1

b

1,76

мН

.

ед

2 b

м

a

Задача 4. Из начала координат

O

Y

области,

где

созданы

однородные,

параллельные

оси

OY

электрическое

и

E

магнитное

поля

с

напряженностью

E

=

= 10 кВ/м и индукцией B = 1 мкТл (рис. 39),

B

вылетает в направлении оси OX

частица с

удельным

зарядом

q / m

=

1020

Кл/кг.

0

Начальная

скорость

частицы

равна

v0 =

O

X

= 10

7

м/с.

Найти для

нерелятивистского

случая координату

yn

частицы в момент,

Z

когда

она

10

раз

пересечет

ось

OY .

Рис. 39

49

Определить угол между вектором скорости частицы и осью OY в этот момент времени.

Решение:

На частицу со стороны электрического поля действует сила

qE ,

направленная вдоль оси OY . Со стороны

магнитного

поля

действует

сила

q v, B , перпендикулярная оси OY . Под действием электрического поля у

скорости частицы появится компонента, параллельная OY . Разобьем скорость

на две составляющие:

v|| , направленную вдоль полей, и

v , лежащую в

плоскости XOZ , перпендикулярной полям. Скорость частицы равна

v

v|| v .

Проекция уравнения движения частицы

dv

m

qE q v, B

dt

на ось OY

m

dv||

qE .

dt

Следовательно,

v

qEt и y qEt 2

||

m

2m

с учетом начальных условий.

Проекция уравнения движения на плоскость XOZ имеет вид

dv

dv

m

q v||

v , B или m

q v , B .

dt

dt

Последнее уравнение формально описывает движение частицы под действием силы, перпендикулярной скорости и равной по модулю qv B . Такое движение

происходит по окружности с центростремительным				ускорением v2 / R в
соответствии с уравнением
m	v2	qv B .
	R
Вследствие ортогональности силы		q v , B и скорости			v	ее величина не

меняется и равна v v0 . Радиус окружности R постоянен. Частица одновременно движется с постоянной по величине скоростью v по окружности радиусом R и возрастающей со временем скоростью v|| вдоль оси OY . Таким образом,

траектория движения представляет собой спираль на цилиндре, шаг которой возрастает. Частица будет пересекать ось OY через промежутки времени, равные

времени одного оборота проекции частицы на плоскость XOZ :

T 2 R 2 m . v qB

Искомая координата пересечения OY равна

50

y			qE( nT )2			2 2mEn2	0,2 м .
	n					qB2
				2m
Угол между вектором скорости v				и осью OY определяется соотношением

tg

v

v0B

1,6 10

5

.

v

2 En

||

2 2mEn2

v B

1,6 10 5 .

Ответ:

y

0,2 м , tg

0

n

qB2

2 En

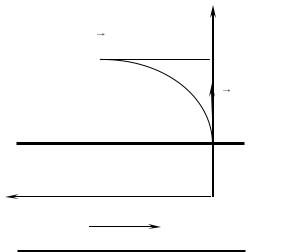
Задача 5. С поверхности цилиндрического провода радиусом a = 1 см,

по которому течет постоянный ток

I = 5 А, вылетает электрон с начальной

скоростью v

= 105 км/с, перпендикулярной

поверхности провода. Найти, на

0

какое максимальное расстояние H удалится электрон от оси провода, прежде чем повернуть обратно под действием магнитного поля тока.

Решение:

Проводник с током создает магнитное поле, модуль индукции которого

равен

B0 I ,

2 y

где y – расстояние от точки наблюдения до оси цилиндра. Над цилиндром

вектор

B направлен на нас перпендикулярно рисунку (рис.

40). На электрон

действует сила, равная ( e) v, B , которая в силу ортогональности B лежит в

плоскости рисунка. Поэтому движение с

Y

учетом

начальных

данных

будет

происходить в плоскости

XOY .

Запишем

B

уравнение движения:

H

i

j

k

0

dv

m

e v, B e

vx

vy

0

.

dt

0

0

B

Проекции на координатные оси приводят к

уравнениям

Z

m

dvx

evy

0 I

,

X

I

dt

2 y

dvy

evx

0 I

Рис. 40

m dt

2 y .

Производная

dvy

dvy

dy

dvy

v

1 dv2y

.

y

dt

dy

dt

dt

2 dy

51

При движении частицы в магнитном поле модуль ее скорости сохраняется:

v2	v2	v2
			или v	x		v2	v2 .
o	x	y				0	y

Подставив два последних выражения в проекцию уравнения движения на ось OY , получим

m dv2y

I

e

v2

v

2

0

.

2 y

2

dy

0

y

После разделения переменных получаем уравнение

m dv2y

e 0 I dy

,

2 y

2

2

2

v0

vy

которое легко интегрируется:

0

m dv2y

H e 0 I dy

,

2 y

2

2

v y 2

v0

vy

a

(при выборе пределов интегрирования мы учли,

что на искомой высоте H

vy 0 ). Выполнив интегрирование, получаем

0

e 0 I

ln y

H

e 0 I

ln

H

.

m v2

v2

или mv

0

0

y

v

2

a

2

a

0

Отсюда находим выражение для максимальной высоты:

H a exp 2 mv0 0,02 м . e 0 I

Ответ: H a exp 2 mv0 0,02 м . e 0 I

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Два одинаковых заряда q = 10–10 Кл, находящихся на расстоянии l = 10 см

5

друг от друга, движутся с одинаковой скоростью 10 м/с. Скорость v перпендикулярна прямой, проходящей через оба заряда. Найти отношение магнитной Fм и электрической Fэ сил, действующих на один из зарядов со

стороны другого.

2. Замкнутый провод имеет форму полуокружности, концы которой соединены диаметром. По проводу течет ток I = 10 А. Найти силу, с которой магнитное поле действует на единицу длины провода в центре диаметра.

52

3. Параллельно бесконечному проводу с током I = 10 А на расстоянии d = 10 см движется заряд q = 10–10 Кл. С какой силой провод действует на

заряд?

4.На двух параллельных рельсах, расположенных под углом к горизонту, в горизонтальном положении лежит стержень длиной l , по которому течет ток I . Найти индукцию вертикального магнитного поля, при которой стержень не скользит по перемычке. Силой трения пренебречь.

5.Квадратная рамка со стороной a лежит в одной плоскости с бесконечным длинным прямым проводом. Две стороны рамки параллельны проводу. Ближайшая из сторон находится на расстоянии d от провода. По проводу течет ток I0 , а по рамке – I . Найти силу взаимодействия провода и

рамки.

8. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

При помещении вещества во внешнее магнитное поле B0 магнитные

моменты отдельных молекул, создаваемые молекулярными токами, стремятся ориентироваться вдоль линий индукции. В результате вещество приобретает ненулевой магнитный момент – намагничивается. Степень его намагничивания характеризуется вектором намагниченности

			1
	J			pm ,
			V

который равен магнитному моменту единицы объема вещества. Для вектора намагниченности справедлива теорема о циркуляции:

(J , dl ) I ,

L

где I – сумма молекулярных токов, охватываемых контуром интегрирования.

Молекулярные токи создают

дополнительное

магнитное

поле

B ,

поэтому

индукция результирующего

Теорема

о

циркуляции

для

поля B B0 B .

вектора напряженности магнитного поля

H

B J

0

включает только токи проводимости

(H, dl ) I.

–

При определенных условиях выполняется соотношение

J H

, где

магнитная восприимчивость. Тогда

B 0 (1

)H 0 H ,

53

где 1 – магнитная проницаемость вещества.

На границе раздела двух магнетиков выполняются граничные условия для нормальных и тангенциальных составляющих полей:

B1n B2n , H1 H2 .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Модуль вектора индукции магнитного поля в вакууме вблизи

плоской поверхности

однородного

изотропного

магнетика

равен

1

мТл,

причем

вектор

B0

B

n

0

составляет угол

с нормалью к поверхности

6

B

(рис. 41). Магнитная проницаемость магнетика

равна = 141. Найти модуль вектора индукции

магнитного

поля

в

магнетике

вблизи

поверхности.

Рис. 41

Решение:

Равенство нормальных составляющих индукции магнитного поля

позволяет определить

Bn B0n B0 cos 0 .

Тангенциальную составляющую магнитного поля определим из равенства

тангенциальных составляющих напряженности магнитного поля:

H H0

B

B0

B B0

B0 sin 0 .

Следовательно, модуль

0

0

вектора индукции магнитного поля равен

B Bn2 B2 B0 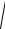cos2 0 2 sin2 0 6 мТл .

Ответ: B B0 cos2 0 2 sin2 0 6 мТл .

Задача 2. Постоянный ток I = 1 А течет вдоль длинного однородного цилиндрического провода круглого сечения радиусом R = 5 см. Провод сделан из парамагнетика с магнитной восприимчивостью = 175. Найти величину

поверхностного молекулярного тока
				Iпов .
			Решение:
В результате намагничивания возникают объемные и поверхностные
молекулярные токи I	и	I	(рис. 42). Для их вычисления воспользуемся
об		пов			L
теоремами о циркуляции		для	H	и J . В качестве замкнутого контура
54

I

пов

	p , H , J , B
Iоб
	m

I

Рис. 42

Итак, по объему провода токи Выделим замкнутый контур L

	выберем окружность	радиусом r R с
	центром на оси цилиндра, лежащую в
	плоскости, перпендикулярной оси. При
	условии r R получим
	H 2 R I , J 2 R Iоб .
	С учетом связи J	H	получаем
	H I / 2 R, Iоб 2 RJ 2 R H I .
I			направлении.
	и Iоб протекают в одном
в	виде окружности радиусом		r R, r R ,

лежащей в плоскости, перпендикулярной оси цилиндра с центром на оси. Контур расположен вне магнетика, поэтому намагниченность во всех точках контура равна нулю. Следовательно, по теореме о циркуляции для J получаем

0 I
		Iоб Iпов .
Поверхностный молекулярный ток равен
			175А .
Iпов I	об I

Знак минус указывает на то, что этот ток течет в обратном направлении по отношению к I .

I 175А .

Ответ: Iпов

Задача 3. Прямой, бесконечно длинный

проводник с током I = 1 А лежит в плоскости

раздела

двух

непроводящих

сред

с

1

I

магнитными проницаемостями 1= 125 и 2 =

=

175. Найти

модуль вектора индукции

H ,

магнитного поля на расстояния r

= 2,65 см от 2

B1,

провода. Иметь в виду,

что линии вектора B

являются окружностями с центром на оси

B2

проводника (рис. 43).

Рис. 43

Решение:

B1 B2 .

В силу граничных условий

Так как

B 0 H ,

то линиями H

будут также окружности. По теореме о циркуляции для вектора H получаем

H1 r H2 r I .

Воспользовавшись соотношениями

H1

B1

B

, H 2

B2

B

,

1 0

1 0

2 0

2 0

получаем, что модуль вектора индукции равен

B1 B2 B

0 1 2 I

1,1мТл .

r( 1 2 )

55

	Ответ: B1 B2	0 1 2 I		1,1мТл .
		r( 1	2 )
	Задача 4. Постоянный магнит имеет вид кольца с узким зазором между
	полюсами. Диаметр середины кольца – d				= 10 см. Ширина зазора b = 1 мм,
	индукция магнитного поля		в зазоре B =		0,8 мТл. Пренебрегая рассеянием

магнитного поля на краях зазора, найти модуль вектора напряженности магнитного поля внутри магнита.

Решение:

Вспомогательный замкнутый контур выбираем в виде окружности

диаметром d , проходящей в середине кольца. В отсутствие макроскопических

токов циркуляция H по выбранному контуру равна нулю:

H1( d b) H2b 0 ,

где H1 – напряженность поля в магните, H 2 – напряженность поля в зазоре.

Так как по условию задачи нам известна индукция в зазоре B , то мы можем определить напряженность магнитного поля в зазоре H2 B / 0 .

Подстановка этого выражения в теорему о циркуляции дает напряженность магнитного поля в магните

H1

Bb

2

А

.

0d

м

Здесь мы опустили знак минус и учли, что d >> b .

Ответ: H1

Bb

2

А

.

0d

м

B

B 0

Задача

5.

Длинный

тонкий

цилиндрический стержень из парамагнетика с

магнитной

восприимчивостью =

175 и

x x dx

0

X площадью поперечного сечения S = 1,21 мм2

Рис. 44

расположен вдоль оси катушки с током. Один

конец стержня находится в центре катушки,

где индукция магнитного поля равна B = 0,1 Тл, а другой конец – в области, где магнитное поле практически отсутствует (рис. 44). С какой силой катушка действует на стержень?

Решение:

Разбиваем цилиндр на небольшие участки длиной dx . Каждый такой участок обладает магнитным моментом

dpm J dV JS dx .

Намагниченность

56

J H	B
		.
	0 (1 )

Магнитное поле в области расположения цилиндра неоднородно. Поэтому на каждый выделенный элемент действует сила, проекция которой равна

dFx dpm dB BS dx dB . dx 0 (1 ) dx

Проекция силы, действующей на весь цилиндр, равна

	l	l	BS dx dB			0	SB dB		SB2
	Fx dF									1,5мН .
			0(1 ) dx				0(1 )		2 0(1 )
	0	0				B

Знак минус указывает на то, что сила направлена влево.

		SB2
Ответ: Fx			1,5мН .
	2 0(1 )
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. В однородное магнитное поле с индукцией						B0 помещена бесконечная
плоскопараллельная		пластина		из	однородного	изотропного	магнетика с
проницаемостью .
		Пластина		расположена перпендикулярно			линиям B0 .
Найти напряженность магнитного поля H в магнетике.
2. Постоянный ток				I	течет вдоль	длинного	однородного

цилиндрического провода круглого сечения радиусом R . Материалом провода является парамагнетик с восприимчивостью . Найти зависимость индукции B от расстояния r до оси провода и плотность тока намагничивания j внутри провода.

3. Индукция магнитного поля в вакууме вблизи плоской поверхности
	с	нормалью		к
магнетика равна B , и вектор B составляет угол			n
поверхности. Магнитная проницаемость магнетика	равна	. Найти	поток

вектора H через поверхность сферы S радиусом R , центр которой лежит на поверхности магнетика.

4.На железном сердечнике в виде тора со средним радиусом R имеется обмотка с общим числом витков N . В сердечнике сделана поперечная прорезь шириной b . При токе I через обмотку индукция магнитного поля в зазоре равна B . Пренебрегая рассеянием магнитного потока на краях зазора, найти магнитную проницаемость железа при этих условиях.

5.Небольшой шарик объемом V из парамагнетика с магнитной восприимчивостью медленно переместили вдоль оси катушки с током из

57

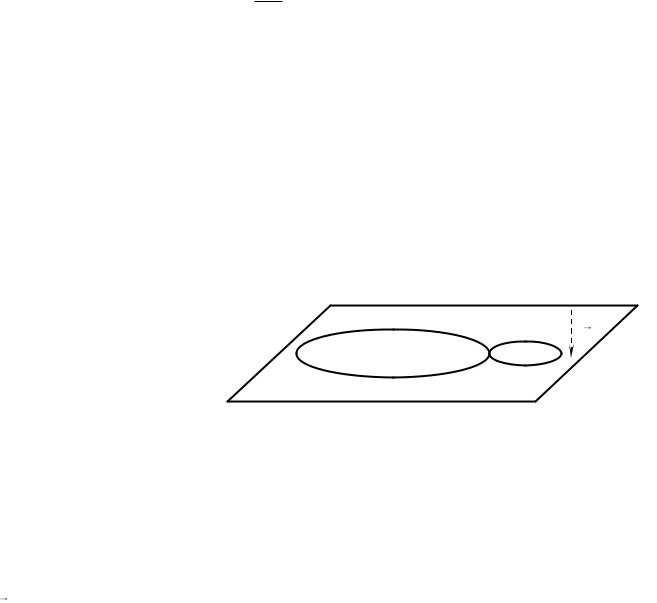
точки, где индукция магнитного поля равна B , в область, где магнитное поле практически отсутствует. Какую при этом совершили работу?

9. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Явление электромагнитной индукции состоит в том, что в замкнутом проводящем контуре при любом изменении магнитного потока, который охватывается этим контуром, возникает электрический ток. Данный ток получил название индукционного, и он связан с величиной ЭДС индукции i

следующим образом: Ii i R .

Закон Фарадея устанавливает, что ЭДС индукции i равна скорости изменения магнитного потока через поверхность, ограниченную контуром,

взятой со знаком минус: i ddt . Знак минус – математическое выражение

правила Ленца о направлении индукционного тока: индукционный ток всегда направлен так, чтобы своим полем противодействовать изменению магнитного потока.

Приведенное выражение для ЭДС индукции контура является совершенно универсальным, не зависящим от способа изменения потока магнитной индукции. Магнитный поток является функцией времени, если хотя бы одна из величин является функцией времени: B = B(t), S = S(t), α = α (t).

Данный факт следует из определения потока вектора:				B cos dS .
			Sп
		ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.	Виток
изолированного	медного			B
провода изогнут	путем
перекручивания	в виде
восьмерки.	Найти
направление		Рис. 45
индукционного	тока в

контуре, если вектор индукции однородного магнитного поля перпендикулярен плоскости контура (рис. 45), а его модуль увеличивается с течением во времени.

Решение:

Обозначим площади контуров как S1 и S2 (рис. 46). Полная ЭДС определяется как алгебраическая сумма ЭДС контуров i1 и i2 . Поток вектора

B с течением времени через площади контуров S1 и S2 растет и создает в контуре индукционный ток, направление которого указан на рис. 46. В

58

соответствии с правилом Ленца этот ток порождает дополнительный

магнитный	поток,
противодействующий			Bi	B
изменению	внешнего
магнитного	потока.		S	S2
Знаки ЭДС i1 и		i2	1
будут	разными,
однако ток	течет	в	Рис. 46

направлении,совпада-

ющем с направлением ЭДС i1 .

Задача 2. Форма проводника описывается уравнением параболы y kx2 . По проводнику движется вверх с постоянным ускорением а горизонтальная проводящая перемычка. Вся конструкция находится во внешнем магнитном поле с индукцией B . Найти зависимость ЭДС индукции от высоты подъема перемычки y, если начальная скорость перемычки равна нулю.

		Решение:
	Пусть перемычка за время dt перемещается вверх из точки с координатой
	y в точку с координатой	y dy . При этом площадь
	прямоугольника на рис. 47 определяется как dS 2xdy .		B	Y
	Из кинематики следует,	что координата y является

функцией времени y a2 t2 . Так как магнитное поле

является постоянным, то поток изменяется вследствие того, что величина площади изменяется во времени. Определим функцию S t :

3

S y

2

y

4

dy

y 2

,

k

3

k

выполняя подстановку

y

a

t2

, получаем

2

3

S t 2

y

2

I

dy

a 2 t3 . Находим ЭДС

k

3

k

индукции из закона Фарадея:

3

dS

2

2 a

By .

B

Ba 2 t2 2

i

dt

k

k

Ответ: i

2

2 a

By .

O

k

y dy

y

X

O

Рис. 47

Y

B

				X
	x	x dx

Рис. 48

59

Задача 3. В магнитном поле, создаваемом длинным прямым проводником с током I , находится квадратная рамка со стороной а. Найти ЭДС индукцииi r как функцию расстояния r между рамкой и проводником. Проводник

находится в одной плоскости с рамкой, вектор скорости рамки v перпендикулярен проводнику с током (рис. 48).

Решение:

На расстоянии x от проводника величина индукции магнитного поля

	определяется как B	1	0		I	. В пределах бесконечно малого прямоугольника
		2			x
	площадью dS adx	модуль индукции магнитного поля практически не

изменяется (см. рис. 48). Находим поток через квадратную рамку, левый край которой находится на расстоянии r от проводника:

r a 1

0

I

I

a

r a

B cos 0 dS

a dx

0

ln

.

2

x

2

r

Sn

r

В соответствии с законом Фарадея находим ЭДС индукции, выполнив подстановку r vt ,

d

d I 0 a

vt a

I 0 a

v

i

ln

dt

2

vt

2

dt

vt a

	Ответ: i	I		0	a2	v	.
		2	r			r a

	v			I 0 a2		v	.
				2 r		r a
	vt

Задача 4. Между полюсами магнита находится небольшая катушка, ось которой совпадает с направлением вектора индукции магнитного поля магнита. Площадь поперечного сечения катушки равна S = 100 см2, число витков – N =

=1000. При переворачивании катушки на 180o через подключенный к ней гальванометр протекает заряд q = 0,2 мКл. Найти модуль индукции внешнего магнитного поля, если сопротивление цепи – R = 100 Ом.

Решение:

Из закона Ома и закона Фарадея находим закон наращивания заряда при изменении потока индукции магнитного поля: i IR ddt , dqdt R ddt ,

dq dR . Так как при перевороте поток изменяется с 1 до 2 , то протекший

60

за это время заряд равен q 1 2 BSN BSN 2 BSN . Отсюда

R R R

находим величину индукции внешнего магнитного поля: B 2qRSN 1мТл .

Ответ: B 2qRSN 1мТл .

Задача 5. Стержень длиной R = 20 см вращают вокруг оси, проходящей через один из его концов в плоскости, перпендикулярной вектору индукции однородного магнитного поля B = 5 мТл, с постоянной угловой скоростью = = 2000 рад/с. Найти разность потенциалов между концами стержня.

Решение:

Находим разность

потенциалов из

закона

Фарадея:

B

dS

.

i

dt

Определим площадь сектора, который

заметает

стержень

за время dt из

пропорции

R2

dS

.

2

d

Тогда получаем

R2

d

R2

B

B

0,2 В .

i

2

dt

2

Ответ: B

R2

0,2 В.

2

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.Найти направление индукционного тока в контуре, если вектор индукции однородного магнитного поля перпендикулярен плоскости контура (рис. 45), а его модуль уменьшается с течением времени.

2.Форма проводника описывается уравнением параболы y kx2 . По

проводнику движется вверх горизонтальная проводящая перемычка с
постоянной скоростью v. Вся конструкция находится во внешнем магнитном поле с
индукцией B . Найти зависимость ЭДС индукции от высоты подъема перемычки y,
		если начальная скорость перемычки равна нулю.
I		3.	В магнитном поле, создаваемом						длинным
		прямым	проводником		с	током		I,	находится
l	v	П-образный		проводник,		по	которому		скользит
		проводящая		перемычка	длиной		l (рис. 49). Найти
		ЭДС индукции i x			как	функцию		расстояния x
		между	перемычкой и проводником. Проводник
Рис. 49
									61