ЦОС лекции

4. Модуль КЧХ | (	)| в полосе непропускания должен удовлетворять
выражению
| (	)|	{	.

Таким образом, коэффициент усиления в полосе пропускания, равный единице, изменяется от (1+ ) до (1– ), а в полосе непропускания – от 0 до

.

Коэффициенты усиления принято выражать в децибелах. В рассматриваемом примере имеем:

– идеальный (необходимый) в полосе пропускания коэффициент усиления равен

дБ;

– максимальный в полосе пропускания коэффициент усиления равен

( ) дБ;

– максимальный в полосе непропускания коэффициент усиления равен

дБ.

Эта величина характеризует минимальное затухание в полосе подавления. Напомним, значение частоты дискретизации определяет полосу частот

входного сигнала ω (	)
Характеристика дискретного фильтра изображена на рисунке 5.3 как
график функции | (	)| от нормированной частоты на промежутке

. Оставшиеся части графика можно восстановить из соображений симметрии (в предположении, что импульсная характеристика ( ) это вещественная последовательность).

Рисунок 5.3 – Спецификация КЧХ дискретного ФНЧ

Для аппроксимации идеального ФНЧ с такими характеристиками реальной системой введен переходный участок ненулевой ширины (

), в котором АЧХ плавно изменяется от значения в полосе пропускания до значения в полосе непропускания.

Имея спецификации фильтра, аналогичные представленным на

рисунке, необходимо определить характеристическую функцию дискретной системы, чья КЧХ удовлетворяет заданным требованиям. Характеристической функцией называют преобразование импульсной характеристики линейной дискретной системы, фактически комплексный коэффициент (собственное значение).

Упражнение 5.1. Изобразить спецификацию КЧХ для дискретного фильтра, соответствующую следующей спецификации непрерывного

фильтра.
1. Частота дискретизации			Гц (	)
2.	Модуль КЧХ фильтра	|	( )| в полосе частот	(	)
(	) должен отличаться от нуля дБ не более чем на			дБ.
3.	Модуль КЧХ фильтра |	(	)| в полосе частот	(	) и
(	) не должен превышать (–50 дБ).

5.1.2.Отличительные особенности цифровых и аналоговых фильтров

1.На аналоговых фильтрах невозможно получить линейную фазовую характеристику. Это означает, что при прохождении сигнала через фильтр изменению подвергается амплитуда и / или фаза входного сигнала. Величина изменения зависит от амплитудной и фазовой характеристики фильтра. Мерой изменения фазовой характеристики служит фазовая или групповая задержка фильтра. Фазовая задержка возникает, когда сигналы разных значений частот составного сигнала проходят через фильтр с разной задержкой. Фазовая задержка определяется как

	( )		( )			( )	,
где ( ) – сдвиг фазы.
На рисунке 5.4 показаны сигналы,			имеющие фазовую задержку, равную

, где	период сигналов.
	1,5
	1	x(t)					x(t- )
	0,5
	0
	-0,5	1	2	3	4	5	6	7	8	9
	-1
	-1,5					t
				Рисунок 5.4

Групповая задержка является мерой средней задержки в фильтре в функции частоты и записывается в виде

( ).

Фильтр имеет линейную фазовую характеристику, если выполняется

равенство

( ) ,

– постоянная величина, выраженная через число интервалов дискретизации. В этом случае фильтр обладает постоянной фазовой и групповой задержкой. Фильтр с нелинейной фазовой характеристикой будет искажать, прошедший через фильтр, сигнал. Это объясняется тем, что частотные компоненты будут задерживаться на величину, не пропорциональную частоте, нарушая их гармоническую связь.

2. Точность аналоговых фильтров ограничена. Точность цифрового фильтра ограничена только длиной используемого слова. Затухание в полосе подавления выше 60 – 70 дБ аналоговым фильтром обеспечить технически сложно.

3. Отфильтрованные данные легко можно сохранить для последующего использования.

4.Цифровые фильтры могут использоваться при очень низких частотах, например, для биомедицинских приложений, где применение аналоговых фильтров приводит к увеличению масса-габаритных показателей.

5.Цифровые фильтры имеют ограничения по быстродействию и

производительности. Наивысшую частоту дискретизации , с которой может работать фильтр, ограничивает время конвертации АЦП и время установления сигнала ЦАП. Скорость работы ЦФ зависит от быстродействия цифрового процессора и числа арифметических операций, которые необходимо выполнить в алгоритме фильтрации. Число арифметических операций повышается, когда требуется получить характеристику фильтра более прямоугольной (сжатой).

6. Цифровые фильтры подвержены шуму АЦП из-за конечной разрядности процесса квантования аналогового сигнала и шуму округления, который вводится при вычислениях.

5.2. Выбор подходящего класса дискретных фильтров

Ранее было показано, что рекурсивные и нерекурсивные ЛДС относятся к классу БИХ и КИХ фильтров. Данные фильтры выполняют вычисление свертки входной последовательности ( ) с последовательностью ( ), значения отсчетов (коэффициенты) которой есть весовые коэффициенты конвольвера. Входной и выходной сигналы БИХ и КИХ фильтров связаны операциями вида

	(	)	∑	(	)	(	), (БИХ фильтр) и
	(	)	∑	(	)	(	), (KИХ фильтр).
Следовательно, фильтр				каждого			типа можно	представить, зная
коэффициенты	его		импульсной				характеристики.	В свою	очередь
коэффициенты	( ) фильтров определяются значениями параметров								и

разностного уравнения

(	) ∑	(	) ∑	(	).
В частности, для	KИХ	фильтров	коэффициентам		( ) соответствуют

значения , а для БИХ фильтра значения коэффициентов его импульсной характеристики зависят от и

Напомним, что для вычисления текущего отсчета выходного сигнала KИХ фильтра используется только текущий и предыдущий отсчеты входного сигнала и не используются выходные. Это приводит к тому, что, если входная последовательность содержит конечное число ненулевых отсчетов, то и отклик содержит последовательность ненулевых отсчетов конечной длительности.

БИХ фильтры принципиально отличаются наличием обратной связи. Каждый выходной отсчет БИХ фильтра зависит от текущего и предыдущего входных отсчетов, а также от предыдущих выходных отсчетов. БИХ фильтр способен выдавать на выход последовательность ненулевых отсчетов бесконечной длины, даже когда все входные отсчеты равны нулю.

5.2.1. Сравнение БИХ и КИХ фильтров

При выборе подходящих классов фильтров руководствуются следующими особенностями КИХ и БИХ фильтров.

1. КИХ фильтры имеет линейную фазовую характеристику, следовательно, КИХ фильтр не вводит фазового искажения в сигнал. Это важно во многих применениях, например, цифровых аудио и видеообработке, биомедицине и пр. Фазовая характеристика БИХ фильтра принципиально нелинейна, особенно на краях полос (см. пример 4.2, рисунки

4.9, 4.10).

2. КИХ фильтры абсолютно устойчивы из-за отсутствия обратной связи. Каковы бы ни были начальные условия, т.е. отсчеты, хранящиеся в линии задержки (памяти), при отсутствии сигнала на входе, когда ( ) , выходной сигнал (свободные колебания) будут отличны от нуля в течение не более, чем тактов.

3.БИХ фильтры требуют меньше операций на один выходной отсчет, чтобы реализовать требуемую частотную характеристику.

4.БИХ фильтры способны обеспечить лучшую фильтрацию при том же количестве операций что и КИХ фильтры.

БИХ фильтр имеет меньшую неравномерность АЧХ в полосе пропускания и более крутую переходную полосу.

Для реализации требуемой спецификации характеристики с КИХ фильтром необходимо иметь большую вычислительную мощность и память, чем в случае ее реализации с БИХ алгоритмом.

Для получения характеристик с высокой прямоугольностью АЧХ, например, полосовых фильтров, требуются КИХ фильтры высокого порядка

–до нескольких сотен и даже тысяч.

5. Аналоговый фильтр легко можно преобразовать в эквивалентный дискретный БИХ фильтр, удовлетворяющий сходным спецификациям.

Учитывая приведенные соображения, обобщенный принцип выбора подходящей структуры фильтра можно свести к следующему.

1.Если основным требованием является «прямоугольность» амплитудно -частотной характеристики и скорость обработки, необходимо применять БИХ фильтры.

2.Если предъявляются повышенные требования к фазовой характеристике – используются КИХ фильтры.

Замечание. Архитектура современных процессоров ЦОС учитывает особенности построения фильтров с конечной импульсной характеристикой.

5.3. Вычисление коэффициентов КИХ фильтра

Целью вычисления коэффициентов (параметров) КИХ фильтра является получение значений ( ), при которых фильтр удовлетворяет спецификации. Разработано несколько методов вычисления значений ( ). Наиболее используемыми из них являются метод «окон», оптимальный метод (по Чебышеву) и метод частотной выборки.

5.3.1. Метод «окон» (вырезания)

Ранее был рассмотрен пример расчета импульсной характеристики идеального ФНЧ по заданной частотной характеристике. Коэффициенты идеальной импульсной характеристики (коэффициенты ряда Фурье) вычислялись по формуле

( )		∫	( )	.	(5.1)
При этом получается бесконечная последовательность коэффициентов					( ).

Хотя значения коэффициентов ( ) уменьшаются с удалением от точки

,	теоретически длительность последовательности ( ) определяется
как	. Формула (5.1) означает физически нереализуемый фильтр. Кроме

того, формула (5.1) определяет коэффициенты БИХ фильтра, но не

коэффициенты	( ) КИХ фильтра. В этом случае комплексная частотная
характеристика	( ) фильтра представляется бесконечным рядом Фурье
	( ) ∑	( )	.	(5.2)

Простейший путь проектирования физически реализуемого фильтра состоит из исключения членов ряда (5.2), имеющих отрицательные значения номера отсчета . Но результатом является все еще импульсная характеристика БИХ фильтра. Для получения характеристики КИХ фильтра

необходимо ограничить ряд (5.2)	сверху до	членов. Тогда получается
усечение идеальной импульсной	характеристики в пределах		.

Таким образом, КИХаппроксимация фильтра состоит в ограничении идеальной в соответствии с выражением

( ) {	( )	их	(5.3)
	ля

Очевидно, отбрасывание коэффициентов сказывается на параметрах КЧХ фильтра. Чем больше коэффициентов остается, тем ближе спектр фильтра к идеальной характеристике.

Прямое усечение ( ) в соответствии с (5.3) равносильно умножению идеальной (требуемой) импульсной характеристики на прямоугольную весовую функцию ( ), называемую прямоугольным окном конечной длины. Тогда требуемая импульсная характеристика записывается как

	(	)	(	) ( )	(5.4)
где	( )	{	ля	их	(5.5)

Вычислим комплексную частотную характеристику КИХ фильтра, если ( ) соответствует выражениям (5.3) и (5.4). Воспользуемся теоремой о

свертке, или модуляции. Фурье-образ от произведения двух
последовательностей	( )	( ) (			) определяется как
( ) ∑	(	)			∑	(	) (	)
				∫	(	) ( (	))	.	(5.6)

Из формулы (5.6) следует, что комплексная частотная характеристика КИХ фильтра определяется периодической сверткой идеальной (требуемой) КЧХ с Фурье-образом окна. Чтобы изобразить графическую интерпретацию свертки (5.6) вычислим Фурье-образ прямоугольного окна.

Пример 5.2. Частотная характеристика прямоугольного окна

вычисляется по формуле
( ) ∑	( )	.	(5.7)

Выражение (5.7) представляет собой сумму членов убывающей геометрической прогрессии

		,
где	– первый член,	– знаменатель прогрессии, – номер взятого
члена.	Сумма первых	членов прогрессии равна

																																																			(5.8)
Если	, формула (5.8) записывается как
																						.																													(5.9)
Так как сумма (5.7) содержит (														) слагаемых, то
				(							)								(						)									(		)										(					)
(	)																								(																										)
																																(															)
Используя формулу Эйлера
получаем																										,
				(				)						( )											(											)
	(	)							(												)																														(5.10)
																)
										(
Замечание. Функция (5.10) известна под названием ядра Дирихле. Как
																																				(										)
видно из	выражения			(5.10),				отношение																	синусов																							дает				модуль
(амплитуду) КЧХ		(		), а показатель степени экспоненты																																														–
фазовый угол (		).

Вычислим значение ядра Дирихле в области определения функции. Модуль ядра Дирихле (или его абсолютное значение) в точке

		(			)
| (	)|	|					|				.	(5.11)

Так как полученному выражению соответствует неопределенность вида ,

применяем правило Лопиталя. Дифференцируем числитель и знаменатель по

( ).

				(			)		⁄	(		)		(				)
| (	)|	|											|						|
						⁄	(			)							⁄
Таким образом, для					получаем максимальное значение |														(	)|
равное	.	Если		значения отсчетов								( )		окна равны					не	единице, а
некоторому , то пиковое значение ядра Дирихле определяется как
										(		).								(5.12)

Вследствие		периодичности		функции | ( )|, значения (5.12)
формируются также на частотах, кратных частоте дискретизации
Далее оценим ширину главного лепестка Фурье-образа окна. Первый
ноль |	(	)| возникает на частоте,		на которой аргумент числителя функции
| (	)| равен , т.е. когда
		(		)

Нормированное значение частоты в этом случае равно

Ширина главного лепестка Фурье-образа окна соответствует величине

Точки области частот, в которых ядро Дирихле равно нулю определяются из

Ширина всех боковых лепестков одинакова равна

										.
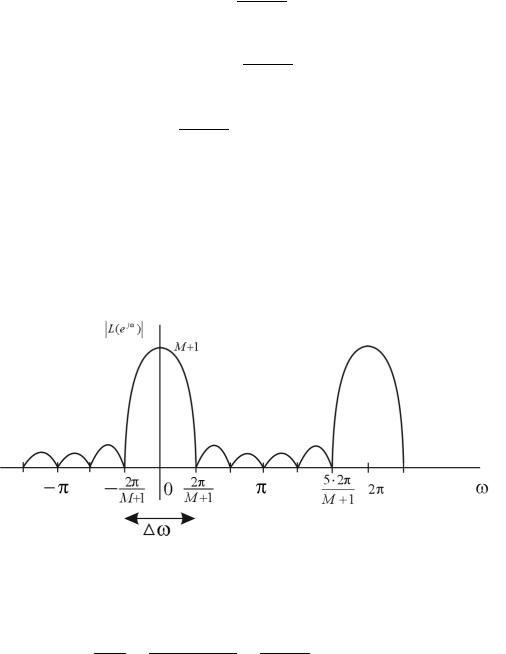
На рисунке 5.5	изображен			график модуля комплексной частотной
	(			)
характеристики | (	)| |							| прямоугольного окна для

Рисунок 5.5 –Модуль Фурье-образа прямоугольного окна

Если частотная ось представляется в герцах, то нулевым точкам Фурьеобраза прямоугольного окна соответствует нормированная частота

( )

где – обозначает нормированную круговую частоту. Например, для окна

длиной	,	Гц нулевым точкам Фурье-образа соответствуют
значения частот (		)	{	} Гц.

С увеличением ширина главного и боковых лепестков уменьшается и увеличивается число пульсаций. Амплитуды боковых лепестков уменьшаются по мере удаления от главного лепестка. Но как бы ни велико было значение , амплитуда боковых лепестков никогда не становится равной нулю.

Замечание. Нежелательные пульсации амплитудно-частной характеристики в полосе пропускания и небольшое ослабление в полосе непропускания сравнительно простых фильтров обусловлены боковыми лепестками Фурье-образа прямоугольного окна.

На рисунке 5.6 показаны графики функций ( ( )), ( ) и процесс формирования периодической свертки (5.6) идеальной (требуемой) КЧХ с Фурье-образом прямоугольного окна, т.е.

( ) ∫ ( ) ( ( )) .

а) процесс свертки

б) аппроксимация идеальной характеристики		(	)
Рисунок 5.6 – Графики Фурье-образов	( ) (	(	)) (	)
Анализируя полученную свертку в	частотной	области		идеальной

прямоугольной функции ( ) с ядром Дирихле, видим, что колебания

функции ( ) попадают в область частотного прямоугольника ( ). Свертка точно воспроизводит эти колебания, рисунок 5.6 б. Вблизи точек разрыва идеальной прямоугольной функции ( ), т.е. для значния появляются пульсации, максимум которых слева и справа составляет

от АЧХ и остается таковым вне зависимости от значения	окна.
Таким образом, усечение числа коэффициентов	( ) ряда Фурье
приводит:

–к появлению выбросов результирующей функции ( ) в окрестностях точек разрыва (на границах полос пропускания и непропускания);

–к неравномерности результирующей АЧХ на всем периоде.

Говорят, что свертка ( ) ( ) осциллирует. Имеет место так называемый эффект Гиббса.

Как видно из рисунка 5.6 частотная характеристика КИХ фильтра это

размытая версия идеальной прямоугольной функции		(	). Если	Фурье-
образ окна (	) является узким, т.е. сконцентрирован		в узкой	полосе
частот, то КЧХ	( ) будет подобной идеальной (	) почти повсюду, за

исключением ее точек разрыва.

При выборе окна руководствуются следующими требованиями:

– окно должно быть достаточно коротким, чтобы минимизировать объем вычислений при реализации фильтра;

– Фурье-образ окна	(	) должен быть сконцентрирован в узкой полосе
частот, чтобы свертка	(	) ( ) как можно точно воспроизводила

заданную (идеальную) частотную характеристику фильтра;

– ширина переходной полосы фильтра определяется значением ширины основного лепестка весовой функции ( );

– неравномерность частотной характеристики фильтра в полосах пропускания и подавления определяется боковыми лепестками весовой

функции	( ).
Эти требования являются противоречивыми. При увеличении числа
отсчетов	импульсной характеристики		( ) амплитуды главного и боковых
лепестков	растут, а ширина		главного и ширина		боковых

лепестков уменьшается; площадь, которую они ограничивают, остается постоянной. Пульсации сжимаются по горизонтали к вертикальному отрезку, проведенному в точке . Осцилляция становится более резкой. Так как площадь, под каждым лепестком остается постоянной, то при увеличении числа отсчетов импульсной характеристики ( ) колебания будут неуменьшающимися по амплитуде.

Из теории рядов Фурье известно, что неравномерность функции, приводящая к эффекту Гиббса, может быть уменьшена, если использовать менее резкое усечение коэффициентов ряда Фурье. Сглаживая вертикальные границы окна, можно уменьшить высоту боковых лепестков. Однако, это