ЦОС лекции

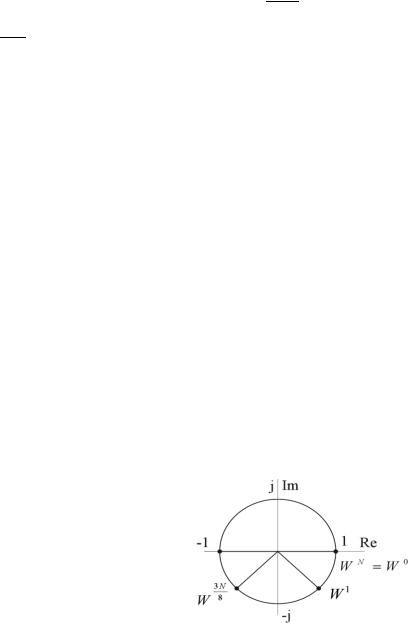
Величина полной фазы за дискретное время определяется как

( )

где ( ) – скорость изменения фазы ДЭФ или частота этой функции. Таким

образом, частота ДЭФ – это число оборотов, совершаемых вектором ДЭФ на интервале ее определения

Пример 6.3. Вычисление значений ДЭФ.

1.

Решение.			(					)		(		)	√					√
2.
Решение.
3.
Решение.			(						)	(		)
4.
	(				)		(					)
Решение.
(			)										√					√

На рисунке 6.2 показаны положения вектора ДЭФ на комплексной плоскости примера 6.3.

Рисунок 6.2 – Положение вектора ДЭФ
Систему ДЭФ записывают в виде матрицы	строки которой

нумеруются переменной столбцы переменной . В пересечении k-й строки и -го столбца записывается величина :

.

[

]

Например, для	матрица	имеет следующий вид:
	[	].	(6.3)
Если подставить в эту матрицу числовые значения степенного ряда			, то
получим
	[	].	(6.4)

На рисунке 6.3 показаны положения вектора ДЭФ и ее значения на комплексной плоскости, соответствующие матрице (6.4).

Рисунок 6.3 – Функции ДЭФ для

6.1.1. Свойства дискретных экспоненциальных функций

1. Функции (		) ортогональны, т.е.
	∑	(	)	{	е ли
					е ли
Так как (	)	, то
	∑		{		е ли
					е ли

Следствием свойства ортогональности является:

–скалярное произведение различных двух строк матрицы которых должна быть комплексно сопряженной, равно нулю;

–скалярное произведение одинаковых двух строк матрицы

которых должна быть комплексно сопряженной, равно .

(6.5)

,одна из

,одна из

Действительно,	(	)				Сумма	единиц даст число
Матричная запись свойства ортогональности имеет вид
			,				(6.6)

где	– единичная матрица.
	2. Периодичность:
если	то
	.	(6.7)

Поскольку ДЭФ являются периодическими функциями, матрицу (6.3) можно

переписать с минимальными фазами (( )) ,		образующимися после
вычитания из значения целого числа периодов		т.е.
	.
Для	матрица ДЭФ (6.3) с минимальными фазами

[

]

3. Симметричность.

ДЭФ является функцией двух переменных и Выводы относительно одной из переменных справедливы и для другой. Тогда

4. Обратная матрица ДЭФ.

Из свойства ортогональности . Умножим обе части этого равенства слева на

							.	(6.8)
5. Мультипликативность:
– по строкам	(	)		(		)	(	)
– по столбцам	(	)		(		)	(	)
							(	)
Действительно,								. При умножении любых двух
строк (столбцов) матрицы				получается строка (столбец) той же матрицы.

Номер полученной строки (столбца) равен сумме номеров сомножителей.

6.2. Определение дискретного преобразования Фурье

Прямое дискретное преобразование Фурье (ДПФ) последовательности ( ) определяется как дискретная последовательность ( ) в частотной

области (экспоненциальная форма)

( ) ∑	( )		∑	( )	(6.9)

где – индекс ДПФ в частотной области, – индекс временной входной последовательности отсчетов сигнала.

Дискретное преобразование Фурье устанавливает связь между временным и частотным представлением сигнала при разложении его по конечным дискретным экспоненциальным функциям.

	Обратное ДПФ (ОДПФ) имеет следующий вид:
( )	∑	( )	∑	( )	(6.10)

Взаимная обратимость выражений (6.9) и (6.10) доказывается подстановкой

( ) в ( ) т.е.
(	)	∑	(∑	( )	)	(6.11)
Так как ( ) не зависит от		, изменяем порядок суммирования в (6.11),
(	)	∑	( ) ∑			(6.12)

Всилу ортогональности ДЭФ внутренняя сумма отлична от нуля только при

Вэтом случае правая часть выражения (4.24) равна

( )

(

)

Тригонометрическая форма ДПФ:

–

прямое ДПФ

(

)

∑

(

) (

)

–

обратное ДПФ

(

)

∑

( ) (

)

Замечание. Принципиальное различие между дискретизированным по времени преобразованием Фурье и ДПФ обусловлено характером системы

функций {	̂		} и {		}, а именно:
– огибающая дискретных значений функции										соответствует
функции	̂
– конечный интервал времени [							] задания функции				;
– периодической структурой отсчетов восстанавливаемой
последовательности		(	)	(		)
6.3. Свойства дискретного преобразования Фурье
1. Периодичность.			Свойство			периодичности				ДЭФ
приводит к выражениям
	(	)		(	) и	(		)	(	)
Действительно, (			)	∑		( )	(	)	∑	( )	( )

Обычно ограничиваются рассмотрением одного периода длиной во временной и в частотной области. Это позволяет определить матричную форму ДПФ:

– прямое ДПФ

где

[

( ) ( )

(

)]

и

[ ( )

(

)

(

)]

– векторы

отсчетов

последовательности спектральных

коэффициентов

и

сигнала

соответственно;

– обратное ДПФ

.

Используя формулу (4.20), получаем

.

2. Линейность. Класс линейных систем определяется линейными

операциями или принципом суперпозиции. Если

(

) и

( )

входные

последовательности,

а

(

) и

(

) соответственно их ДПФ, то при подаче

на

вход

последовательности

(

)

( )

(

)

систему называют

линейной тогда и только тогда, когда выполняется

(

)

(

)

(

)

где

и

произвольные

постоянные параметры

(константы).

Спектр

последовательности

(

) равен

( ) ∑( ( )

( ))

∑ ( )

∑ ( )

(

)

(

)

3. Инвариантность ДПФ относительно сдвига по времени и частоте:

1. Инвариантность относительно циклического сдвига по времени. Если

последовательность

(

)

имеет

ДПФ

( ),

то

ДПФ

последовательности

(

) равно

(

)

(

)

Рассмотрим две последовательности

(

) и

(

)

(

)

. Формы

последовательностей показаны на рисунке 6.4а,б.

а)

x(n)

n

x(n-h)

б)

h

n

Рисунок 6.4

ДПФ последовательности

( )

(

) равно

(

)

∑(

)

(

)

.

Заменяя индекс

суммирования

и

введя

новую

переменную

,

получим

(

)

(

)

( )

∑

( )

(

)

∑

( )

( )

где

(

)

(

). Тогда

(

)

( )

| ( )|

(

)

| ( )|

| ( )|

Таким образом, при сдвиге дискретного сигнала по времени изменениям подвергаются только фазы дискретных функций (фазовый спектр), амплитудный спектр не изменяется.

2. Инвариантность относительно сдвига по частоте. Если спектральной последовательности ( ) соответствует последовательность ( ) то при сдвиге последовательности ( ) исходная последовательность ( ) получит фазовый сдвиг, т.е.

( )

( )

Пусть

( )

(

) Обратное ДПФ последовательности (

) равно

(

)

∑(

)

(

)

.

Заменяя

индекс

суммирования

, и

введя

новую

переменную

,

получим

(

)

(

)

( )

∑

( )

(

)

∑

( )

( )

где

(

)

(

).

4. Теорема о свертке. Если исходные последовательности отсчетов сигналов ( ) и ( ) имеют конечные периоды , их циклическая свертка определяется формулой

		( )	∑	(	) (	),	= 0, 1,…,		–1.
Вычислим ДПФ последовательности (							)
(	)	∑	(	)	∑	∑	( )	(	)	(6.13)
Так как	(	) не зависит от			, изменяем порядок суммирования в (6.13).
			(	) ∑	(	) ∑	(	)	.	(6.14)

Используя свойство инвариантности относительно циклического сдвига по времени, можно записать составляющую выражения (6.14) как

∑	(	)		( )
Тогда
( )	∑	( )	( )	( ) ( )	(6.15)

Таким образом, спектр свертки равен произведению спектров сворачиваемых последовательностей. Коэффициенты свертки вычисляются на основе ОДПФ по формуле

( ) ∑ ( )

Теорема (6.15) позволяет вычислить коэффициенты свертки при помощи ДПФ по формуле

( ) { ( ) ( )}.

При больших величинах на практике применяют эффективные алгоритмы вычисления свертки с использованием быстрых преобразований Фурье.

5. Теорема о корреляции. По определению (2.13)									корреляционная
функция двух конечных последовательностей						(	)и ( ) равна
	( )	∑	(	) (	), для		= 0, 1,…,		–1.
Вычислим ДПФ последовательности (					)
(	) ∑	( )		∑	∑	(	) (	)	(6.16)
Так как (	) не зависит от		, изменяем порядок суммирования в (6.16).
	( )	∑	(	) ∑	(		)	.	(6.17)

Используя свойство инвариантности относительно циклического сдвига по времени, можно записать составляющую выражения (6.17) как

∑	(	)	(	)
Тогда
( )	∑	( )	( )	( ) ( )	(6.18)

Таким образом, спектр корреляционной функции равен произведению спектров сворачиваемых последовательностей, причем один из спектров берется в комплексном сопряжении.

Коэффициенты корреляционной функции вычисляются на основе ОДПФ по формуле

( )

∑

( )

Теорема (6.18) позволяет вычислить коэффициенты корреляционной функции при помощи ДПФ по формуле

( )

{

( )

( )}.

На практике применяют эффективные алгоритмы вычисления корреляционной функции с использованием быстрых преобразований Фурье.

6. Теорема Парсеваля. Пусть последовательности ( ) и ( ) будут идентичными. В этом случае теорема о корреляции записывается как

( ) ( ) ( ) | ( )| .

Коэффициенты корреляционной функции, вычисляются на основе выражения ОДПФ, т.е.

	(	)	∑	(	)			∑		| ( )|
			∑		(	) (		)			(6.19)
В частном случае, для			равенство (6.19) сводится к соотношению
( )	∑	| ( )|				∑	| ( )|		∑	(	) ,
			∑	|	(	)|	∑	(	)		(6.20)

Из (6.20) следует, что энергия сигнала, вычисленная во временной области (по переменной ) равна энергии сигнала, вычисленной в частотной области. Каждая величина | ( )| представляет собой мощность дискретной гармоники, имеющей частоту с номером .

7. Быстрое преобразование Фурье

Быстрый алгоритм Фурье позволяет эффективно вычислять дискретное преобразование Фурье (ДПФ). При этом сокращается количество выполняемых операций, а также объем памяти, необходимый для вычисления ДПФ. В результате многие прикладные задачи спектрального анализа, обработки сигналов за счет уменьшения вычислительной сложности решаются в реальном времени.

7.1. Вычислительная сложность дискретного преобразования Фурье

Прямое и обратное ДПФ определяются по формулам

(	)	∑	(	)						(7.1)
(	)	∑	(	)						(7.2)
Последовательность			( )	( (	)	(	)	(	)) это отсчеты сигнала, а
последовательность			( )	(	(	)	( )	(	))	это отсчеты

дискретного спектра. Равенства (7.1) и (7.2) представляют собой экспоненциальную форму записи ДПФ. Можно записать ДПФ в матричной форме:

,

,

где

[

(

) ( )

(

)]

[

(

) ( )

(

)]

– векторы

столбцы отсчетов сигнала и спектральных коэффициентов.

Если

(

) комплекснозначная последовательность, то для вычисления

одного отсчета ДПФ потребуется

умножений и

сложений комплексных чисел.

Пример 7.1. Вычислить преобразование Фурье длиной

Решение. Ядро прямого преобразования

[

]

[

].

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

[

] [

( )]

( )

( )

( )

( )

[ ( )]

( )

[ ( )

( )

( )

( )]

( )

Пусть

и

комплексные числа, где

√ .

Сумма этих чисел

равна

(

)

(

).

Умножение этих чисел равно