Pract_tv

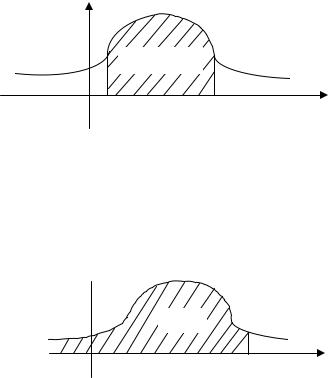
р(х)

Р(а≤Х≤ b)

а

b

х

Рис. 8.1

3.F (x)= ∫x p(x)dx (рис. 8.2).

−∞

р(х)

F(х)

х х

Рис. 8.2

4. +∞∫ p(x)dx =1.

−∞

Геометрически свойства плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Пример 8.1. Минутная стрелка электрических часов передвигается скачками поминутно. Вы бросили взгляд на часы. Они показывают а минут. Тогда для вас истинное время в данный момент будет случайной величиной. Найти ее функцию распределения.

Решение. Очевидно, что функция распределения истинного времени равна 0 для всех x ≤ a и единице для x > a +1. Время течет равномерно. Поэтому вероятность того, что истинное время меньше а + 0,5 мин, равна 0,5, так как одинаково вероятно, прошло ли после а менее или более полминуты. Вероятность того, что истинное время меньше а + 0,25 мин, равна 0,25 (вероятность этого времени втрое меньше вероятности того, что истинное время больше а + 0,25 мин, а сумма их равна единице, как сумма вероятностей противоположных событий). Аналогично рассуждая, найдем, что вероятность того, что истинное время меньше а + 0,6 мин, равна 0,6. В общем случае вероятность того, что истинное время меньше а +

81

+ α мин (0 < α <1), равна α. Следовательно, функция распределения истинного времени имеет следующее выражение:

0 для x ≤ a,

F(x)= α для x = a + α (0 < α ≤1),1 для x > a +1.

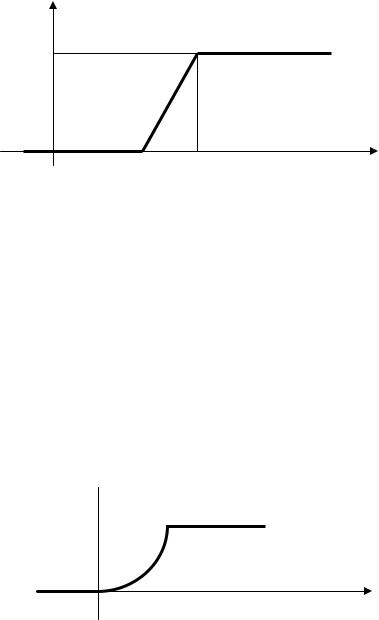
Она непрерывна всюду, а производная ее непрерывна во всех точках, за исключением двух: х = а и х = а + 1. График этой функции имеет вид (рис. 8.3):

F(х)
1
а	а+1	х
	Рис. 8.3

Пример 8.2. Является ли функцией распределения некоторой случайной величины функция

0 при x ≤ 0,

F (x)= x3 при 0 < x ≤1,1 при x >1.

Решение.

F(х)

1

1

х

Рис. 8.4

82

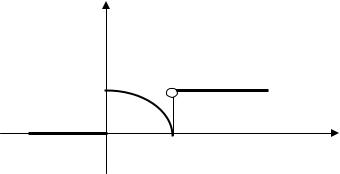
Все значения этой функции принадлежат отрезку [0;1], т.е. 0 ≤ F(x)≤1. Функция F(х) является неубывающей: в промежутке (− ∞; 0] она постоянна, равна нулю, в промежутке (0;1] возрастает, в промежутке (1; + ∞) также постоянна, равна единице (см. рис. 8.4). Функция непрерывна в каждой точке х0 области ее определения — промежутка (− ∞; + ∞), поэтому непрерывна слева, т.е. выполняется равенство

lim F(x)= F(x0 ), F(x0 − 0)= F(x0 ).

x→x0 −0

Выполняются и равенства:

lim F(x)= 0,	lim F(x)=1.
x→−∞	x→+∞

Следовательно, функция F (x) удовлетворяет всем свойствам, характерным для функции распределения. Значит данная функция F (x) является функцией распределения некоторой случайной величины Х.

Пример 8.3. Является ли функцией распределения некоторой случайной величины функция

0 при x ≤ 0,

F(x)= cos x при 0 < x ≤ π / 2,1 при x > π / 2.

Решение. Данная функция не является функцией распределения случай-

ной величины, так как на промежутке		0;	π		она убывает и не является
			2

непрерывной. График функции изображен на рис. 8.5.

F(х)

1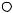

π/2

х

Рис. 8.5

83

Пример 8.4. Случайная величина Х задана функцией распределения

0 при x ≤ 0,

F (x)= ax3 при 0 < x ≤ 2,

1 при x > 2.

Найти коэффициент а и плотность вероятности случайной величины Х. Определить вероятность неравенства 0 < X <1.

Решение. Плотность распределения равна первой производной от функции распределения

				0 при x ≤ 0,
	′						2	при 0 < x ≤ 2,
p(x)= F		(x)= 3ax
				0 при x > 2.
Коэффициент а определяем с помощью равенства
		2
		∫3ax2dx =1,
отсюда		0
a =		1			=			1					=	1 .
	2										2
			2	dx		3		1	x	3				8
	3∫x							3			0
	0

Тот же результат можно было получить, используя непрерывность функции F (x) в точке x = 2

lim F (x)	= lim ax3	=8a ,	lim F (x)=1.
x→2−0	x→2−0		x→2+0
Следовательно, 8a =1	a = 1 .
	8

Поэтому плотность вероятности имеет вид

0 при x ≤ 0,

3

p(x)= 8 x2 при 0 < x ≤ 2,

0 при x > 2.

Вероятность P(0 < X <1)попадания случайной величины Х в заданный промежуток вычисляется по формуле

P(0 < X < 1) = F(1) − F(0) = 18 − 0 = 18 .

84

Пример 8.5. Случайная величина Х имеет плотность вероятности (закон Коши)

	p(x)=	a	(− ∞ < x < +∞).
		1 + x2

Найти коэффициент а и вероятность того, что случайная величина Х примет какое-нибудь значение из интервала (0; 5). Найти функцию распре-

деления этой случайной величины.

Решение. Найдем коэффициент а из равенства

+∞∫ 1 +ax2 dx =1,

−∞

но +∫∞	a	dx = a+∫∞		dx			= aarctgx		+ ∞
−∞1 + x2			−∞1 + x2						− ∞
Следовательно, a =					1 .
				1	π
Итак,		p(x)=					.
			π(1 + x2)

=a[arctg(+ ∞)− arctg(− ∞)]= a π + π = aπ.

2 2

Вероятность того, что случайная величина Х примет какое-нибудь значение из интервала (0; 5), равна

P(0 < X <5)=

5

dx

1

5

1

(arctg5 − arctg0)=

1

0∫

π(1 + x2)

=

π arctgx

0 =

π

π arctg5 ≈ 0,435.

Найдем функцию распределения данной случайной величины

F(x)= ∫x

dx

= 1 arctgx

x

= 1

(arctgx −arctg(−∞))= 1 arctgx + π = 1

+ 1 arctgx.

2

−∞ π(1+ x )

π

−∞

π

π

2 2 π

Пример 8.6. График плотности вероятности случайной величины Х изображен на рис. 8.6 (закон Симпсона). Написать выражение плотности вероятности ифункцию распределения этой случайной величины.

р(х)

1

–1

0

1

х

Рис. 8.6

85

Решение. Пользуясь графиком, записываем аналитическое выражение плотности распределения вероятностей данной случайной величины

0 при x ≤ -1и x >1, p(x)= x +1при −1 < x ≤ 0,− x +1 при 0 < x ≤1.

Найдем функцию распределения.

Если x ≤ −1, то F (x)= ∫x p(x)dx = ∫x

0 dx = 0.

−∞

−∞

x

−1

x

2

Если −1< x ≤ 0 , то F (x)= ∫ p(x)dx = ∫0 dx +∫(x +1)dx =

(x +1) .

−∞

−∞

−1

2

Если 0 < x ≤1, то F(x)=

∫x p(x)dx =−∫10 dx + 0∫

(x +1)dx + ∫x (1− x)dx =

−∞

−∞

−1

0

=

(x +1)2

0

−

(1 − x)2

x

=

1

−

(1 − x)2

1

=1 −

(1 − x)2

.

2

−1

2

0

2

2

+

2

2

Если x >1, то F(x)= ∫x p(x)dx =−∫10 dx + 0∫(x +1)dx + 1∫(1 − x)dx + ∫x 0 dx =

(x +1)2

0

(1 − x)2

1

−∞

−∞

−1

0

1

=

−

= 1

+

1

=1.

2

−1

2

0

2

2

Следовательно, функция распределения имеет вид

0 при x ≤ −1,

(x +1)2

при −1< x ≤ 0,

F(x)=

2

(1 − x)2

1 −

2

при 0 < x ≤1,

1 при x >1.

Задачи для самостоятельного решения

8.1. Дана функция

0, если x ≤ − π2 ,

F(x)= cos x, если − π2 < x ≤ 0,

1, если x > 0.

86

Показать, что данная функция является функцией распределения некоторой случайной величины Х. Найти вероятность того, что эта случайная величи-

на принимает значения из интервала − π ; 0 .

3

Ответ: 12 .

8.2. Дана функция

0, если x ≤ 0,

F (x)= x2 , если 0 < x ≤ 2,

1, если x > 2.

Является ли она функцией распределения некоторой случайной величины?

Ответ: нет.

8.3. Является ли функцией распределения некоторой случайной величины функция

	F(x)=	1	(− ∞ < x < +∞)?
		1 + x2

Ответ: нет.

8.4. Является ли функцией распределения некоторой случайной величины каждая из следующих функций:

а) F (x)= ex при x ≤ 0,

1при x > 0.

б) F (x)= e−xx при x ≤ 0,

e при x > 0.

Ответ: а) да; б) нет.

8.5. Дана функция распределения случайной величины Х:

0 при x ≤ 0,

x2

F (x)= 4 при 0 < x ≤ 2,

1 при x > 2.

87

Найти плотность вероятности, а							также вероятности P(X =1), P(X <1),
P(1≤ X < 2).
0 при x ≤ 0 и при x > 2,
Ответ: p(x)= x		при 0 < x ≤ 2.
	2
P(X =1)= 0; P(X <1)= 1						; P(1 ≤ X < 2)= 3 .
			4				4
8.6. Случайная величина Х,				сосредоточенная на интервале [−1; 3], задана
функцией распределения F(x)=			1 x +			1	. Найти вероятность попадания случай-
			4			4
ной величины Х в интервал [0; 2]. Построить график функции F(х).
Ответ: P(0 ≤ X ≤ 2)= 1 .
		2
8.7. Случайная величина Х, сосредоточенная на интервале [2; 6], задана
функцией распределения F(x)=				1	(x2		− 4x + 4). Найти вероятность того, что
			16

случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

Ответ: P(2 ≤ X < 4)= 14 ;P(2 ≤ X < 6)=1;P(3 ≤ X ≤ 6)= 1615 ; P(6 ≤ X ≤ 6)= 0 .

8.8. Случайная величина Х, сосредоточенная на интервале (1; 4), задана

квадратичной функцией F(x)= ax2 + bx + c , имеющей максимум при х = 4. Найти параметры а, b, с и вычислить вероятность попадания случайной величины Х в интервал [2; 3].

Ответ: a = −	1	;	b =	8	;	c = −	7	;	P(2 ≤ X ≤3)=	1 .
	9			9			9			3

8.9. Функция распределения случайной величины Х имеет вид

0 при x < −1,

F (x)= a + barcsin x при −1≤ x ≤1,

1 при x >1.

88

Определить постоянные а и b. Найти плотность вероятности случайной величины Х и построить ее график.

1

1

1

при

x

<1,

Ответ: a =

b =

p(x)=

π

;

;

1− x2

2

π

x

≥1.

0 при

8.10. Плотность распределения вероятностей случайной величины Х определяется функцией

p(x)= ax2e−kx (k > 0, 0 ≤ x < +∞).

Найти значение коэффициента а. Найти функцию распределения F(х) величины Х.

Ответ: a = k3	;	F(x)=1 − k2x2 + 2kx + 2 e−kx .
2		2
8.11. Функция р(х) задана в виде
		0 при x ≤1,
		p(x)= a			при x >1.
				4
		x

Найти значение постоянной а, при которой функция будет плотностью вероятности некоторой случайной величины Х; функцию распределения F(х); вычислить вероятность того, что случайная величина Х примет значение на отрез-

ке [2; 3].

0 при x ≤1,					19
Ответ: a = 3; F(x)=	1			P(2 ≤ X ≤ 3)=		.
			при x >1,
1−					216
	x	3

8.12. Задана плотность распределения непрерывной случайной величины Х:

0 при x ≤ π / 6,

p(x)= 3sin3x при π / 6 < x ≤ π /3,0 при x > π /3.

Найти функцию распределения F(х).

0 при x ≤ π / 6,

Ответ: F(x)= − cos3x при π / 6 < x ≤ π /3,1 при x > π /3.

89

8.13. Плотность распределения непрерывной случайной величины Х в ин-

тервале

−

π

;

π

равна

p(x)=

2

cos

2

x ; вне этого интервала р(х) = 0. Найти ве-

2

2

π

роятность того, что в трех независимых испытаниях Х примет два раза значе-

0;

π

ние, заключенное в интервале

4

.

Ответ:

π

=

π +

2

;

P

(2)= C 2

π +

2 2

3π − 2

.

P 0 < X <

4π

4π

4π

4

3

3

8.14.

Функция

распределения

случайной

величины Х имеет вид

F(x) = a −b arctgx. Определить постоянные а,

b

и найти плотность распреде-

ления вероятностей р(х).

	Ответ: a =	1	;	b = −	1	; p(x) =	1	.
		2			π		π(1 + x2 )

Числовые характеристики непрерывных случайных величин

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

M (X )= +∞∫xp(x)dx,

−∞

где р(х) — плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения

принадлежат интервалу (a; b), то M (X )= ba∫xp(x)dx.

Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством

D(X )= +∞∫ [x − M (X )]2 p(x)dx,

−∞

если интеграл сходится, или равносильным равенством

D(X )= +∞∫ x2 p(x)dx −[M (X )]2.

−∞

В частности, если все возможные значения Х принадлежат интервалу

(a; b), то

90