Лекции по сопротивлению материалов II сем

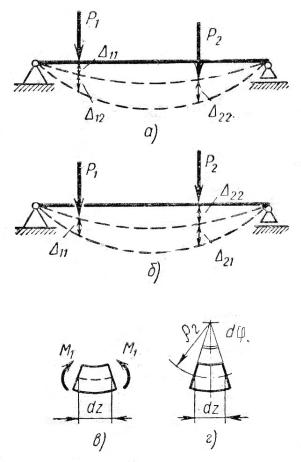
11

независимости действия сил и рассмотрим два сценария загружения.

В первом случае, приложим сначала к балке силу Р1, а затем к деформированной

балке силу Р2, рис. 12.2, а. Определим работу произведенную внешними силами. Сила Р1 на своем перемещении 11 произведет работу

А11 = 0,5 Р1 11.

Множитель 0,5 выражает статический способ приложения силы, т.е. ее возрастанию от нуля до конечной величины. Работа силы Р2 на перемещении 22 будет

А22 = 0,5 Р2 22.

Рис. 12.2. Загружение балки двумя силами:

а - первый вариант загружения; б - второй вариант загружения; в - к вычислению работы внутренних сил первого состояния; г - деформирование бесконечно малого участка балки

во втором состоянии

Далее, вследствие приложения силы Р2		сила Р1 произведет дополнительную работу
на перемещении	12
	А12 = Р1	12.
Множитель 0,5	в последнем выражении отсутствует, так как на дополнительном пе-

ремещении сила Р1 представлена своей полной величиной (на протяжении всего пере-

мещения она постоянна). Дополнительная работа, это работа произведенная силой

12

или системой сил на перемещениях вызванных действием другой силы или системы сил. Для дальнейшего изложения примем, что дополнительная работа может рассмат-

риваться не только как действительная, но и как возможная, т.е. произведенная воз-

можной нагрузкой. Поэтому дополнительную работу в таком случае называют воз-

можной или виртуальной работой.

Полная работа внешних сил при первом варианте загружения равна

А1 = А11 + А22 + А12.			(12.1)
Во втором варианте загружения, приложим сначала к балке силу Р2, а затем Р1,
рис. 12.1, б. Сила Р2 на своем перемещении		22 произведет работу
А22	= 0,5 Р2	22.
Работа силы Р1 на перемещении	11 будет
А11	= 0,5 Р1	11.
Дополнительная работа силы Р2 на перемещении			21, вызванном действием силы Р1

А21 = Р2 21.
Полная работа внешних сил при этом варианте загружения будет равна
А2 = А11 + А22 + А21.	(12.2)

Однако, из принципа независимости действия сил известно, что конечное состояние

системы не зависит от порядка ее нагружения и, следовательно, А2 = А1,
откуда получим
А21 = А12.	(12.3)
Или
Р1 12 = Р2 21.	(12.4)

Таким образом мы доказали теорему о взаимности работ которая гласит, что работа

внешних сил первого состояния на перемещениях второго состояния равна работе

внешних сил второго состояния на перемещениях первого состояния. Эта теорема называется теоремой Бетти по имени опубликовавшего ее итальянского ученого (Энри-

ко Бетти). Здесь эта теорема доказана на примере воздействия сосредоточенных нагру-

зок, однако она справедлива для любых видов нагрузки. Следует только помнить, что для сил перемещением является удлинение, а для моментов угол поворота. Из теоремы о взаимности работ следует, как частный случай теорема о взаимности перемещений

(теорема Максвелла). Принимая величины усилий равными единице, Р1 = Р2 = 1 из

(12.4) получим

13

δ12 = δ21,

(12.5)

где символ δ, вместо , означает перемещения, вызванные единичными силами.

Теорема Максвелла о взаимности перемещений формулируется следующим образом.

Перемещение точки приложения единичной силы по ее направлению, вызванное приложением второй единичной силы, равно перемещению точки приложения второй единичной силы по ее направлению вызванному первой единичной силой.

Подобно принципу взаимности работы внешних сил также доказывается и взаимность дополнительной работы внутренних сил (не будем здесь приводить это доказательство)

W12 = W21. (12.6)

Работа W12 это дополнительная работа внутренних сил в состоянии 1 на перемещениях вызванных силами состояния 2. В нашем случае, если мы рассмотрим бесконечно ма-

лый отрезок балки длиной dz, рис. 12.2 в,г, то работа внутренних сил на этом отрезке будет

dW12 = М1 dφ2 .

Из чертежа (рис. 12.2 г) видно, что

dφ2 = dz / ρ2.

Известно, однако, что

1 / ρ2 = M2 / (ЕJ),

и, следовательно

dW12 = М1 M2 dz / (ЕJ).

Чтобы вычислить дополнительную работу для всей балки необходимо проинтегриро-

вать последнее выражение по ее длине

W12 = ∫ М1 M2 dz/ (ЕJ),

(12.7)

ℓ

где М1 и M2 - текущие изгибающие моменты в первом и во втором состояниях.

Заметим далее, что согласно закону сохранения энергии работа внешних сил А12 долж-

на быть по абсолютной величине равна работе внутренних сил W12
А12 = W12 и аналогично	А21 = W21,
откуда следует
А12 = А21 = W12 = W21.		(12.8)

Последнее соотношение означает, что дополнительные работ двух состояний равны между собой.

Теперь мы получили все необходимые соотношения, для того, чтобы сформули-

ровать общий метод определения перемещений, пригодный для любой линейно дефор-

14

мируемой системы при любых воздействиях. Пусть, например, требуется определить вертикальное перемещение в точке А однопролетной балки, нагруженной произволь-

ной нагрузкой, рис. 12.3, а. Состояние балки под нагрузкой назовем действительным.

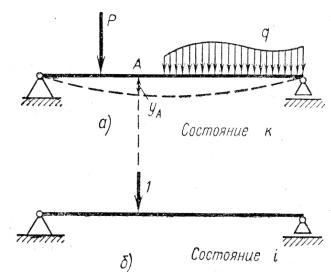
Рис. 12.3. К выводу формулы Мора:

а - действительное состояние системы; б - виртуальное состояние

Величины, относящиеся к действительному состоянию будем обозначать индексом «к».

Если еще раз внимательно проанализировать соотношение (12.8), то можно заметить,

что дополнительная работа второго состояния всегда осуществляется на перемещениях и деформациях первого состояния. Поэтому, если за первое состояние принять дейст-

вительное состояние, то второе состояние можно выбрать так, чтобы было удобнее вы-

числять искомые перемещения. Т.е. второе состояние может быть выбрано произволь-

но, оно может быть возможным или виртуальным. Виртуальное состояние выбираем следующим образом. На исходную балку, лишенную нагрузки, в точке А, точке опре-

деления искомого перемещения и по его направлению, прикладываем безразмерную силу величина которой равна единице - единичную силу, рис. 12.3, б. Это состояние мы будем обозначать индексом «i». Вычислим дополнительную работу внешних и внут-

ренних сил виртуального состояния на перемещениях действительного состояния.

Работа внешних сил будет равна произведению единичной силы на искомое пе-

ремещение	Аik = 1· уа = уа,
а дополнительная работа внутренних сил согласно (12.7)
	Wik = Wki = ∫Мk Mi dz / (ЕJ).
	ℓ
Но в силу (12.8) можно записать А21 = W12 и следовательно
	уа = ∫ Мk Mi dz / (ЕJ).	(12.9)

15

ℓ

Соотношение (12.9) и есть формула Мора (Отто Христиан Мор), которую он опублико-

вал в 1874 г. С помощью этой формулы определяются перемещения в любой точке ли-

нейно-деформируемой стержневой системы. Если необходимо определить угловое пе-

ремещение, то в качестве силы в виртуальном состоянии необходимо приложить без-

размерный единичный изгибающий момент. Произведение моментов в подынтеграль-

ном выражении должно выражаться аналитическими функциями и это выражение мо-

жет иметь кусочный характер как вследствие кусочного характера нагрузки, так и вследствие того, что конструкция может состоять из набора различных стержней. По-

этому следует использовать формулу для перемещений в более общем виде

=∑ ∫ Мk Mi dz / (ЕJ).

(12.10)

ℓ

В этой формуле знак суммирования распространяется на все части стержневой системы с аналитическим выражением для произведения изгибающих моментов. Заметим, что формула Мора имеет универсальный характер и если стержни системы подвержены воздействию только продольных усилий, то она имеет вид

=∑ Nk Ni ℓ /(ЕF). (12.11)

В заключение этой части отметим, что в случае вычисления прогибов при поперечном изгибе или при изгибе с растяжением (сжатием) обычно достаточно учитывать только изгибные усилия.

На практике вместо непосредственного вычисления интеграла Мора используют так называемый метод «перемножения эпюр» или способ Верещагина. Он был пред-

ложен в 1924 г. студентом Московского института инженеров транспорта (МИИТ)

Константином Андреевичем Верещагиным. Рассмотрим две эпюры изгибающих мо-

ментов, рис. 12.4. Верхняя эпюра относится к действительному состоянию, а нижняя к виртуальному состоянию части стержневой системы. Жесткость стержня ЕJ на участке АВ будем считать постоянной и в соотношении (12.9) вынесем ее за знак интеграла

B B

∫ Мk Mi dz / (ЕJ) = (1/ (ЕJ)) ∫ Мk Mi dz.

A A

Величина Mк dz представляет собой элементарную площадь dωк эпюры изгибающих моментов действительного состояния, см. рис. 12.4, следовательно

B В

∫ Мk Mi dz = ∫ Mi dωк.

A А

Здесь и далее все величины будем вычислять с точностью до множителя 1/ (ЕJ).

16

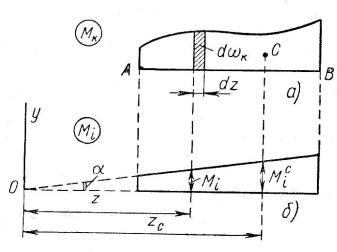
Рис. 12.4. К доказательству метода перемножению эпюр по Верещагину

Но Mi = z tg α, следовательно

B В

∫ Mi dωк = tg α ∫ z dωк.

A А

Заметим, что последнее интегральное выражение представляет собой ничто иное, как статический момент эпюры изгибающих моментов Мk относительно некоторой оси у, проходящей через точку О В

Sо = ∫ z dωк.

А

С другой стороны, статический момент равен произведению площади на расстояние от центра тяжести до оси и равен zс· ωк. Из чертежа на рис. (12,4) следует, что

zс = Mсi /tg α,

где Mсi - ордината эпюры моментов Mi, расположенная под центром тяжести эпюры Мk

и поэтому окончательно можно записать

B	В	B
∫Мk Mi dz = ∫ Mi dωк = tg α ∫ z dωк = tg α zс ωк = ωк Mсi .			(12.12)
A	А	A

Таким образом, интеграл Мора равен произведению площади действительной эпюры моментов на расположенную под ее центром тяжести ординату эпюры виртуальных моментов. Действительная эпюра моментов Мk может быть криволинейной, а эпюра виртуальных моментов Mi - только прямолинейной. Если величина ωк Mсi положи-

тельна это означает, что вычисленное перемещение совпадает с направлением единич-

ной силы.

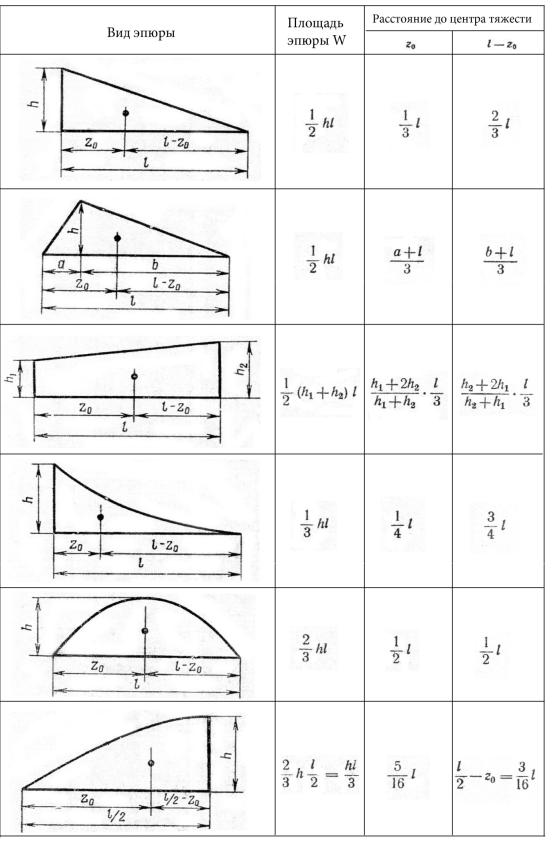
В таблице 12.1 приведены часто встречающиеся эпюры и их характеристики, а в таблице 12.2 результаты перемножения двух криволинейных эпюр на прямолинейные

17

по методу Верещагина.

Площади и координаты центра тяжести простейших эпюр. Таблица 12.1.

18

Результаты перемножения эпюр при вычислении интеграла Мора. Таблица 12.2.

На практике для перемножения прямолинейных эпюр наиболее удобно использо-

вать формулу перемножения трапеций, рис. 12.5. Эта формула универсальна, так как любой треугольник или прямоугольник является вырожденной трапецией.

∫Мk Mi dz =		(2ac + 2bd+ ad + bc).	(12.13)

ℓ

При применении этой формулы необходимо учитывать знаки ординат эпюр: если они однозначные, перед слагаемыми в формуле 12.13 ставится знак плюс, если разнознач-

ные, то принимается знак минус.

Рис. 12.5. К перемножению эпюр в виде двух трапеций по Верещагину

Рассмотрим пример вычисления перемещений. Требуется определить вертикаль-

ное перемещение точки В, конца консоли, изображенной на рис. 12.6 a. Изгибная жест-

кость консольной балки постоянна по ее длине. Для определения перемещения точки В приложим в этой точке единичную силу и построим единичную эпюру моментов. Для вычисления перемещения необходимо вычислить интеграл Мора по методу Верещаги-

на, т.е. перемножить эпюры моментов Мр и М1. Для этого, воспользуемся принципом

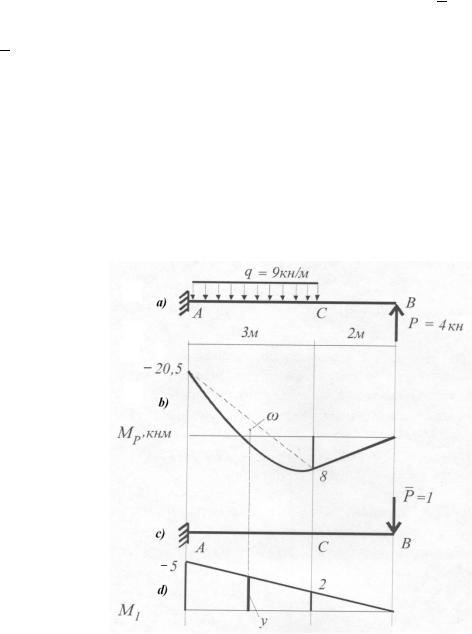
19

независимости действия сил и криволинейный участок эпюры моментов Мр представим как сумму двух геометрических фигур – трапеции и параболы. Трапеция имеет основа-

ни равное 3 метрам, со сторонами - 20,5 кнм и 8 кнм. Парабола имеет максимальную

ординату qℓ2/8= 9 · 32/8 = 10,125 кнм. Площадь параболы ώ = (qℓ2/8)·3 =

= · 10,125 · 3 = 20,25. Здесь ℓ = 3 м проекция основания параболы на горизонталь-

ную ось. Ордината единичной эпюры, находящаяся под центром тяжести параболы оп-

ределится из подобия треугольников y= (-5/5) · 3,5 = - 3,5 кнм. Таким образом, верти-

кальное перемещение точки В будет: ЕJ υВ = ∫Мр M1 dz или по правилу Верещагина

υВ =		(2 · 20,5 · 5 – 2 · 8 · 2 + 2 · 20,5 – 8 · 5 ) – 20,25 · 3,5 -		(-2 · 8 · 2) =5,458(3)ЕJ	м.

Рис. 12.6. К вычислению перемещений конца консоли

a– схемабалки и нагрузок; b– эпюраизгибающих моментов в действительномсостоянии; c– схемаприложения единичной силы;d– эпюраизгибающих моментов от единичной силы

Лекция 13

20

Простейшие статически неопределимые балки и стержни. Степень статической неопределимости, определение «лишних» связей. Выбор основной системы. Уравнения совместности деформаций.

Представленный ранее аппарат для вычисления перемещений в виде интеграла Мора и метода единичных нагрузок можно очень удачно применить для расчета ста-

тически неопределимых систем: рам и балок. Здесь мы рассмотрим методы расчета только простейших статически неопределимых балок.

Как уже известно, балки крепятся на опорах при помощи элементарных связей, а

опорные реакции в этих связях определяются с помощью уравнений равновесия. Так как, для балки можно составить только три уравнения равновесия, с их помощью мож-

но определить реакции только в трех элементарных связях. Балки, которые закреплены к основанию тремя элементарными связями являются статически определимыми.

С другой стороны число связей для балки не может быть меньше трех, так как в этом случае балка превращается в механизм (геометрически изменяемую систему), она по-

лучает возможность перемещаться без деформаций. Однако, в строительной практике применяются балки в которых число элементарных связей в опорах может быть более трех. Балки, а в общем случае и другие плоские системы, в которых число связей пре-

вышает число уравнений равновесия называются статически неопределимыми. Связи,

количество которых превышает число связей в статически определимых системах,

называют условно лишними связями, а усилия в них лишними неизвестными. Число лишних неизвестных определяет степень статической неопределимости системы, на-

пример: один раз статически неопределимая, трижды статически неопределимая и т.д.

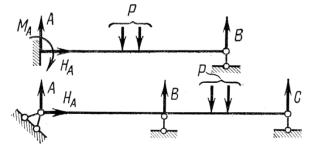
На рис. 13.1 представлены две один раз статически неопределимые балки, так как у ка-

ждой из них имеются по четыре опорных элементарных связи.

Рис. 13.1 Две статически неопределимые балки Для того, чтобы сформулировать общий подход к расчету статически неопреде-

лимых балок, рассмотрим пример расчета балки с одной лишней связью, рис. 13.2. На рисунке представлена консоль, левый конец которой, точка А, жестко защемлен (три