Лекции по сопротивлению материалов II сем

31

телен, см. рис. 11.2. Поскольку стержень закреплен симметрично, максимальное гори-

зонтальное перемещение f будет в его середине,	при z = ℓ/2. Предположим, что изо-
гнутая ось стержня (упругая линия) имеет форму синусоиды вида:
y = f sin (π z/ℓ).	(14.3)

На концах стержня при z = 0 и при z = ℓ, y = 0. В середине стержня z = ℓ/2,

y = f sin (π 0,5ℓ/ℓ) = f sin (π/2) = f,

т.е. при принятой аппроксимации упругой линии граничные условия выполняются.

Подставив выражение для горизонтального перемещения (14.3) в выражение для изги-

бающего момента (14.2); получим:

MZ = - PK f sin (π z/ℓ).

Теперь подставим выражение для изгибающего момента в дифференциальное уравне-

ние упругой линии (11.5) Е J d2y /dz2 = M,

Е J d2y /dz2 = - PK f sin (π z/ℓ).

Для решения этого уравнения проинтегрируем его два раза:

ЕJ dy /dz= PK f cos (π z/ℓ) + C1,

ЕJ y = PK f ℓ2/ (π2) ( sin (π z/ℓ) + C1 z + C2.

Найдем постоянные интегрирования. В середине стержня при z = ℓ/2 первая произ-

водная dy /dz= 0 и С1 = 0, так как cos (π/2) = 0. При z = 0, y =0 и из второго уравне-

ния следует, что С2 = 0 . Следовательно, уравнение упругой линии можно представить в виде

ЕJ y = PK f ℓ2/ (π2) ( sin (π z/ℓ),

атак как при z = ℓ/2, y = f, то можно записать

Е J f = PK f ℓ2/ (π2) ( sin (π/2) или Е J f =	PK f ℓ2/ π2,
откуда получим
PK = π2 Е J / ℓ2 .	(14.4)

Выражение (14.4) и есть формула Эйлера для стержня шарнирно закрепленного по концам. Будем считать этот случай основным. Для других способов закрепления эта формула несколько изменится. Рассмотрим несколько характерных случаев закрепле-

ния стержней.

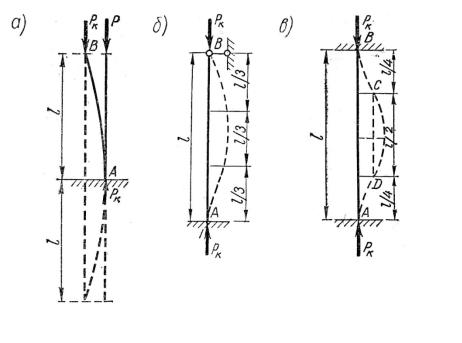
Пусть стержень жестко закреплен в основании, а в верхнем конце свободен, рис. 14.4 а. Сжимающая нагрузка приложена к свободному концу. Предположим, что эта сила достигла критического значения и стержень сохраняет устойчивость при незначи-

32

тельном отклонении от линии АВ. Из сравнения этого случая с основным видно, что изогнутая ось стержня находится в тех же условиях, что и у шарнирно закрепленного стержня, только на длине вдвое большей. Следовательно, критическая сила для стерж-

ня длиной ℓ, защемленного одним концом в основании, будет той же, что и для стерж-

ня с шарнирно закрепленными концами длиной 2ℓ. Следовательно, для этого случая формула Эйлера для вычисления критической силы примет вид

PK = π2Е J/(2ℓ)2.

(14.5)

Рис. 14.4. К определению расчетной длины стержней Другим случаем характерного закрепления является закрепление, когда основание

стержня закреплено жестко, а верхний конец, к которому приложена сжимающая сила,

закреплен шарнирно, рис. 14.4 б. В этом случае можно заметить, что перегиб изогнутой оси стержня находится приметно на расстоянии 1/3ℓ от нижнего конца стержня. Изги-

бающий момент в точке перегиба равен нулю, поэтому напряженное состояние в этом сечении можно отождествить с шарниром. Значит, верхние 2/3 длины стержня нахо-

дятся в таком же напряженном состоянии, как и шарнирный стержень, длиной 2/3ℓ.

Поэтому выражение для критической силы в этом случае можно представить в сле-

дующем виде:

PK ≈ Е J π2/(0,7ℓ)2.

(14.6)

Следующим типом закрепления служит стержень, жестко защемленный с двух концов, рис. 14.4 в. Рассмотрение упругой линии стержня в этом случае показывает,

что стержень имеет две точки перегиба на расстоянии 1/4ℓ от точек закрепления и его

33

средняя часть деформируется также как шарнирно закрепленный стержень длиной ℓ/2.

Выражение для вычисления критической силы в этом случае будет:

PK = π2Е J/(0,5ℓ)2 .

(14.7)

Все вышеприведенные формулы (15.4) - (15.7) можно свести в одну введя вместо

числовых коэффициентов при длине буквенный коэффициент:

PK = π2Е J /(μℓ)2 ,

(14.8)

где μ - коэффициент приведенной длины, зависящий от способа закрепления стержня.

Величина μℓ = ℓ0 называется приведенной или свободной длиной стержня и может быть истолкована как длина некого шарнирного стержня, имеющего такую же критиче-

скую силу, как и заданный стержень.

В некоторых, важных для проверки устойчивости стержней случаях, необходимо оперировать критическими напряжениями в стержнях, т.е. напряжениями которые воз-

никают при действии критической силы. Вычислим это критическое напряжение:

σК = PK/F = π2 Е J /(ℓ02 F),

где: F - площадь поперечного сечения стержня; J - момент инерции его сечения.

Из курса сопротивления материалов известно также, что J = F i2. Величина i является некоей линейной характеристикой поперечного сечения, его параметром и называется радиусом инерции. Подставив выражение для момента инерции через площадь и ради-

ус инерции в выражение для критического напряжения, получим

σК = π2 Е /(ℓ0/i)2.

(14.9)

Величина, стоящая в знаменателе этого выражения - отношение свободной длины к ра-

диусу инерции стержня называется гибкостью стержня и обозначается буквой λ

λ = ℓ0/i = μℓ/ i.

(14.10)

Отметим, что в данном случае точное математическое выражение для гибкости совпа-

дает с бытовым его понятием. Действительно, чем больше отношение длины стержня к характерному размеру его поперечного сечения, тем больше гибкость. Подставив вы-

ражение для гибкости в (15.9) получим окончательно

σК = π2 Е / λ2.

(14.11)

Из последнего выражения следует, что критическое напряжение прямо пропорцио-

нально модулю упругости и обратно пропорционально квадрату гибкости стержня.

34

Лекция 15.

Пределы применимости формулы Эйлера. Проверка устойчивости стержней. Подбор сечений стержней по устойчивости.

Формула (14.11) для критического напряжения σК= π2 Е / λ 2 позволяет опреде-

лить пределы применимости формулы Эйлера.Эта формула с момента своего опубли-

кования непрерывно подвергалась критике. Результаты опыта и экспериментов не все-

гда подтверждали ее корректность. Дело здесь в том, что формула Эйлера выведена в предположении, что материал деформируется упруго и линейно, и что напряжения сжатия в стержне не превышают предела пропорциональности σпц. Поэтому, если

σК ≤ σпц, формула Эйлера применима, в противном случае она некорректна. Границей

применимости формулы служит случай σК = σпц. Заменим в формуле (14.11) σК на

σпц и вычислим из нее соответствующую граничную гибкость λпр

λпр =	( π2 Е / σпц)0,5.	(15.1)
Для строительной стали σпц ≈ 2000	кгс/см2, Е = 2100000 кгс/см2	и

λпр = ( 3.14.1592 · 2100000 / 2000)0,5 ≈ 100,

т.е., если гибкость стержня λ ≥ 100, формула Эйлера применима, если λ < 100, то нет.

Другими словами формула Эйлера применима только для тонких и длинных стержней,

стержней с большой гибкостью. Эксперименты показывают, что если критическое на-

пряжение оказывается больше предела пропорциональности, то действительная крити-

ческая сила, полученная в опыте, получается гораздо меньше критической силы, вы-

численной по формуле Эйлера. Теоретическое определение критической силы, в случае работы материала за пределом пропорциональности и упругости является сложной за-

дачей и поэтому исследователи получили эту зависимость экспериментальным путем.

На основе опытных данных Ф. С. Ясинским была предложена эмпирическая формула для определения критического напряжения в сечениях стержней для ряда конструкци-

онных материалов: σК = α - b λ, (15.2)

где α и b - эмпирические коэффициенты, зависящие от вида материала.

Так, например, для мягкой строительной стали

σК = 3100 - 11,4 λ, кгс/см2,

для древесины

σК = 293 - 1,94 λ кгс/см2.

35

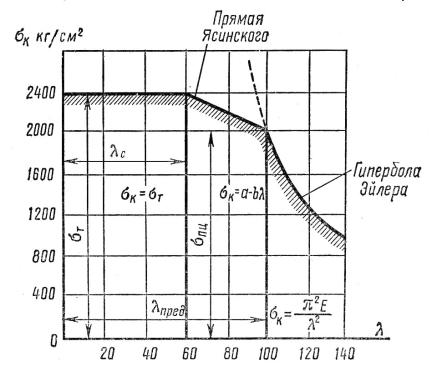
Формула Ф. С. Ясинского также непригодна для всего диапазона λ < λпр гибкости стержней. На рис. 15.1 приведен график зависимости критического напряжения от гиб-

кости для строительной стали. Для гибкостей λ в диапазоне 0 ≤ λ ≤ λс (для стали

λс = 60, рис. 15.1) критическое напряжение постоянно σК = σТ. Другими словами, для коротких стержней критическим напряжением является расчетное сопротивление стали

Рис. 15.1. Зависимость критического напряжения от гибкости для строительной стали

сжатию. Такие стержни разрушаются не от потери устойчивости, а от потери прочно-

сти. В пределах λс ≤ λ ≤ λпр справедлива формула Ф. С. Ясинского, а при гибкостях

λ > λпр формула Эйлера. Определив величину критического напряжения,	можно вы-
числить значение критической силы по формуле
PK = σК F.	(15.3)

Выясним теперь, как следует производить проверку стержней на устойчивость при продольном изгибе. При проверке прочности на сжатие сравниваются действующие в сечении напряжения σс с расчетным сопротивлением Rрас

σс = P / F ≤ Rрас ,

(15.4)

где: P - усилие сжатия; F - площадь поперечного сечения стержня.

Очевидно, что и при проверке на устойчивость необходимо сравнить критические на-

пряжения с гипотетическим расчетным сопротивлением продольному изгибу - RК:

	36
σ = N / F ≤ σК = PK / F = RК.	(15.5)

Для выяснения характера этого сопротивления разделим критическое напряжение σК

на напряжение сжатия, когда соотношения (15.4) и (15.5) превращаются в равенства:

σК / σс = RК / Rрас, откуда получим: σК = (RК / Rрас) σс = (σК / Rрас) σс = φ σс, или

окончательно:

σК = φ σс = φ Rрас .
Коэффициент φ называется коэффициентом продольного изгиба,
φ = σК / Rрас.	(15.6)

Таким образом, коэффициент продольного изгиба равен отношению критического на-

пряжения к расчетному сопротивлению материала на сжатие и является функцией гиб-

кости стержня. Каждому участку диаграммы критического напряжения, рис. 15.1, соот-

ветствует свой способ вычисления коэффициента продольного изгиба. На первом уча-

стке, 0 ≤ λ ≤ λс.

φ = 1;

на втором участке, при λс ≤ λ ≤ λпр, коэффициент φ вычисляется с помощью форму-

лы Ясинского (15.2)
φ = (α - b λ) / Rрас;	(15.7)
а на третьем участке при λ > λпр, по формуле Эйлера (14.11)
φ = π2 Е /( λ2 Rрас).	(15.8)

С учетом коэффициента продольного изгиба, условие проверки прочности при про-

дольном изгибе можно переписать в виде

N ≤ φ Fбр Rрас,

(15.9)

где: N - усилие, действующее на стержень; Fбр - площадь поперечного сечения брутто.

При данной проверке, берется площадь поперечного сечения без учета ослаблений.

Многочисленными экспериментами установлено, что местное ослабление сечений не влияет на устойчивость стержней. Коэффициент продольного изгиба φ всегда меньше или равен единице и его физический смысл состоит в том, что он как бы уменьшает расчетное сопротивление материала или площадь поперечного сечения стержня при гибкостях, когда необходимо учитывать влияние продольного изгиба. Для некоторых материалов значения коэффициента продольного изгиба, в зависимости от гибкости,

приводятся в таблицах, для других материалов в строительных нормах приводятся кон-

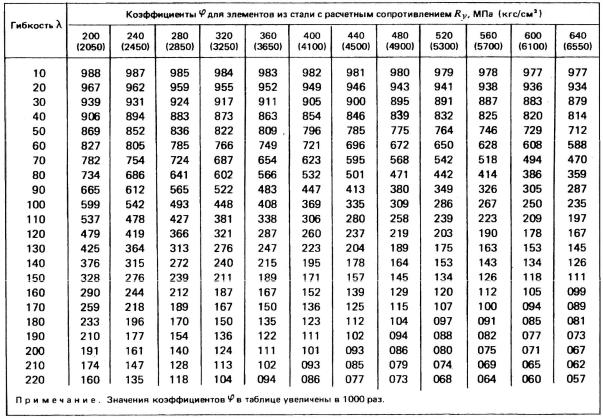
кретные формулы для вычисления коэффициента продольного изгиба. Значение коэф-

37

фициента продольного изгиба для сталей различной прочности приведено в табл. 15.1.

Для деловой древесины коэффициент φ вычисляется следующим образом. Предельная

гибкость для дерева λпр = 70. При λ < 70 (через формулу Ясинского)
φ = 1 - 0,8 (λ / 100)2 ,	(15.10)
при λ > 70 (через формулу Эйлера)
φ = 3000 / λ2.	(15.11)

Коэффициенты φ продольного изгиба центрально-сжатых элементов. ТАБЛИЦА 15.1

Обобщая полученные результаты можно сказать, что нами получен аппарат бла-

годаря которому можно решать как задачи поверочного расчета: определение критиче-

ской нагрузки и проверку устойчивости центрально сжатых элементов конструкций,

так и задачи прямого проектирования: определение необходимых размеров сечений по заданным нагрузке, длине и характеристикам материла. Рассмотрим несколько приме-

ров.

Пример 15.1. Определить критическую нагрузку для деревянной стойки, длиной 4 м,

закрепленной шарнирно по концам. Размеры поперечного сечения 12 х 18 см. Модуль упругости древесины Е = 90000 кгс/см2.

Решение. Площадь сечения стойки

F = 12 х 18 = 216 см2.

38

Наименьший момент инерции

J = h b3/ 12 = 18 · 123/ 12 = 2592 см4. Соответствующий радиус инерции

i = (J / F)0,5 = (2592 / 216)0,5 = 3,47 см. Определяем гибкость стойки по соотношению (14.10)

λ = μℓ/ i = 1 · 400 / 3.47 = 115,27 > λпр = 70, следовательно, критическую силу необходимо определять по формуле (14.8) Эйлера;

PK = π2Е J /(μℓ)2 = 9,87 · 90000 · 2592 / 4002 = 14390 кгс.

Пример 15.2. Определить величину допустимой нагрузки на деревянную стойку высотой ℓ = 5 м, сечением 18 х 22 см. Концы стойки закреплены шарнирно. Расчетное сопротивление древесины с учетом коэффициентов условий работы RС = 100 кгс/см2.

Решение. Площадь сечения стойки

F = 22 х 18 = 396 см2. Наименьший момент инерции

J = h b3/ 12 = 22 · 183/ 12 = 10692 см4,

радиус инерции

i = (J / F)0,5 = (10692 / 396)0,5 = 5,18 см.

Гибкость стойки

λ = μℓ/ i = 1 · 500 / 5,18 = 96,7 > λпр = 70,

следовательно, коэффициент продольного изгиба определятся по соотношению (15.11)

φ = 3000 / λ2 = 3000 / 96,72 = 0,32.

Допустимую нагрузку определим по соотношению (15.9)

N ≤ φ Fбр Rрас = 0,32 · 396 · 100 = 12672 кгс.

Пример 15.3. Определить допустимую нагрузку и критическую силу для стойки из

стального прокатного двутавра № 30, длиной 5 м, защемленного в основании и шар-

нирно закрепленного в верхнем конце. Модуль упругости стали Е = 2100000 кгс/см2, расчетное сопротивление R = 2850 кгс/см2.

Решение. Из сортамента прокатных изделий для двутавра № 30 определяем необходимые данные: площадь поперечного сечения F = 46,5 см2, наименьший момент инерции

J = 337 см4, радиус инерции i = 2,99 см. Определяем гибкость стойки в плоскости
y	y
наибольшей гибкости
	λ = μℓ/i = 0,7 · 500 / 2,99 = 117 > λпр = 60.
По гибкости	λ и расчетному сопротивлению R из таблицы 15.1 получаем значение

39

коэффициента продольного изгиба, используя интерполяцию, φ = 0,384. Определяем допустимую нагрузку

N ≤ φ Fбр Rрас = 0,384 · 46,5 · 2850 = 50890 кгс. Теперь подсчитаем критическую силу по соотношению (14.8)

PK = π2Е J /(μℓ)2 = 9,87 · 2100000 337 / 3502 = 57020 кгс.

N = 50890 < PK = 57020,

следовательно, задача решена - допустимая нагрузка на стойку N = 50890 кгс.

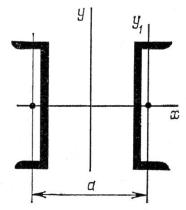
Пример 15.4. Решим задачу прямого проектирования. Требуется подобрать сечение колонны с поперечным сечением из двух швеллеров, рис. 15.2. Высота колонны 6,0 м, расчетное сопротивление стали R = 2450 кгс/см2. Нагрузка на колонну Р = 90,0 тс.

Концы колонны жестко защемлены при изгибе относительно вещественной оси Х и шарнирно закреплены в ортогональном направлении: μх = 0,5; μу= 0,7.

Решение. Будем искать такую геометрию сечения, чтобы обеспечить равноустойчивость колонны относительно осей X и Y.

Рис. 15.2. Поперечное сечение составной колонны.

Сначала подберем сечение исходя из возможносит потери устойчивости в плоскости YOZ, т.е. при изгибе вогруг оси Х. Подбирать сечение колонны, будем исходя из соотношения (15.9)

Fтр = N / φ R.

Это соотношение содержит два связанных между собой неизвестных Fтр и φ, поэтому воспользуемся методом последовательных приближений. Зададимся начальным значением φ = 0,5 и вычислим требуемую площадь поперечного сечения колонны

Fтр = N / (φ R) = 90000 / (0,5·2450) = 73,47 см2.

Так как колонна состоит из двух швеллеров, ищем по сортаменту подходящий швеллер с площадью поперечного сечения Fшв = 73,47 / 2 ≈ 37 см2. Принимаем швеллер № 24 с характеристиками: F= 30,6 см2, Jх = 2400 см4, радиус инерции iх =9,7 см. Jу1= 208 см4,

40

радиус инерции iу1 = 2,6см. Вычислим гибкость сечения в плоскости YOZ:

λ = μх ℓ/iх = 0,5 · 600 / 9,7 = 30,92.

По таблице 15.1 находим φ = 0,927, что существенно отличается от начального значения φ = 0,5. Примем полусумму полученных величин и повторим попытку

φ = 0,5(0,5 + 0,927) ≈ 0,714.

Fтр = N / φ R = 90000 / (0,714·2450) = 51,45 см2, Fшв = 50,66 /2 = 25,72 см2.

По сортаменту находим швеллер № 18 : F = 20,7 см2, Jх = 1090 см4, радиус инерции iх =7,24 см. Jу1= 86 см4, радиус инерции iу1 = 2,04 см. Вычислим гибкость сечения относительно оси Х:

λх = μх ℓ/iх = 0,5 · 600 / 7,24 = 41,4.

По таблице 15.1 находим φ = 0,888. Проверим прочность колонны с подобранным сечением

N = 90000 ≤ φ Fбр Rрас = 0,888 · 2 · 20,7 · 2450 = 90698 кгс.

Запас прочности 100 · (90698 - 90000) / 90000 = 0,775 %. Окончательно принимаем колонну из двух швеллеров № 18, F = 2· Fшв = 41,4 см2.

Подберем теперь расстояние α между ветвями колонны, рис. 15.2 из условия равноустойчивости. Из соотношения (14.9) видно, что одинаковая устойчивость относительно осей Х и Y, будет обеспечена при равенстве гибкостей λх = λу.

Запишем выражение для гибкости относительно оси Y в (плоскости XOZ): λу = μу ℓ/ iу = μу ℓ/ (Jу/ F)0,5 = λх = 41,4.

Из этого выражения можно вычислить требуемую величину момента инерции сечения относительно оси Y

Jу = F (μу ℓ/ λх)2 = 41,4 · (0,7 · 600 / 41,4)2 = 4260 см4.

С другой стороны

Jу = 2 [Jу1 + Fшв (0,5 α)2],

откуда

α = 2 [(0,5 Jу - Jу1) / Fшв]0,5 = 2 [(0,5·4260 - 86) / 20,7]0,5 = 19,87 см.

Задача решена.