Лекции по сопротивлению материалов II сем

41

Лекция 16.

Сложное сопротивление. Косой изгиб. Расчет балок при косом изгиб. Понятие о нулевой линии. Вычисление прогибов при косом изгибе.

Ранее рассматривались такие виды деформирования конструкций, когда под действием внешних воздействий в них возникали простейшие виды напряженного со-

стояния: растяжение, сжатие или плоский изгиб. За рамками данного курса остались такие деформации как сдвиг и кручение. В действительности, элементы конструкций часто претерпевают не одну простую деформацию, а их комбинации. Например, колон-

ны, нагруженные эксцентрично, испытывают не только сжатие, но и изгиб, в стержнях ферм и рам возможна комбинация растяжения с изгибом, в валах машин возникает из-

гиб с кручением, возможны и более сложные комбинации деформаций. Такое дефор-

мирование элементов конструкций определяется как сложное сопротивление. При рас-

смотрении сложного сопротивления необходимо воспользоваться принципом незави-

симости действия сил, т.е. рассматривать отдельно напряженно деформированное со-

стояние от действия каждого простого нагружения, а затем складывать эти результаты для выявления наиболее опасного состояния конструкции с точки зрения прочности и перемещений.

Одним из видов сложного напряженного состояния является косой изгиб. Ранее,

при изучении плоского изгиба, предполагалось, что внешние силы лежат в одной плос-

кости с главной осью инерции сечения, т.е. в главной плоскости. В этом случае в этой же плоскости происходят и поперечные перемещения точек оси балки. На практике,

встречаются случаи, когда плоскость действующих на балку усилий проходит через ее ось, но она не совпадает с главной плоскостью. В этом случае балка будет деформиро-

ваться не в плоскости действия сил, и этот случай называется плоским косым изгибом.

Возможен другой случай, когда силы, действующие на балку по ее длине, действуют в разных плоскостях, и в этом случае деформированная ось балки вообще не лежит в од-

ной плоскости. Этот случай деформирования называется пространственным косым изгибом. Рассмотрим случай плоского косого изгиба. Такое напряженное состояние возникает, например, в обрешетинах кровли, рис. 16.1 а. Вертикальная нагрузка от веса кровли и нагрузка от снега, направлены по вертикали, т.е. под углом α к главной оси.

Другим примером косого изгиба может служить консоль из стального прокатного угол-

ка, находящаяся под действием собственного веса и вертикальной нагрузки, рис. 16.1 б.

В этом случае главная ось поперечного сечения консоли также наклонена к вертикали.

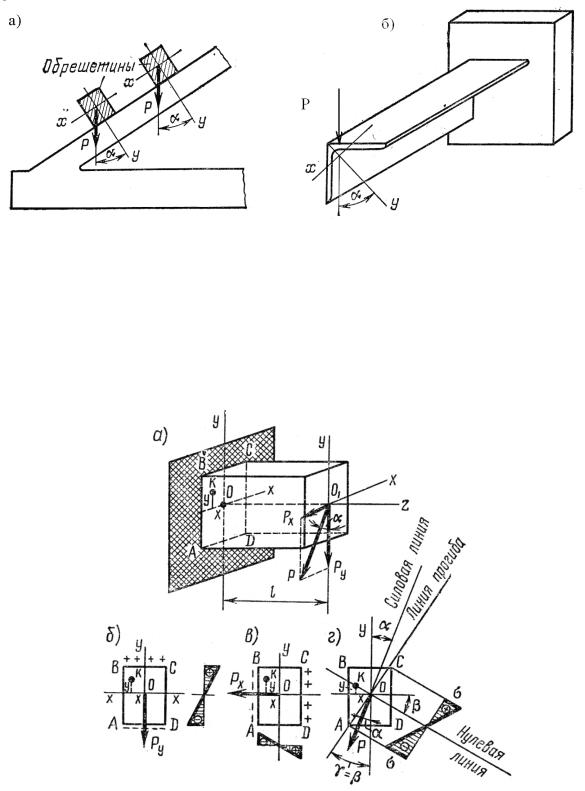
Рассмотрим деформацию косого изгиба на примере изгиба консоли прямоугольного сечения, находящейся под действием сосредоточенной силы Р, рис. 16.2.

42

Рис. 16.1. Примеры сложного сопротивления в виде косого изгиба:

а - обрешетины кровли; б - консоль из стального уголка Пусть на консоль действует сосредоточенная сила Р, приложенная к ее торцу в плоско-

сти, наклоненной к главной плоскости yoz под углом α, рис. 16.2 а .Требуется опреде-

лить напряжения в сечениях бруса. прогибы, а также положение нейтральной оси (ну-

левой линии) и построить эпюру нормальных напряжений в сечении бруса. Разложим

Рис. 16.2 Напряженное состояние сечения консоли при косом изгибе.

силу Р на две составляющие РХ и Py, действующие по направлению главных осей инерции сечения Ox и Oy. Эти составляющие равны:

РХ = P sin α; Py= P cos α.

Разложение действующей силы на две составляющие привело к тому, что мы можем рассматривать внутренние усилия консоли от действия силы Р как сумму от действия

43

двух плоских изгибов в направлении главных осей инерции. В приведенном примере самым напряженным сечением является сечение ABCD в заделке. Изгибающие момен-

ты в этом сечении будут:

МХ = Py · ℓ= P · ℓcos α; Мy = РХ · ℓ= P · ℓ sin α.

(16.1)

Момент МХ изгибает брус в плоскости главной оси инерции Y и нейтральной осью сечения ABCD будет ось Х. От действия этого момента, верхние волокна бруса бу-

дут растянуты, нижние сжаты, рис. 16.2 б. Момент Мy изгибает брус в плоскости главной оси инерции Х, а нейтральной осью будет ось Y. От действия этого момента,

правые волокна бруса будут растянуты, а левые сжаты, рис. 16.2 в. Для того, чтобы вычислить напряжения в произвольной точке К сечения, необходимо просуммировать напряжения вызываемые действием этих двух изгибающих моментов МХ и Мy:

σк = МХ · y / JХ + Мy · х / Jy,

(16.2)

где: х и у - координаты точки К; JХ и Jy - моменты инерции поперечного сечения от-

носительно осей Х и У.

Для угловых точек модули координат приобретают максимальное значение, поэтому формулу (16.2) для вычисления напряжений в них можно преобразовать к виду

σmax,min = ± MХ / WХ ± My / Wy.

Здесь WХ и Wy - моменты сопротивления сечения. Выбор знаков в этом соотноше-

нии зависит от того, растягивается ли волокно в рассматриваемой точке, или сжима-

ется. При растяжении принимается знак плюс, при сжатии - минус. При заданных на рис. 16.2 а услолвиях максимальные растягивающие напряжения будут в точке С, а

максимальные сжимающие в точке А

σС = MХ / WХ +My / Wy; σА = - MХ / WХ - My / Wy.	(16.3)
Напряжения в точках В и D будут
σВ = MХ / WХ - My / Wy; σD = - MХ / WХ + My / Wy.	(16.4)

Вычислив напряжения в угловых точках можно поострить эпюру напряжений по кон-

туру сечения или пространственную эпюру по всему сечению. Из рассмотрения эпюр на рис. 16.2 б, в, ясно, что нейтральная линия при косом изгибе не может совпадать с ни с одной из осей симметрии сечения, она должна проходить с наклоном к этим осям.

Для того, чтобы определить положение нулевой линии необходимо приравнять нулю нормальные напряжения в сечении, следовательно, используя соотношение (16.2)

можно записать:

	44
σ = МХ · yN / JХ + Мy · хN / Jy = 0,	(16.5)

где хN, yN - текущие координаты нулевой линии.

Анализ этого соотношения показывает, что его левая часть может быть равна нулю только тогда, когда его слагаемые имеют разные знаки. При этих условиях из (16.5)

получим	yN = [Мy JХ/ (МХ Jy)] хN,
и учитывая соотношения (16.1)
	yN = (JХ/ Jy) tg α хN.	(16.6)

Таким образом, нулевая линия это прямая проходящая через начало координат с угло-

вым коэффициентом tg β равным

tg β = (JХ/ Jy) tg α.	(16.7)
Угол β - это угол наклона нулевой лини к оси X,	отсчитываемый в первом положи-

тельном квадранте от оси абсцисс к оси ординат. Из соотношения (16.7) видно, что на-

правление нулевой линии, т.е. линии нулевых напряжений, не будет перпендикулярно силовой плоскости, наклоненной к оси ординат под углом α, как это бывает при плос-

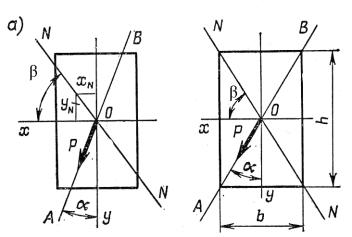
ком изгибе, рис. 16.3 а. Равенство этих углов обеспечивается только тогда, когда равны друг другу главные моменты инерции JХ = Jy, а это возможно только в симметричных сечениях, таких как круг, квадрат, правильные многоугольники и т.п. Интересно, что для прямоугольного бруса, когда силовая линия проходит по диагонали сечения, нуле-

вая линия проходит через другую диагональ, рис. 16.3 б. Действительно, если

Рис. 16.3. Нулевая линия в прямоугольном сечении:

линия А В - след силовой плоскости; линия N N - нулевая линия

силовая линия АВ проходит через диагональ прямоугольника tg α = b/h, из соотноше-

ния (16.7) получим:

tg β = (b/ h) (b h3/12) / (b3 h/12) = h/b.

45

Построив нулевую линию, можно из самых разнесенных точек сечения, провести линии параллельные ей (рис. 16.2 г) и построить эпюру нормальных напряжений по направлению перпендикулярному нулевой линии. Краевые ординаты этой эпюры будут соответствовать значениям максимальных напряжений в сечении. Умение находить точки с максимальными по модулю напряжениями при косом изгибе необходимо для проверки прочности сечений. Если сечение составлено из фигур с прямолинейными гранями, то наиболее опасную точку (точку с наибольшими по модулю напряжениями)

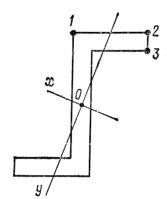
можно определить методом перебора. Например, на рис.16.4 изображен стержень с Z -

образным сечением. Для такого стержня достаточно вычислить напряжения в точках

1,2, и 3 и затем выбрать из полученных значений максимальное. В данном случае

Рис. 16.4.

максимальные напряжения имеют место в точке 2. Если же сечение имеет сложную не-

регулярную форму, то умозрительно найти наиболее опасную точку можно только по-

строив нулевую линию.

Вычисление прогибов балок при косом изгибе производится также на основе принципа независимости действия сил. Отдельно вычисляются перемещения оси балки от компонент усилий действующих в плоскости одной и другой главных осей. Затем эти перемещения складываются геометрически. Для рассмотренной консоли, рис.16.2 а,

найдем перемещение ее конца при действии силы Р. Вычислим перемещения υy от

действия силы Py и υх от действия силы РХ по направлению соответствующих осей.

υy = Py ℓ3/ (3 Е JХ); υХ = PХℓ3/ (3 Е Jy).
Полное перемещение вычисляется как геометрическая сумма составляющих
υ= (υ2y + υ2Х) 0,5.	(16.8)

Направление суммарного перемещения определяется углом γ, углом наклона пере-

мещения к вертикальной оси

tg γ = υХ / υy = (PХ JХ) / (PyJy) = (PJХ sin α) / (PJy cos α) = (JХ / Jy) tg α.

(16.9)

46

Сравнивая соотношения (16.9) и (16.7) делаем вывод, что γ = β, как углы с взаимно

перпендикулярными сторонами. Следовательно, направление прогибов совпадает с

нормалью к нулевой линии и не совпадает с плоскостью действия сил. Последнее об-

стоятельство и послужило причиной для названия такого изгиба - косой изгиб.

Рассмотрим пример вычисления напряжений и прогибов при косом изгибе. Для

консоли, изображенной на рис. 16.2 примем следующие исходные данные: Р = 10 тс,

α = 450, ℓ = 2 м, h = 0,2 м, b = 0,1 м, модуль упругости материала Е = 21000000 тс/м2.

Требуется вычислить максимальные напряжения в сечении заделки, прогиб конца кон-

соли и направление прогиба.

Вычислим горизонтальную и вертикальную составляющие вектора сил:

РХ = Py= P sin 450 = 10 · 0,5· √2 = 7,071 тс.

Изгибающие моменты в заделке будут:

МХ = Мy = Py · ℓ = 7,071 · 2 = 14,142 тм.

Вычислим геометрические характеристики сечения:

JХ = b · h3/12 = (0,1 · 0,23) / 12 = 0,667 · 10-4 м4.

Jy = b3· h /12 = (0,13 · 0,2) / 12 = 0,167 · 10-4 м4.

WХ = 2 · JХ / h = 2 · 0,667 · 10-4 / 0,2 = 0,667 · 10-3 м3.

Wy = 2 · Jy / b = 2 · 0,167 · 10-4 / 0,1 = 0,333 · 10-3 м3.

Теперь вычислим напряжения в характерных точках сечения с помощью соотношений

(16.3) и (16.4). Максимальные напряжения растяжения возникают в точке С, а сжатия в точке А:

σС = MХ / WХ +My / Wy = 14,142 · 103/ 0,667 + 14,142 · 103 / 0,333 = 63607,2 тс/м2 = = 6360,7 кгс/см2.

В силу симметрии рассматриваемого сечения минимальные напряжения (сжатие) в

точке А: σА = - σС = - 6360,7 кгс/см2.

Напряжения в точке D:

σD = - MХ / WХ + My / Wy = - 14,142 · 103/ 0,667 + 14,142 · 103 / 0,333 = = 21202,4 тс/м2 = 2120,2 кгс/см2.

В точке В:

σВ = MХ / WХ - My / = 14,142 · 103/ 0,667 - 14,142 · 103 / 0,333 = - 21202,4 тс/м2 =

= - 2120,2 кгс/см2.

47

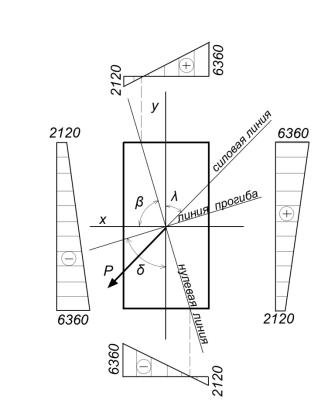
Вычислив напряжения в крайних точках сечения можно построить эпюры нормальных напряжений по граням сечения. Теперь можно графически построить линию нулевых напряжений. Если снести нулевые точки эпюр на грани сечения получим на этих гра-

нях следы нулевой линии. Соединив их, получим положение нулевой линии, рис. 16.5.

Рис. 16.5. Напряженное состояние сечения при косом изгибе

Далее вычислим аналитически угол наклона нулевой линии к оси Х, tg β = (JХ/ Jy) tg α = (0,667 · 10-4 / 0,167 · 10-4) · 1 = 4, откуда β ≈ 760.

Прогиб на конце консоли можно вычислить по соотношению (14.8):

υХ = PХℓ3/ (3 Е Jy) = 7,071· 23 / (3 · 21000000 · 0,167 · 10-4) = 0,05376 м = 5,376 см.

υy = Py ℓ3/ (3 Е JХ) = 7,071· 23 / (3 · 21000000 · 0,667 · 10-4) = 0,01344 м = 1,344 см.

υ= (υ2y + υ2Х) 0,5 = (5,3762 + 1,3442)0,5 = 5,541см.

Тангенс угла наклона плоскости перемещения к вертикальной оси tg γ = υХ / υy = 5,376 / 1,344 = 4. Откуда γ ≈ 760.

Таким образом, вычисления подтвердили, что направление перемещения перпендику-

лярно нейтральной линии: γ = β.

Лекция 17.

Внецентренное сжатие-растяжение. Определение напряжений в стержнях при

48

внеценренном действии продольной силы

Еще один случай сложного сопротивления возникает тогда, когда сжимающая или растягивающая сила, параллельная оси бруса, приложена не в центре тяжести его поперечного сечения. Такое напряженное состояние называется внецентренным сжа-

тием или растяжением. Далее мы будем рассматривать только сжимающую силу, имея в виду, что для растяжения действуют те же законы, только результирующие напряже-

ния следует брать с обратным знаком. Итак, для простоты, рассмотрим брус прямо-

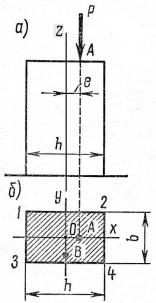
угольного сечения , который находится под действием сжимающей силы Р, рис. 17.1,

приложенной в плоскости ZOX, одной из главных осей инерции сечения, на некото-

ром расстоянии от центра тяжести. Расстояние e от точки приложения силы до центра тяжести сечения называется эксцентриситетом. Силу Р, приложенную с эксцентри-

ситетом, можно заменить эквивалентной ей системой - силой такой же величины, при-

ложенной в центре тяжести сечения и моментом Мy = Р ex. Очевидно, что центрально приложенная сила будет равномерно сжимать брус, а момент будет его изгибать. Если пренебречь горизонтальным перемещением верха бруса под действием изгибающего момента, то для вычисления напряжений в нем можно воспользоваться принципом не-

зависимости действия сил. Если пренебречь собственным весом бруса, то в любом его сечении, с координатой z по высоте, действуют внутренние усилия: нормальная сила

N = - P и изгибающий момент My = P ex= N ex.

Рис. 17.1. Внецентренно нагруженный стержень

Другими словами, мы получили сочетание центрального сжатия и чистого изгиба. Ве-

личина нормального напряжения в любом сечении бруса, на расстоянии x от оси Y,

определится как сумма двух напряжений

	49
σx = - N / F ± Мy · х / Jy = - N / F ± N ex · х / Jy,	(17.1)

где: F - площадь поперечного сечения бруса; Jy - момент инерции сечения относи-

тельно оси Y.

В случае приложения силы в плоскости другой главной оси инерции сечения ZOY, в

точке В, рис. 17.1, напряжения будут

σy = - N / F ± Мx · y / Jx = - N / F ± N eу· y / Jx,

(17.2)

где: Мx = P ey = N ey - изгибающий момент в плоскости ZOY; y - расстояние точки приложения силы от оси Х; Jx - момент инерции сечения относительно оси Х.

Наибольшие напряжения в сечении возникают на его гранях, поэтому для граней, соот-

ношение для напряжений (17.1) можно представить в виде:

σmax,min = - N / F ± My / Wy,

и так как Wy = b h2 / 6, F = b h, то выражение для максимальных напряжений будет

σmax,min = - N	/ F ± N 6 ex / (b h2) = - N / F · (1 ± 6 ex / h).	(17.3)
Анализ соотношения (17.3)	показывает, что знак напряжения зависит от выражения

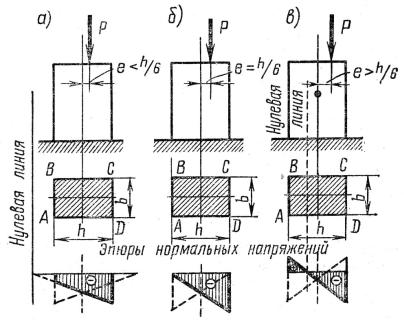
Рис. 17.2. К построению эпюр напряжений при внецентренном сжатии в скобках и здесь возможны три случая, см. рис. 17.2:

а) 6 ex / h < 1 или, что то же, ex < h / 6.

В этом случае выражение в скобках в соотношении 17.3 может быть только положительным, напряжения от изгиба по абсолютному значению будут меньше на-

пряжений от сжатия и следовательно, в сечении будут действовать только сжимающие напряжения, эпюра этих напряжений представлена на рис. 17.2 а. Если графически до-

50

строить эпюру для получения нулевого напряжения, то видно, что линия нулевых на-

пряжений будет расположена за пределами сечения.

б) 6 ex / h = 1 или ex = h / 6.

При таких условиях выражение в скобках может быть или равным нулю или положи-

тельным, т.е. напряжения в сечении будут одного знака. Максимальное напряжение,

напряжение по грани АВ сечения, рис. 17.2 б:

σmax = - N / F · (1 - 6 ex / h) = 0,

минимальное напряжение (по грани CD) будет

σmin = - N / F · (1 + 6 ex / h) = - 2 N / F = - 2 P / F.

Нулевая линия в этом случае проходит по грани сечения, а на противоположной грани напряжения сжатия в два раза больше напряжений, вызванных действием центральной сжимающей силы.

в) 6 ex / h > 1 или ex > h / 6.

При таком эксцентриситете выражение в скобках, и следовательно напряжения могут быть разнозначными, как положительными, так и отрицательными. Напряжения от из-

гиба на гранях сечения по абсолютной величине будут больше напряжений сжатия. По-

этому в одной части сечения будет действовать растяжение, в другой сжатие и нулевая линия будет расположена в пределах сечения, рис. 17.2 в. Заметим, что на этом рисунке для всех рассмотренных случаев пунктирными линиями показаны эпюры напряжений при приложении силы Р по другую сторону оси Y. Как видно, при зеркальном прило-

жении силы, зеркально изменяются и эпюры напряжений и положение нулевой линии.

Из анализа всех трех случаев приложения силы можно сделать такие выводы:

Если, при прямоугольном поперечном сечении, сила приложена в центре тяжести сече-

ния (в соотношении (17.1) ex = 0), то напряжения во всех точках сечении будут одина-

ковы и равны напряжениям центрального действия силы, а нулевая линия будет рас-

положена в бесконечности. Если теперь, перемещать точку приложения силы вдоль оси Х, то до тех пор, пока эта сила не выходит из пределов средней трети сечения, аб-

солютная величина эксцентриситета |ex| < h / 6, то напряжения во всем сечении будут одного знака, нулевая линия будет расположена вне пределов сечения, и по мере уве-

личения эксцентриситета, будет приближаться из бесконечности к грани сечения. Ко-

гда, эксцентриситет по абсолютной величине станет равен |ex| = h / 6, нулевая линия совпадет с гранью сечения (напряжения на этой грани будут равны нулю), а на проти-

воположной грани напряжения будут по абсолютной величине вдвое больше напряже-