Лекции по сопротивлению материалов II сем

21

связи и три опорных реакции), а правый конец, точка В, покоится на шарнирно под-

вижной опоре (одна элементарная связь и одна вертикальная реакция). Таким образом,

для определения опорных реакций мы имеем три уравнения равновесия и четыре неиз-

вестных в виде опорных реакций. Для определения реакции в лишней связи поступим следующим образом. Исходной балке, рис. 13.2 а, сопоставим балку, в которой лиш-

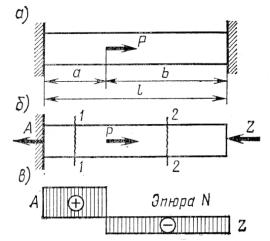
няя связь отброшена и заменена неизвестной опорной реакцией Х1, рис. 13.2 б.

Рис. 13.2. к определению реакции в лишней связи

Две эти балки отличаются друг от друга только тем, что правый конец исходной балки,

точка В не имеет вертикального перемещения υB = 0, а точка В второй балки переме-

щается под действием внешней нагрузки и реакции Х1. Для того, чтобы второе со-

стояние балки было эквивалентно первому, необходимо найти такую величину опор-

ной реакции Х1, при которой перемещение υB, правого конца балки было бы равно ну-

лю: υB = υBх + υBq = 0. (13.1)

Это условие и является дополнительным четвертым уравнением для определения ре-

акции Х1 в лишней связи. Определим перемещение υB. Для этого, приложим в точке B

единичную силу Х1 = 1, в данном случае, направленную вверх, рис. 13.2 б. Эпюра мо-

22

ментов М1 от действия этой единичной силы представлена на рис. 13.2 д. Там же пред-

ставлена эпюра моментов Мр от действия внешней нагрузки q на балку, освобожден-

ную от опоры В. Запишем уравнение 13.1, пользуясь интегралом Мора и правилом Ве-

рещагина

EJ υB =∫ М1M1· X1 dz + ∫ Мp M1 dz = X1 ℓ3/3 - qℓ4/8= 0,

(13.2)

ℓℓ

откуда получим: Х1 = 3 qℓ/8.

Определив значение лишнего неизвестного, можно построить исправленную эпюру мо-

ментов от действия опорной реакции в лишней связи - эпюра М1 Х1, рис. 13.2 д.

Окончательные эпюры моментов и поперечных сил можно построить, определив опор-

ные реакции в балке как в статически определимой системе.

Далее необходимо дать некоторые определения, поскольку использованная нами

методика имеет общий характер и используется для расчета много раз статически не-

определимых систем. Статически определимая система, которая получается из исход-

ной статически неопределимой, отбрасыванием лишних связей, называется основной системой. Уравнения типа (13.2), которые приводят основную систему к ограничени-

ям, накладываемым на статически неопределимую систему, называются уравнениями совместности перемещений. При составлении уравнений совместности перемещений принято придавать им определенную так называемую каноническую форму. Рассмот-

рим решение вышеприведенного примера с использованием ранее введенных (лекция

12)	обозначений. Перепишем соотношение (13.2) в виде
	1 = 1Х +	1P,		(13.3)
где:	1Х - перемещение точки B основной системы по направлению и под воздействи-
ем силы X1; 1P - перемещение этой же точки в направлении действия силы X1,				вы-
званное действием нагрузки P. Перемещение			1Х, исходя из (12.5) представим в виде
	1Х =	δ11 X1,		(13.4)
где δ11 - перемещение точки B основной системы в направлении действия силы X1,
вызванное единичной силой X1 = 1.
С учетом (13.4) уравнение (13.2) примет вид
	δ11 X1 +	1P	= 0.	(13.5)

Поскольку в уравнении (13.5) в качестве неизвестной величины выступает сила, это уравнение принято называть каноническим уравнением метода сил. Коэффициент при неизвестном δ11 и свободный (грузовой) член 1P в уравнении (13.5) с применением

	23
интеграла Мора определяются по соотношениям
δ11 = ∑ ∫ М12/(EJ) dℓ,	(13.6)
ℓ
1P =∑ ∫ М1 Мp /(EJ) dℓ,	(13.7)
ℓ
где знак ∑ означает, что в общем случае суммирование распространяется на все

стержни системы.

Предложенный подход применим также и к задачам о расчете статически неоп-

ределимых стержней, подверженных действию осевых нормальных сил. Рассмотрим

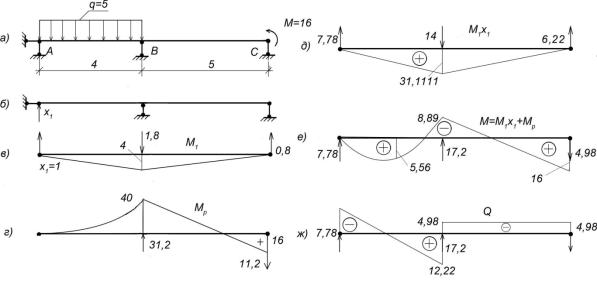
простейший пример. Горизонтальный невесомый стержень постоянного поперечного сечения, длиной ℓ, защемлен своими торцами в неподвижных опорах, рис. 13.3. На расстоянии α от левой опоры к стрежню приложена сила P. Требуется определить на-

пряжения в сечениях стержня. В стержне имеется одна лишняя связь, в правой опоре,

и одно лишнее неизвестное - реакция Z в ней. Основная система образуется отбрасы-

ванием лишней связи и ее заменщй действием неизвестной реакции Z, рис.13.3 б.

Запишем интеграл Мора для случая растяжения - сжатия,

= Nk Ni ℓ /(ЕF).

(13.8)

Рис. 13.3. Статически неопределимый стержень:

а - действительное состояние; б - основная система

Соответствующее каноническое уравнение (13.5) в этом случае примет вид

δ11 Z +	1P = 0.	(13.9)
Откуда пользуясь формулой Верещагина,	получим: ℓZ	+ αP = 0 и

Z = αP / ℓ.

Поскольку, А + Z = P, A = bP / ℓ. Напряжение в сечении 1 - 1, σ1 = bP / (ℓF);

в сечении 2 - 2, σ2 = αP / (ℓF).

24

Рассмотрим пример расчета один раз статически неопределимой балки. Пусть да-

на балка, схема которой приведена на рис. 13.4 а. Примем, что жесткость балки по дли-

не постоянна, поэтому множитель EJ исключаем из рассмотрения. Для раскрытия ста-

тической неопределимости будем применять различные основные системы.

Вариант I. Чтобы получить основную систему, отбросим опору А, заменив ее неиз-

вестной реакцией Х1. Получим балку пролетом ℓ = 5 м, с левой консолью длиной 4 м,

рис. 13.4 б. Приложим вместо неизвестной реакции Х1 единичную силу и построим эпюру моментов от ее действия. Эпюра моментов М1 и соответствующие опорные ре-

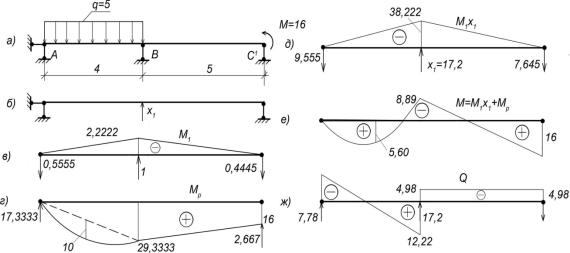
акции представлены на рис. 14.4 в. Далее приложим к основной системе действующие

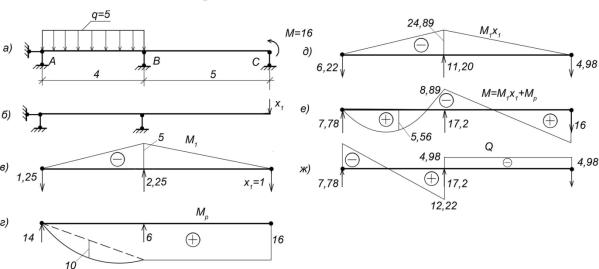
Рис. 13.4. К расчету статически неопределимой балки. Вариант I основной системы.

на балку усилия, вычислим опорные реакции и построим грузовую эпюру моментов

MP, рис. 13.4 г. Затем вычислим коэффициент при неизвестном и грузовой член кано-

нического уравнения 13.5:

δ11 = ∫ М12 dℓ = 0,5 · 4 · 4· (2/3) · 4 + 0,5 · 4 · 5· (2/3) · 4 = 48;

1P = ∫ М1 Мp dℓ = - (1/3) · 40 · 4 · (3/4) · 4 - (5/6) · (2 · 40 · 4 - 16 · 4) = - 373,(3).

Из канонического уравнения 13.5 получим: Х1 = - 1P	/ δ11 = 373,(3) / 48 = 7, 78.
Пересчитываем опорные реакции и эпюру моментов М1	от действия единичной силы,

умножением на вычисленное значение опорной реакции Х1 и строим пересчитанную эпюру М1 Х1, рис. 13.4 д. Складываем пересчитанную эпюру с эпюрой MP и получаем эпюру моментов М в заданной статически неопределимой балке. рис. 13.4 е. На этой же

25

эпюре приведены величины опорных реакций, также полученные путем суммирования.

Наконец строим эпюру поперечных сил, рис. 13.4 ж. Задача решена.

Вариант II. В качестве лишнего неизвестного выбираем вертикальную опорную реак-

цию в опоре В, отбрасываем эту опору и заменяем ее действие неизвестной силой Х1.

Основная система в данном случае представляет собой однопролетную балку пролетом

ℓ = 9 м, нагруженную внешней нагрузкой и неизвестной силой Х1 в месте нахождения опоры В, рис. 13.5 б. Эпюры моментов и опорные реакции от действия единичной М1 и

действительной нагрузок MP, приведены на рис. 13.5 в, г. Вычислим элементы канони-

ческого уравнения:

δ11 = ∫ М12dℓ = 0,5 · 2,222 · 4 · (2/3) · 2,222 + 0,5 · 2,222 · 5 · (2/3) · 2,222 = 14,814.

Для того чтобы подсчитать грузовой член канонического уравнения, криволинейную часть грузовой эпюры разделим на две составляющие - треугольник с вершиной равной

29,333 и параболу с проекцией основания равной 4, рис. 13.5 г. Высота этой параболы равна f= qℓ2пр /8. Здесь ℓпр - проекция криволинейного участка эпюры моментов на ось балки. В данном примере f= qℓ2пр /8 = 5 · 42/ 8 = 10. Вычислим грузовой член.

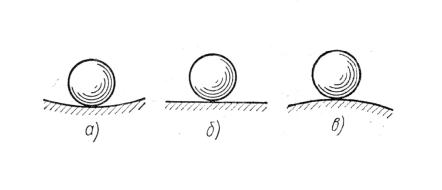
Рис. 13.5. Вариант II основной системы

1P = ∫ М1 Мp dℓ = - 0,5 · 29,333 · 4 · (2/3) · 2,222 + (2/3) · 10 · 4 · 0,5 · 2,222 - - (5/6) · (2 · 29,333 · 2,222 + 16 · 2,222) = - 254,81.

Следуя алгоритму вычислим: Х1 = - 1P / δ11 = 254,81 / 14,814 = 17,2. Исправленная эпюра моментов М1 Х1 и исправленные опорные реакции приведены на рис. 13.5 д.

Легко проверить, что суммирование эпюр и реакций даст результат, приведенный на рис. 13.4 е, ж.

26

Вариант III. В этом варианте основная система получается отбрасыванием лишней связи в опоре С и заменой ее неизвестной вертикальной силой Х1, направленной вниз,

рис. 13.6 б. Основная система является однопролетной балкой пролетом ℓ = 4 м с пра-

вой консолью длиной 5 м. Эпюра моментов и опорные реакции от действия единичной силы представлены на рис. 13.6 в, а грузовая эпюра на рис. 13.6 г.

Рис. 13.6. Вариант III основной системы

Вычислим значение лишней неизвестной:

δ11 = ∫ М12dℓ = 0,5 · 5 · 4 · (2/3) · 5 + 0,5 · 5 · 5 · (2/3) · 5 = 75.

1P = ∫ М1 Мp dℓ = - 0,5 · 16 · 4 · (2/3) · 5 + (2/3) · 10 · 4 · 0,5 · 5 -

- (5/6) · (2 · 16 · 5 + 16 · 5) = - 373,333.

Х1 = - 1P / δ11 = 373,333 / 75 = 4,98.

Исправленная эпюра моментов М1 Х1 и исправленные опорные реакции приведены на рис. 13.6 д. Суммируя эпюры и реакции получим уже тот же результат, рис. 13.4 е, ж.

Вариант IV. Образуем основную систему врезанием шарнира в балку, над опорой В.

Отметим, что во всех предыдущих вариантах основной системы механический смысл канонического уравнения состоял в том, что линейное вертикальное перемещение в месте отброшенной связи приравнивалось нулю. В рассматриваемом варианте встро-

енный шарнир позволяет торцам балки на опоре «B» поворачиваться относительно друг друга, а это нарушает принцип совместности перемещений - в балке не может быть перелома при упругом деформировании. Для исключения этого поворота, к тор-

цам обеих балок необходимо приложить изгибающие моменты Х1, рис. 13.7 б которые в совокупности с действующими нагрузками исключили бы этот взаимный поворот се-

27

чений. Таким образом, в роли лишнего неизвестного здесь выступает обобщенный из-

гибающий момент. Для раскрытия статической неопределимости прикладываем во встроенном шарнире изгибающий момент Х1 = 1. Дальнейшая процедура вычислений не отличается от предыдущих. Определяем опорные реакции и строим эпюру моментов в основной системе от действия единичного усилия, рис. 13.7 в. Вычисляем опорные реакции и моменты в основной системе от действия нагрузок, рис.13.7 г. Подсчитываем коэффициент при неизвестном и грузовой член канонического уравнения:

δ11 = ∫ М12dℓ = 0,5 · 1 · 4 · (2/3) · 1 + 0,5 · 1 · 5 · (2/3) · 1 = 3.

1P = ∫ М1 Мp	dℓ = - (2/3) · 10 · 4 · (1/2) · 1 - (1/2) · 16 · 5 · (1/3) · 1 = - 26,(6).
Х1 = - 1P / δ11	= 26,(6) / 3 = 8,89.

Далее пересчитываем единичную эпюру и получаем эпюру моментов М1 Х1 и соответ-

ствующие опорные реакции, рис. 13.7 д. Осталось сложить эту эпюру с эпюрой MP и

путем сложения вычислить опорные реакции. Получим результирующие величины представленные на рис. 13.4 е,ж.

Анализ процесса решения всех вариантов показывает что, наименее затратным по вычислениям и наиболее наглядным является последний вариант. Поэтому вариант введения шарнира для исключения лишних связей является предпочтительным.

Рис. 13.7. Вариант IV основной системы.

28

Лекция 14.

Устойчивость сжатых стержней. Устойчивое и неустойчивое равновесие. Понятие критической силы. Метод Эйлера для определения критических сил. Учет условий закрепления стержня. Понятие гибкости стержня.

Ранее, при проверке прочности сжатых стержней мы исходили из того условия, что несущая способность стержня будет исчерпана если напряжения в нем достигнут расчетного сопротивления материала на сжатие. Однако, экспериментально и теорети-

чески было доказано, что это условие справедливо только для коротких стержней.

Длинные стержни при действии увеличивающейся сжимающей силы сначала выпучи-

ваются, как при изгибе, затем поперечные перемещения быстро возрастают и стержень разрушается. Причем разрушение наступает при напряжениях меньших, чем предель-

ные напряжения из условия прочности по сжатию. Такое напряженное состояние длин-

ных стержней при центральном сжатии принято называть продольным изгибом, а по-

терю несущей способности стержня - потерей устойчивости прямолинейной формы сжатого стержня. Таким образом, можно отметить, что кроме проблемы прочности существует еще и проблема устойчивости отдельных элементов конструкции и кон-

струкции в целом. Необходимо дать определение понятию устойчивость. Любая систе-

ма, находящаяся в равновесии считается устойчивой, если при действии малого воз-

мущения она приобретает малые изменения, а при снятии этого возмущения возвраща-

ется в прежнее состояние равновесия. Система считается неустойчивой, если малое возмущение вызывает в ней большие изменения, а при снятии этого возмущения она или приобретает отличное, от начального состояния, равновесие или теряет равновесие.

Классическим примером устойчивого и неустойчивого состояния может служить рав-

новесие тяжелого шара покоящегося на вогнутой или выпуклой сфере и горизонталь-

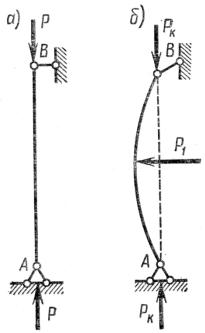
ной поверхности. В первом случае, рис. 14.1 а, при любом отклонении шар старается вернуться в первоначальное положение - шар находится в положении устойчивого рав-

новесия. В третьем случае, рис. 14.1 в, при любом

Рис. 14.1. К понятию устойчивости и неустойчивости систем

29

малом отклонении шар не вернется в исходную точку, а скатится в сторону, он нахо-

дится в состоянии неустойчивого равновесия. Шар, находящийся на горизонтальной поверхности, рис.14.1 б, будучи отклоненным, не вернется в исходное состояние, но и не будет двигаться далее - он находится в состоянии безразличного равновесия.

Рассмотрим понятие устойчивости применительно к центрально сжатым стерж-

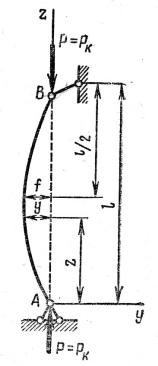
ням. Пусть длинный и тонкий вертикальный стержень, шарнирно закрепленный на опорах, центрально нагружен силой Р, которая статически возрастает, рис. 14.2 а. До достижения силой Р некоторой величины, стержень будет сохранять прямолинейную форму, а при отклонении его в горизонтальном направлении, возмущающей силой Р1,

рис. 14.2 б, он после удалении этой силы, снова вернет себе прямолинейную форму.

Такое равновесие стержня будет устойчивым. При дальнейшем увеличении силы Р,

достигается такое состояние, при котором слегка отклоненный в сторону стержень, по-

сле удаления силы Р1, уже не возвратится в прямолинейное положение, а останется ис-

кривленным. Прямолинейная форма стержня в данном случае будет неустойчивой.

Рис. 14.2. К понятию устойчивости при продольном изгибе Между этими двумя состояниями существует переходное критическое состояние,

при котором стержень может сохранить прямолинейную форму, а может при боковом воздействии приобрести устойчивую криволинейную форму. Наибольшая сжимающая сила, при которой стержень еще сохраняет устойчивость, называется критической си-

лой и обозначается как РК.

Зададимся вопросом: почему центрально нагруженные прямолинейные стержни теряют устойчивость. Они потому теряют устойчивость, что на практике невозможно

30

технически выполнить условия центрального сжатия. Во-первых, невозможно органи-

зовать приложение силы строго по оси стержня без эксцентриситета. Все стыковочные детали колонн выполняются с определенными допусками. Во-вторых, невозможно по-

лучить стержни с материалом со строго однородными свойствами, как по сечению, так и по длине стержней. По этим, а также по ряду других причин центральное сжатие стержней реализовать невозможно и при проектировании необходимо проверять проч-

ность и устойчивость стержней в условиях продольного изгиба. Для этого к проверке по прочности необходимо добавить еще проверку по критической силе, которую пока запишем в таком виде:

σ= РК / F ≤ Rрас .

(14.1)

Задача об определении критической силы была решена в 1774 г Леонардом Эйле-

ром. Повторим вывод формулы для критической силы. Пусть прямолинейный стер-

жень длиной ℓ закреплен шарнирно по концам и в токе В к нему центрально приложена вертикальная сила Р = РК, рис 14.3. Под действием этой силы стержень получает ис-

кривление в плоскости его минимальной жесткости и в этом состоянии он сохраняет

Рис. 14.3. К выводу формулы Л. Эйлера

равновесие, т.е. устойчивость. Изгибающий момент в любом сечении, на расстоянии z

от начала координат равен:

MZ = - PK · y. (14.2)

Знак минус здесь принят потому, что при принятом направлении оси У прогиб отрица-