Лекции по сопротивлению материалов II сем

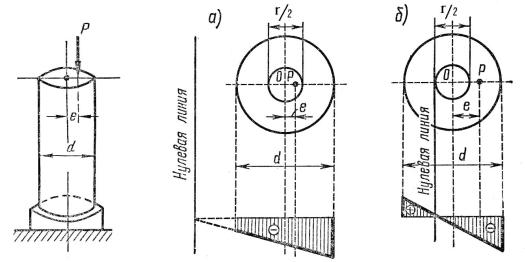
51

ний, возникающих при центральном приложении силы. При дальнейшем перемещении силы вдоль оси Х, когда точка приложения силы выйдет за пределы средней трети се-

чения, |ex| > h / 6, нулевая линия вступит в пределы сечения и напряжения в сечении станут разнозначными, часть сечения будет сжата, часть растянута.

Естественно, что все приведенные выше выводы справедливы и для случая приложения силы с эксцентриситетом вдоль оси Y.

Полученные результаты имеют большое прикладное значении. В несущих кон-

струкциях зданий в качестве колонн и межпроемных столбов применяются кирпич, ка-

менные материалы и бетон, т.е. материалы, плохо сопротивляющиеся растяжению. По-

этому, для таких конструкций необходимо так подбирать их размеры, чтобы исключить появление растягивающих напряжений. В частности, для прямоугольных столбов и ко-

лонн необходимо обеспечить такие условия, чтобы точка приложения сжимающей си-

лы была расположена в пределах средней трети сечения.

Рассмотрим теперь колонну круглого сечения эксцентрично нагруженную про-

дольной силой Р, рис. 17.3. Площадь поперечного сечения колонны F = π r2, осевой

момент сопротивления W = π r3/ 4, следовательно, напряжения в крайних волокнах будут

σmax,min = - P/ F ±M / W = - P/(π r2) ± 4 Pe/(π r3) = - P/ (π r2) · (1 ± 4e / r ). (17.4)

Рис. 17.3 К определению напряжений в круглой колонне нагруженной эксцентрично

анализ формулы (17.4) показывает, что если эксцентриситет e < r / 4, то напряжения в

сечении будут одного знака, а в случае, если e > r / 4, напряжения будут разнозначны,

часть сечения будет сжата, часть растянута и нулевая линия пройдет через сечение. Для того , чтобы при сжимающей силе, в сечении колонны не возникало растягивающих

52

напряжений точка приложения силы не должна выходить из круга диаметром равным половине радиуса колонны. Граничным будет случай, когда эксцентриситет e = r / 4,

тогда нулевая линия коснется края колонны, а на другом крае напряжения будут равны удвоенным напряжениям при действии центрально расположенной силы.

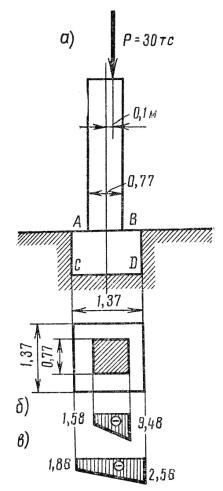
Рассмотрим практический пример. Требуется проверить прочность квадратного

кирпичного столба, опирающегося на квадратный бетонный фундамент и несущую способность грунта основания под фундаментом, рис. 17.4. На верх кирпичного столба действует сила Р = 30 тс, приложенная с эксцентриситетом ex = 0,1 м. Другие исходные данные: высота столба hc = 3 м, сечение столба 0,77 х 0,77 м, расчетное сопротивление кирпичной кладки Rк = 10 кгс/см2, объемный вес кирпичной кладки γк = 1,6 тс/м3, вы-

сота фундамента hф = 0,5 м, поперечное сечение фундамента 1,37 х 1,37 м, объемный

вес бетона γб = 2,2 тс/м3,	расчетное сопротивление грунта основания Rгр = 3 кгс/см2.
	Р е ш е н и е. Площадь поперечного сечения
	столба Fc = 0,77 · 0,77 = 0,593 м2.
	Площадь подошвы фундамента
	Fф = 1,37 · 1,37 = 1,88 м2.
	Изгибающий момент
	My = P ex= 30 · 0,1 = 3 тсм.
	Момент сопротивления столба относительно оси Y
	Wcy =0,77 · 0,772/6 = 0,0761 м3.
	Момент сопротивления площади фундамента
	W = 1,37 · 1,372/6 = 0,429 м3.
	фу
	Определяем напряжения в основании кирпичного
	столба с учетом собственного веса (сечение А В)
	σmax = - (Р / Fф + hc γк) +My / Wcy =
	= - (30/0,593 + 3·1,6) + 30 · 0,1 / 0,0761 = -15,8 тс/м2,
	σmax = - 1,58 кгс/см2,
	σmin = - (Р / Fф + hc γк) - My / Wcy =
	= - (3/0,593 + 3 · 1,6) - 30 · 0,1 / 0,0761 = - 94,8 тс/м2,
Рис. 17.4	σmin = - 9,48 кгс/см2.

Определяем напряжения под подошвой фундамента с учетом собственного веса конст-

53

рукций (сечение C D)

σmax = - ((Р + Fc hc γк)/ Fф + hф γф) +My / Wфy =

= - ((30 + 0,593 · 3 · 1,6) / 1,88 + 0,5 · 2,2) + 30 · 0,1 / 0,429 = - 18,57 тс/м2,

σmax = - 1,86 кгс/см2.

σmin = - ((Р + Fc hc γк)/ Fф + hф γф) -My / Wфy =

= - ((30 + 0,593 · 3 · 1,6) / 1,88 + 0,5 · 2,2) - 30 · 0,1 / 0,429 = - 25,56 тс/м2,

σmin = - 2,56 кгс/см2.

Как видно из решения, условия прочности не нарушены как по кладке

Rк = 10 > |σmin|= 9,48 кгс/см2 ,

так и по несущей способности грунта основания

Rгр = 3 > |σmin|= 2,56 кгс/см2.

Лекция 18.

54

Определение положения нулевой линии при внецентренном сжатии-растяжении. Ядро сечения.

Ранее, нами рассматривались случаи, когда нормальная сила действовала в плос-

кости одной из главных осей координат сечения. Рассмотрим теперь случай, когда нормальная сила действует в произвольной точке прямоугольного сечения, в плоско-

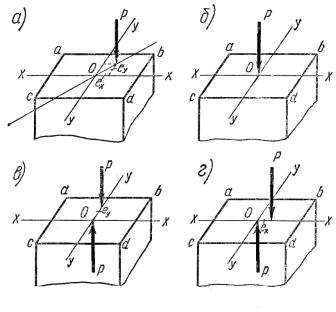
сти, которая не совпадает ни с одной из главных плоскостей. Пусть сжимающая сила Р приложена в точке поперечного сечения с координатами ex и eу, рис. 18.1 а. От дейст-

вия этой силы

Рис. 18.1. Действие нормальной силы в произвольной точке сечения

в произвольном сечении возникают усилия: продольная сила N и изгибающие момен-

ты Mх и My

N = - Р; Mх = - Р eу; My = - Р eх.

(18.1)

Другими словами, напряженное состояние сечения при действии силы Р, приложенной с произвольным эксцентриситетом можно заменить тремя составляющими: напряже-

ниями сжатия от силы Р, приложенной в центре тяжести сечения, рис. 18.1 б, и напря-

жениями, вызванными двумя изгибающими моментами Mх и My от сил, приложен-

ных с эксцентриситетами ex и eу, рис. 18.1 в,г. Нормальное напряжение σ в произ-

вольной точке сечения с координатами х и у при этом будет

σ = - N / F ± Мx · y / Jx ± Мy · х / Jy.

(18.2)

Выбор знаков в соотношении (18.2) зависит от характера напряжений: растяжение при-

нимается со знаком «+», сжатие со знаком «-». Наибольшие напряжения в сечениях имеющих две оси симметрии возникают на гранях сечения и вычисляются по формуле

	55
σmax,min = - N / F ± Mх / Wх ± My / Wy.	(18.3)

Напряжения в вершинах прямоугольника, в точках а, b, c, d будут:

σа = - N / F - Mх / Wх + My / Wy,

σв = - N / F - Mх / Wх - My / Wy,

σс = - N / F + Mх / Wх + My / W,.

σd = - N / F + Mх / Wх - My / Wy.

Попробуем теперь определить положение нулевой линии, т.е. линии на которой нормальные напряжения равны нулю. Для этого перепишем выражение для напряже-

ний (18.2) с учетом соотношений (18.1) и соотношения для момента инерции сечения через площадь и радиус инерции J = F i2:

σ = Р / F + Р eу · y / (F ix2) + Р eх · х / (F iy2) или
σ = (Р / F) (1 + eу · y / ix2 + eх · х / iy2).	(18.4)
В этом соотношении приняты положительные знаки перед всеми его членами,	так как

знак напряжений определяется знаком силы Р и знаками координат x и y. Формула

(18.4) позволяет определять нормальные напряжения в любой точке сечения. Для опре-

деления нулевой линии приравняем правую часть соотношения (18.4) нулю. Так как

Р ≠ 0 и F ≠ 0, получим:
1 + eу · yN / ix2 + eх · хN / iy2 = 0,	(18.5')
где хN, yN - текущие координаты нулевой линии.
Перепишем последнее соотношение в виде:
yN = - ix2/ eу – (eх · ix2 / (eу · iу2)) хN.	(18.5)

Соотношение (18.5) и есть уравнение нулевой линии. Как видно из этого уравнения,

нулевая линия представляет собой прямую, которая на оси X (при yN = 0) отсекает от-

резок αN, а на оси Y (при хN = 0) отрезок bN

αN = - iу2 / eх, bN = - ix2/ eу,

(18.6)

а тангенс угла наклона нулевой линии к оси Х будет равен отношению этих отрезков

tg α = bN / αN = (ix / iу)2 (eх / eу).

(18.7)

Из приведенных соотношений ясно, что положение нулевой линии зависит от эксцен-

триситета приложения силы, формы и размеров сечения и не зависит от величины си-

лы. Из соотношений (18.6) можно получить обратные соотношения которые позволя-

ют, зная положение нулевой линии, определить координаты точки приложения силы

		56
eх = - iу2 / αN;	eу = - ix2/ bN.	(18.8)
Воспользуемся соотношениями (18.6)	для установления связи между точкой приложе-
ния силы и положением нулевой линии. Приложим силу на оси Х (eу = 0)		в точке 1

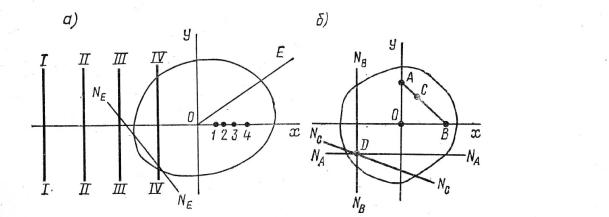
поперечного сечения стержня, рис 18.2 а. Тогда bN = - ix2/ eу = bN = - ix2/ 0 = ∞ и это означает, что нулевая линия параллельна оси Y и занимает положение I - I. Если теперь перемещать силу по оси Х помещая ее последовательно в точки 2, 3 и 4, нулевая линия будет перемещаться параллельно самой себе, приближаясь к центру тяжести сечения,

и будет последовательно занимать положение II-II, III-III и IV-IV, рис. 18.2 а.

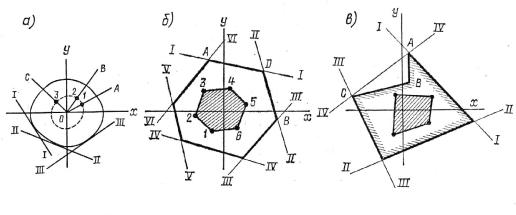
Рис. 18.2. К установлению взаимосвязи точки приложения силы и нулевой линии Рассмотрим теперь случай, когда сила Р будет перемещаться от центра тяжести сечения к его периферии по некоторой произвольной прямой ОЕ, рис. 18.2 а. В этом случае ну-

левая линия NE также буде перемещаться из бесконечности к центру тяжести сечения параллельно самой себе. Представим себе другой случай. Пусть точка приложения си-

лы Р перемещается по некоторой прямой АВ, которая не проходит через центр тяжести сечения, рис. 18.2 б. Если сила приложена в точках А или В, в местах пересечения линии АВ с осями координат Х и Y, то соответствующие нулевые линии NA и NB бу-

дут параллельны осям Х и Y. Предположим, что эти нулевые линии пересекаются в точке D. Так как, эта точка одновременно принадлежит двум нулевым линиям, то если мы одновременно приложим сжимающие силы в точках А и В, напряжения в токе D

также будут равны нулю. Приложим теперь силу в произвольной точке С, лежащей на прямой АВ. Эту силу можно разложить на две статически эквивалентные составляю-

щие РА и РВ, приложенные в точках А и В. Но ранее было показано, что в этом случае напряжения в точке D равны нулю. Следовательно, при перемещении силы по прямой от точки А к точке В напряжения в точке D всегда равны нулю. Что же касается нуле-

вой линии, то вначале движения силы, когда точкой ее приложения была точка А, ну-

левая линия была горизонтальной, а когда сила переместилась в точку В, нулевая ли-

57

ния, проходя через точку D, стала вертикальной. Отсюда следует, что при движении точки приложения силы от точки А к точке В по прямой линии, нулевая линия враща-

ется вокруг точки D. Полученные в ходе предыдущего анализа результаты позволяют нам сделать в дальнейшем некоторые важные выводы.

Рассмотрим колонну с поперечным сечением произвольной формы, рис. 18.3 а.

Рис. 18.3. К обоснованию понятия «ядро сечения» Предположим, что сила Р перемещается от центра тяжести сечения к его периферии по прямой ОА, следовательно соответствующая нулевая линия I-I будет перемещаться из бесконечности в сторону центра тяжести сечения и когда она коснется сечения сила будет приложена в точке 1, рис. 18.3 а. Если переместить силу по прямой ОА за точку

1, то нулевая линия пересечет контур сечения и разделит его на две части - в одной из них сечение будет сжато, в другой растянуто. Другими словами, точка 1 служит неко-

торой границей. Если сжимающая сила приложена до этой точки со стороны центра тяжести, все сечение будет сжато, если после этой точки, то часть сечения будет рас-

тянуто. Точно также можно определить граничные точки 2 и 3 на осях ОВ и ОС и со-

ответствующие им нулевые линии II-II и III-III. Если теперь провести вокруг центра тяжести множество лучей и на каждом из них отметить граничные точки, то можно по-

лучить границу некоторой области, которая называется ядром сечения.

Ядром сечения называется такое геометрическое место точек поперечного се-

чения, которое характерно тем , что любая продольная сила, приложенная в его гра-

ницах, вызывает в сечении напряжения одного знака.

Для того, чтобы построить ядро сечения необходимо рассмотреть множество ка-

сательных к контуру сечения, отождествляя эти касательные с нулевыми линиями, и

для каждой такой касательной найти внутри сечения соответствующую точку прило-

жения силы, т.е. граничные точки ядра сечения. Соединяя затем эти граничные точки,

получим ядро сечения. Для примера рассмотрим сечение в виде произвольного много-

угольника, рис. 18.3 б. Предположим сначала, что нулевая линия I-I совпадает со сто-

58

роной AD. Зная расположение этой линии, определим отрезки, которые она отсекает на координатных осях αN и bN, а затем по соотношениям (18,8) и координаты соответ-

ствующей точки границы ядра сечения. В данном примере это будет точка 1. Обходя контур сечения, и повторяя описанные операции, получим остальные точки ядра сече-

ния от 2 до 6. Соединяя полученные точки прямыми линиями, получим ядро сечения.

Из этого примера видно также, что если сечение имеет форму многоугольника, то и ядром сечения также будет многоугольник с таким же числом сторон. Однако это пра-

вило распространяется только на выпуклые многоугольники. Из рис. 18.3 в, видно, что если многоугольник имеет впадающие углы, то ядро сечения не будет иметь то же чис-

ло сторон. Это происходит потому, что ядро сечения всегда представляет собой выпук-

лый многоугольник. Действительно, если провести нулевую линию по одной из впа-

дающих сторон (стороны CD или AB на рис. 18.3 в) то эта линия пройдет через часть сечения и, следовательно, соответствующая ей сила вызовет в сечении напряжения разного знака.

Рассмотрим несколько примеров построения ядра сечения для некоторых рас-

пространенных форм поперечных сечений.

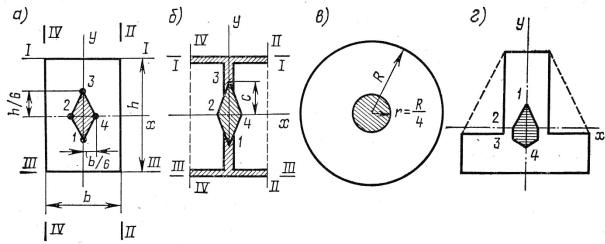
1. Прямоугольное сечение со сторонами h и b, рис. 18.4 а. Рассмотрим четыре положе-

ния касательной, совпадающие со сторонами прямоугольника. Для касательной I-I

Рис. 18.4. Построения ядра сечения для различных поперечных сечений:

а- прямоугольный брус; б - сечение стального прокатного двутавра; в - круг;

г- тавр с нижней полкой

отрезки, отсекаемые ею на осях координат, будут, учитывая, что i2 = J / F:

eх = - iу2 / αN = - iу2 / ∞ = 0; eу = - ix2/ bN = - 2 Jx / (h F) = 2 b h3 / (12 b h2) = - h / 6.

Т.е. точка 1 лежит на оси Y на расстоянии eу = h / 6 от центра тяжести сечения в сто-

рону противоположную касательной. Повторив рассуждения для касательной III-III,

59

получим, что точка 3 ядра сечения расположена на расстоянии eу = h / 6 вверх от цен-

тра тяжести сечения. По аналогии для сторон II-II и IV-IV получим eх = ± b / 6. Со-

единив между собой точки, получим ядро сечения. Для прямоугольника оно имеет форму ромба. Из рассмотренного примера можно также сделать вывод, что для сече-

ний обладающих двойной симметрией достаточно определить только половину точек ядра сечения.

2. Сечение прокатного двутавра. В общем случае имеется четыре границы сечения, но в силу симметрии определим положение только двух точек ядра сечения. Для точек, рас-

положенных на оси Y имеем из (18.8)

eу = ± ix2/ (h / 2),

а для точек ядра на оси Х

eх = - iу2 / (b / 2).

Величины радиусов инерции ix и iy берутся из сортамента прокатных стальных изде-

лий. Форма ядра сечения для двутаврового сечения также представляет собой ромб. 3. Круглое сечение. Ввиду круговой симметрии достаточно определить одну точку яд-

ра сечения

e = i2 / R = J / (F R) = π R4 / (4πR2 R) = R / 4.

Для круга, ядро сечения представляет собой круг диаметром равным четверти радиуса. 4. Тавровое сечение. На рис. 18.4 г, без вычислений показана форма ядра сечения для тавра с нижней полкой. Ясно, что это ядро должно представлять собой шестиугольник симметричный относительно оси Y.

60

ЛИТЕРАТУРА

1.Сопротивление материалов. Учебник, под общей редакцией А.Ф. Смирнова.

–М.: «Высшая школа», 1975.

2.П.А. Степин. Сопротивление материалов. Учебник.

–СП-М-Кр.: «ЛАНЬ», 2010.

3.В.Н. Сидоров. Лекции по сопротивлению материалов и теории упругости.

-М.: Редакционно-издательский центр Генерального штаба ВС РФ, 2002.

4.Н.С. Улитин. Сопротивление материалов. Учебник.

–М.: «Высшая школа», 1975.

5.Г.С. Варданян, Н.М. Атаров, А.А. Горшков. Сопротивление материалов с основами строительной механики. Учебник. - М.: ИНФРА, 2011.

6.А.Я. Астахова. Рабочая тетрадь для лекций и практических занятий по сопротивлению материалов. Часть 2. МАРХИ. – М.:, 2012.