Лекции по сопротивлению материалов II сем

1

МОСКОВСКИЙ АРХИТЕКТУРНЫЙ ИНСТИТУТ

(Государственная академия)

Кафедра « Высшая математика и строительная механика»

Сопротивление материалов

Конспект курса лекций для студентов II курса ( 4 –й семестр)

Составил: профессор, докт. техн. наук, Л. И. ЯРИН

М О С К В А 2011

2

СОДЕРЖАНИЕ

	стр.
Лекция 11.	Перемещения в балке при изгибе. Дифференциальное уравнение	3
	оси изогнутого бруса. Определение перемещений в балках путем
	непосредственного интегрирования дифференциального
Лекция 12.	уравнения изгиба.
	Теоремы о взаимности работ и перемещений. Определение	10
	линейных и угловых перемещений в балках по формуле Мора.
Лекция 13.	Правило Верещагина для перемножения эпюр.
	Простейшие статически неопределимые балки и стержни. Степень	20
	статической неопределимости, определение «лишних» связей. Выбор
Лекция 14	основной системы. Уравнения совместности деформаций.
	Устойчивость сжатых стержней. Устойчивое и неустойчивое	28
	равновесие. Понятие критической силы. Метод Эйлера для
	определения критических сил. Учет условий закрепления стержня.
	Понятие гибкости стержня.
Лекция 15.	Пределы применимости формулы Эйлера. Проверка устойчивости	34
	стержней. Подбор сечений стержней по устойчивости. Примеры.
Лекция 16.	Сложное сопротивление. Косой изгиб. Расчет балок при косом изгибе.	41
Лекция 17.	Понятие нулевой линии. Вычисление прогибов при косом изгибе.
	Внецентренное сжатие-растяжение. Определение напряжений в	48
Лекция 18.	стержнях при внеценренном действии продольной силы.
	Определение положения нулевой линии при внецентренном	54
	сжатии-растяжении. Ядро сечения.
Литература		60

3

Лекция 11

Перемещения в балке при изгибе. Дифференциальное уравнение оси изогнутого бруса. Определение перемещений в балках путем непосредственного интегрирования дифференциального уравнения изгиба.

Для нормальной эксплуатации балочной конструкции необходимо обеспечить не только ее прочность, но и необходимую жесткость. На практике это достигается тем,

что максимальный прогиб υmax, т.е. максимальное вертикальное перемещение изогну-

той оси балки ограничивается строительными нормами. Обычно ограничивают относи-

тельный прогиб - отношение максимального прогиба υmax к пролету ℓ

υmax / ℓ ≤ [υ / ℓ],

(11.1)

где [υ / ℓ] нормируемая величина: допустимый относительный прогиб.

Для различных условий эксплуатации балок величина допустимого прогиба колеблется в пределах от 1/150 до 1/1000. Естественно, что для проверки жесткости балки необхо-

димо научиться определять перемещения точек ее оси. Здесь мы будем рассматривать плоский изгиб, т.е. случай, когда поперечное сечение балки имеет вертикальную ось симметрии и действующие на балку усилия расположены в плоскости этой симметрии.

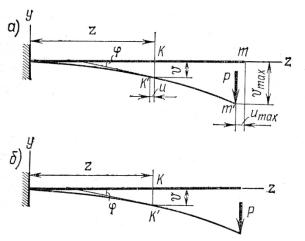
Рассмотрим балку в виде консоли, изображенную на рис. 11.1. Эта балка изгиба-

ется под воздействием сосредоточенной силы Р, приложенной к ее концу в точке m.

Рис. 11.1 Деформирование консольной балки при изгибе:

а- схема перемещений при изгибе; б - расчетная схема

Врезультате изгиба ось балки искривляется. Произвольная точка К, отстоящая от за-

делки на расстоянии z переместится в точку К′, рис. 11.1 а. Обозначим вертикальное перемещение произвольной точки К оси бруса через υ, а горизонтальное через u. Если в точке К′ провести касательную к изогнутой оси балки, то по отношению к исходному положению оси она будет повернута на угол φ. Величины υ, u и φ, в общем случае,

4

являются компонентами перемещения поперечного сечения балки. Сразу отметим, что горизонтальное перемещение u имеет более высокий порядок малости, чем вертикаль-

ное перемещение υ и угол φ, поэтому этим перемещением мы пренебрегаем, и в даль-

нейшем будем считать, что все точки оси балки перемещаются строго вертикально, а

угол наклона касательной к изогнутой оси балки равен углу наклона поперечного сече-

ния к первоначальному положению, рис. 11.1 б. Эти допущения естественно вытекают из принятой ранее предпосылки о малости перемещений в сопротивлении материалов.

Таким образом, задача сводится к нахождению величин υ и φ.

Для определения перемещений балки обратимся к полученному нами ранее со-

отношению между изгибающим моментом и кривизной
1 / ρ = M / (Е J).	(11.2)

Из аналитической геометрии известно, что кривизна кривой выражается следующим соотношением

1 / ρ = (d2υ /dz2)/ [1 + (dυ/dz)2]3/2.

(11.3)

Подставляя (11.3) в (11.2) получим точное дифференциальное уравнение изогнутой оси балки (уравнение упругой оси)

(d2υ /dz2)/ [1 + (dυ/dz)2]3/2 = M / (Е J) .

(11.4)

Однако, в силу принятых допущений о малости перемещений dυ/dz = φ = tg φ и квад-

ратом первой производной dυ/dz можно пренебречь как величиной второго порядка малости по сравнению с единицей в и в дальнейшем пользоваться приближенным дифференциальным уравнением изогнутой оси балки

d2υ /dz2 = ± M/ (Е J).

(11.5)

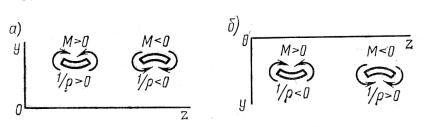
Выбор знака в соотношении (11.5) зависит от выбора системы координат, так как знак изгибающего момента может не совпадать со знаком кривизны. Знак изгибающего мо-

мента мы принимаем в зависимости от положения растянутого волокна балки,

Рис. 11.2. К соотношению знаков кривизны и изгибающих моментов

а знак кривизны определяется направлением оси Оу, рис.11.2. Так, когда ось у направ-

лена вверх, положительному моменту соответствует положительная кривизна, а отри-

5

цательному моменту - отрицательная, а при оси Оу направленной вниз положительно-

му моменту соответствует отрицательная кривизна, а отрицательному моменту поло-

жительная, рис. 11.2 б. Следовательно, в первом случае в соотношении (11.5) всегда выбирается знак плюс , а во втором - знак минус. Правая часть этого соотношения яв-

ляется известной функцией от координаты z, поэтому имеем дело с простым диффе-

ренциальным уравнением. Проинтегрируем его один раз и мы получим выражение для вычисления углов поворота сечений

φ = dυ/dz = ∫ M / (Е J) dz + С,

(11.6)

где С - произвольная постоянная интегрирования.

После повторного интегрирования находим выражение для вертикального перемеще-

ния точек оси балки

υ = ∫∫ M / (Е J) dz dz + Сz + D.

(11.7)

Постоянные интегрирования C и D находятся из граничных условий, которые зависят от вида опор балки, т.е. от способа закрепления ее концов. Естественно, что для вычис-

ления перемещений необходимо получить аналитическое выражение для изгибающего момента М.

Рассмотрим несколько примеров вычисления перемещений.

1. Вычислим прогиб и угол поворота сечения в произвольной точке консольной балки,

нагруженной сосредоточенной силой, рис. 11.3. Ось у направим вверх. Для нахождения

Рис. 11.3. Вычисление перемещений в консольной балке

изгибающего момента рассмотрим равновесие правой отсеченной части балки на рас-

стоянии zот левой опоры: М = - Р (ℓ - z). Знак минус соответствует тому, что растяну-

тыми являются верхние волокна балки. Подставим выражение для изгибающего мо-

мента в соотношение (11.5). Оно примет вид

d2υ /dz2 = - Р (ℓ - z)/ (Е J).	(11.7)
Если считать жесткость балки постоянной, тогда интегрируя один раз, получим
φ = dυ/dz = - Р ℓ z / (Е J) + Р z2 / (2Е J) + С.	(11.8)
Для вычисления υ интегрируем еще раз

		6
υ = - Р ℓ z2 / (2Е J) + Р z3 / (6Е J) + С z + D.		(11.9)
Определим теперь постоянные интегрирования из граничных условий . В заделке
при z = 0	φ = dυ/dz = 0, следовательно, из (11.8)	С = 0,
при z = 0	υ = 0, следовательно, из (11.9) и D = 0.
Окончательно имеем
φ = dυ/dz = - Р ℓ z / (Е J) + Р z2 / (2Е J).		(11.10)
υ = - Р ℓ z2 / (2Е J) + Р z3 / (6Е J).		(11.11)

В данном примере ясно, что максимальные значения перемещений будут иметь место на конце консоли при z = ℓ:

перемещение υℓ = - Р ℓ3/ (3Е J),

угол поворота сечения: φℓ = - Р ℓ2 / (2Е J).

Знак минус для величины υℓ означает, что вертикальное перемещение происходит против положительного направления оси у, т.е.вниз, а для угла поворота φℓ то, что ка-

сательная к изогнутой оси балки не расположена в положительном квадранте про-

странства (сечение поворачивается по часовой стрелке).

2. Определим прогибы и углы поворота сечений для балки на двух опорах, загруженной равномерно распределенной нагрузкой, рис. 11.4. Ось у направим вниз, поэтому в дифференциальном уравнении (11.5) перед правой частью следует принять знак минус.

Рис. 11.4. Перемещения в балке на двух опорах

Изгибающий момент в произвольном сечении с координатой z равен M = qℓz/2 - qz2/2.

Знак у изгибающего момента положительный, так как под действием нагрузки растяги-

ваются нижние волокна балки. Разрешающее дифференциальное уравнение можно за-

писать в следующем виде

(Е J) d2υ /dz2 = - qℓz/2 + qz2/2.	(11.12)
Последовательное интегрирование дает
(Е J) φ = (Е J) dυ/dz = - qℓz2/4 + qz3/6 + С,	(11.13)

	7
(Е J) υ = - qℓz3/12 + qz4/24 + Сz + D.	(11.14)

Определим постоянные интегрирования из граничных условий. На левой опоре балки

при z = 0, υ = 0, следовательно, из (11.14) и D = 0. На правой опоре при z = ℓ, υ = 0,

следовательно, из (11.14) - qℓ4/12 + qℓ4/24 + Сℓ = 0, откуда С = qℓ3/24. Подставляя найденные значения постоянных в выражения для υ и φ получим

(Е J) φ = (Е J) dυ/dz = qℓ3/24 - qℓz2/4 + qz3/6,	(11.15)
(Е J) υ = qℓ3z/24 - qℓz3/12 + qz4/24.	(11.16)

Последние соотношения позволяют вычислить перемещения и углы поворота в любом сечении. Отметим, что вертикальные перемещения получаются положительными, так как ось у направлена вниз, и направление перемещений совпадает с направлением оси.

Для того, чтобы найти максимальный прогиб и положение сечения с максималь-

ным прогибом, в общем случае, необходимо приравнять производную от функции про-

гибов υ нулю, т.е. приравнять нулю угол поворота сечения φ. В рассмотренном приме-

ре из условий симметрии можно видеть, что максимальный прогиб будет иметь место в середине пролета при z = ℓ/2

υmax = 5qℓ4/(384 EJ).	(11.17)
На опорах при z = 0 и z = ℓ угол поворота равен
φℓ,0 = ±qℓ3/(24Е J).	(11.18)

Рассмотренные выше примеры объединяет то, что изгибающий момент опреде-

ляется одним выражением по длине балки, т.е. балка с точки зрения эпюры моментов представляет собой один участок.

Рассмотрим далее пример вычисления перемещений в более сложном случае.

3. Определить перемещения и углы поворота сечений для балки на двух опорах, нагру-

женной сосредоточенной силой Р в середине пролета. При таком загружении изгибаю-

щий момент вычисляется различно на различных участках балки, рис. 11.5.

На первом участке при 0 ≤ z ≤ ℓ/2	М1 = Р z/2,
на втором участке при ℓ/2 ≤ z ≤ ℓ	М2 = Р (ℓ-z)/2.

Подстановка этих соотношений в дифференциальное уравнение изгиба (11.5) и после-

довательное интегрирование их дает

(Е J) φ1 = (Е J) dυ1/dz = Рz2/4 + С1,	(a)
(Е J) υ1 = Рz3/12 + С1z + D1,	(b)

	8
(Е J) φ2 = (Е J) dυ2/dz = - Рz2/4 + Рℓz/2 + С2,	(с)
(Е J) υ2 = - Рz3/12 + Рℓz2/4 + С2z + D2.	(d)

Рис. 11.5. К вычислению перемещений в балке на двух опорах, при действии сосредоточенной силы в середине пролета:

а - схема балки; б - максимальные перемещения

Для определения четырех постоянных интегрирования необходимо составить четыре дополнительных уравнения. Они получаются из граничных условий и условий со-

вместности перемещений. Граничные условия: при z = 0, υ1 = 0; при z = ℓ, υ2 = 0

Условия совместности перемещений: при z = ℓ/2, φ1 = φ2 ; при z = ℓ/2, υ1 = υ2.

Подставив эти условия в уравнения системы (a) - (d) можно вычислить значения посто-

янных интегрирования. В данном примере задача облегчается в силу симметрии балки и нагрузки. Из уравнения (b) при z = 0 получаем D1 = 0. В середине балки поворот се-

чения равен нулю, поэтому при z = ℓ/2, φ1 = φ2 = 0, из (a) получаем С1 = - Рℓ2/16 ,

а из (с) С2 = - 3Рℓ2/16. Наконец из соотношения (d), учитывая, что z = ℓ,		υ2 = 0 полу-
чим D2 = Рℓ3/48. Таким образом, система уравнений для перемещений будет
(Е J) φ1	= (Е J) dυ1/dz = Рz2/4 - Рℓ2/16,	(11.19)
(Е J) υ1	= Рz3/12 - Рℓ2 z /16 ,	(11.20)
(Е J) φ2	= (Е J) dυ2/dz = - Рz2/4 + Рℓz/2 - 3Рℓ2/16,	(11.21)
(Е J) υ2	= - Рz3/12 + Рℓz2/4 - 3Рℓ2 z /16+ Рℓ3/48.	(11.22)

Для получения максимальных перемещений в середине пролета и угла поворота на опоре можно было ограничится вычислением только двух первых постоянных С1 и D1,

при z = 0, φ0 = - Рℓ2/(16 ЕJ); при z = ℓ/2, υmax = Рℓ3/(48 ЕJ).

9

Итак, если на различных участках балки изгибающий момент определяется раз-

личными аналитическими выражениями, необходимо составлять несколько дифферен-

циальных уравнения для определения перемещений и каждое уравнение должно соот-

ветствовать своему участку. Поэтому, число произвольных постоянных интегрирова-

ния должно быть равно удвоенному числу участков. Для их нахождения ставят усло-

вия совместности перемещений на границах участков, так как балка, деформируясь,

сохраняет непрерывность и гладкость своей оси. Условия совместности устанавливают,

что перемещение и угол поворота сечения на конце одного участка равны таким же ве-

личинам в начале следующего участка. Таким образом, каждая граница участков дает два условия совместности. Вместе с граничными условиями этого достаточно, чтобы составить замкнутую систему уравнений для определения произвольных постоянных интегрирования. Например, на рис. 11.6 представлена балка, для определения переме-

щений в которой, необходимо разбить ее на три участка. Это потребует определения шести произвольных постоянных интегрирования. На границах участков можно соста-

вить четыре уравнения совместности перемещений и на опорах балки еще два гранич-

ных условия (перемещения на опорах равны нулю). Таким образом, будет получена замкнутая система уравнений, из которой определятся все произвольные постоянные.

Рис. 11.6. Балки при действии системы нагрузок.

Заметим, что такой подход приводит к достаточно трудоемкой процедуре, поэтому ме-

тод непосредственного интегрирования дифференциальных уравнений применяется только в простых случаях, когда число участков с гладкой эпюрой моментов невелико.

10

Лекция 12

Теоремы о взаимности работ и перемещений. Определение линейных и угловых перемещений в балках по формуле Мора

Существует более простой способ вычисления перемещений в стержневых сис-

темах, чем метод прямого интегрирования дифференциальных уравнений. Для его вы-

вода необходимо предварительно познакомиться с некоторыми теоремами. Для про-

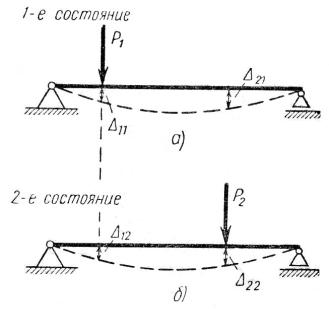
стоты, возьмем балку постоянного сечения, покоящуюся на двух опорах и рассмотрим ее в двух состояниях при загружении сосредоточенными силами, рис. 12.1. Под дейст-

вием этих сил балка деформируется, и приложенные внешние силы производят на сво-

их перемещениях некоторую работу. Введем следующие обозначения. Каждое переме-

щение, вызванное какой либо системой сил, будем обозначать греческой буквой i,j

с двумя индексами. Первый индекс будет обозначать состояние (место и направление перемещения), второй причину этого перемещения, т.е. состояние (воздействие) вслед-

ствие которого это перемещение возникло. Например, 11 это перемещение в первом состоянии (точке приложения силы Р1 по ее направлению) и от действия сил этого же состояния (той же силы Р1). Перемещение по направлению и в точке приложения силы

Р2 от действия силы Р1 (сил первого состояния) обозначим как		21. Соответственно
22 - перемещение по направлению силы Р2	от ее же действия, а	12 - перемещение в
точке приложения силы Р1 от действия Р2	(сил второго состояния).

Рис. 12.1. Возможные состояния однопролетной балки

Теперь загрузим балку сразу двумя внешними силами и определим производимую ими работу на вызванных нагрузкой перемещениях. Для этого воспользуемся принципом