Архив2 / курсач docx20 / kursach_mekhanika
.docxЗадание 1
Постоянный
вращающий момент
Мв
=
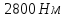 ,
приложенный
к ступенчатому блоку 2
силой
тяжести
,
приложенный
к ступенчатому блоку 2
силой
тяжести
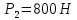 поднимает груз 1
силой
тяжести
поднимает груз 1
силой
тяжести
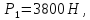 и приводит в движение ступенчатый каток
3
силой
тяжести
и приводит в движение ступенчатый каток
3
силой
тяжести посредством невесомых нерастяжимых
нитей. Радиусы блока 2
и
катка 3
соответственно
равны
посредством невесомых нерастяжимых
нитей. Радиусы блока 2
и
катка 3
соответственно
равны
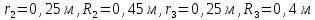 .
Радиусы
инерции блока 2
и
катка 3
относительно
осей
О
и O1
соответственно равны
.
Радиусы
инерции блока 2
и
катка 3
относительно
осей
О
и O1
соответственно равны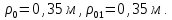 Скольжение
катка 3
по
наклонной плоскости и нитей о блок 2
отсутствует.
Участок нити
КС
параллелен плоскости, наклоненной к
горизонту под углом
ОС.
При расчетах принять
g
=
10 м/с2,
α =
30°. Определить
ускорение груза 1,
используя теорему
об изменении кинетической энергии.
Скольжение
катка 3
по
наклонной плоскости и нитей о блок 2
отсутствует.
Участок нити
КС
параллелен плоскости, наклоненной к
горизонту под углом
ОС.
При расчетах принять
g
=
10 м/с2,
α =
30°. Определить
ускорение груза 1,
используя теорему
об изменении кинетической энергии.
Рис.1
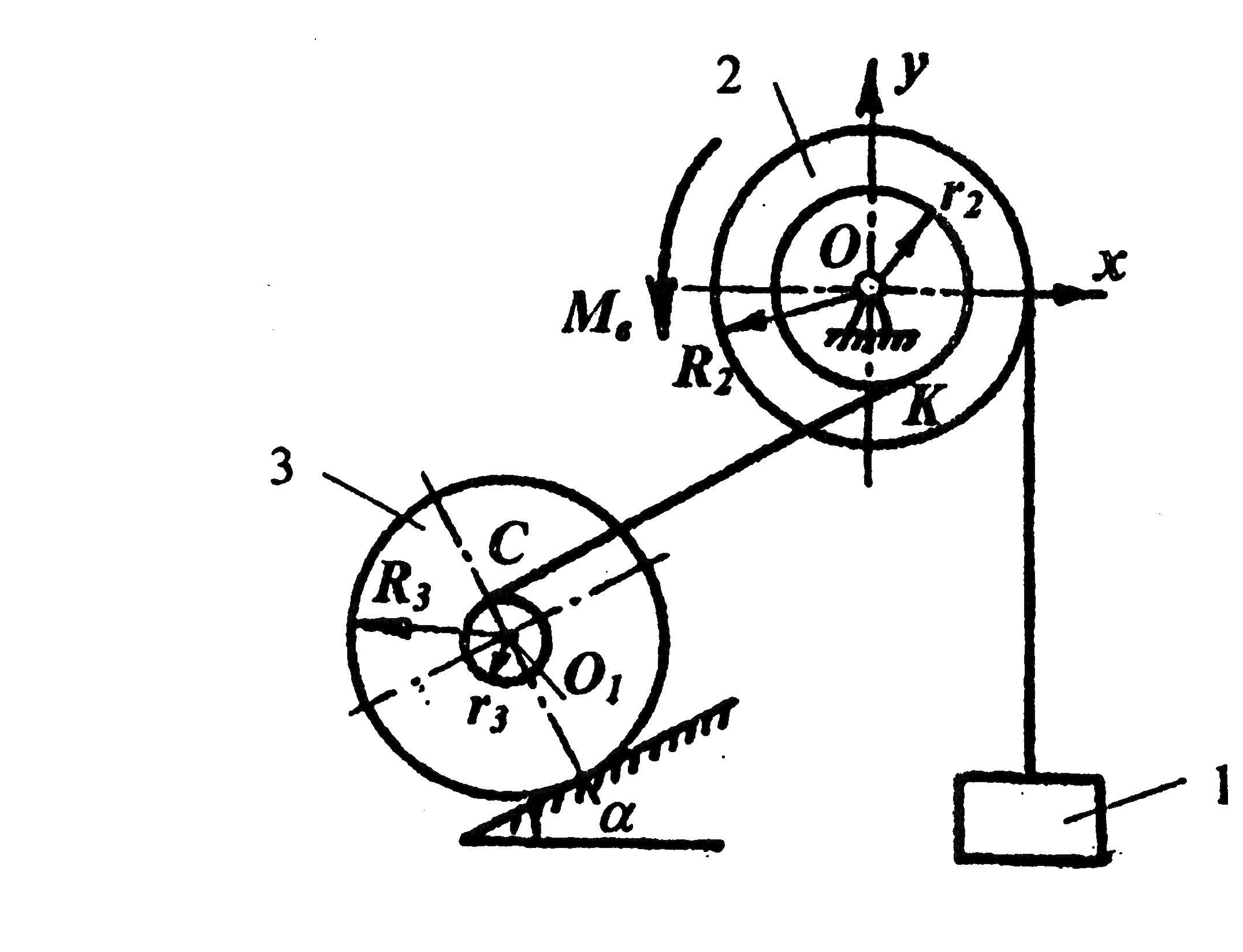
Решение. Применим теорему об изменении кинетической энергии системы:

где
Т0
и
Т —
кинетическая энергия системы в начальном
и конечном положениях;
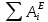 —
сумма работ внешних сил, приложенных к
системе;
—
сумма работ внешних сил, приложенных к
системе;
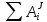 — сумма работ внутренних сил системы.
— сумма работ внутренних сил системы.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,
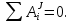
Так
как
в
начальном положении система находится
в покое, то
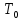 = 0.
= 0.
Следовательно, уравнение (1) принимает вид:
Кинетическая энергия рассматриваемой системы Т в конечном ее положении равна сумме кинетических энергий тел 1, 2, 3:
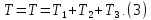
Покажем на рис.2 приложенные силы и направление перемещения каждого из элементов:

Кинетическая энергия груза 1, движущегося поступательно,
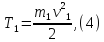
где
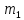 — масса груза 1
— масса груза 1
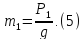
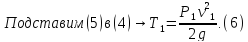
Кинетическая энергия блока 2, вращающегося вокруг неподвижной оси О,

где
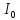 — момент инерции блока 2 относительно
оси О:
— момент инерции блока 2 относительно
оси О:
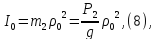
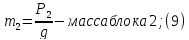
 — угловая
скорость блока 2:
— угловая
скорость блока 2:
Скорость точки А блока 2 равна скорости груза 1, тогда
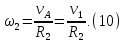
Подставляя (8)—(10) в формулу (7), получим
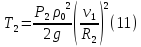
Кинетическая энергия катка 3, совершающего плоское движение,
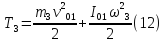
где
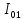 — момент инерции блока 3 относительно
оси О1:
— момент инерции блока 3 относительно
оси О1:
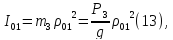

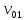 — скорость
центра тяжести
O1
блока 3.
— скорость
центра тяжести
O1
блока 3.
Cкорость точки К блока 2 равна скорости точки С блока 3:
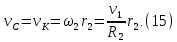
Так как каток катится без скольжения, то мгновенный центр скоростей катка находится в точке P. Поэтому
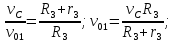
откуда после подстановки выражения (15) получаем
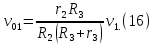
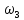 —
угловая
скорость блока
3
—
угловая
скорость блока
3
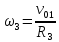
подставим в это выражение значение (16)
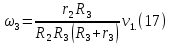
Подставляя (13), (14), (16), (17) в формулу (12), получаем

Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (6), (11), (18):
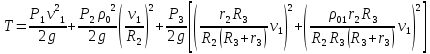
Подставляя сюда заданные значения, получаем
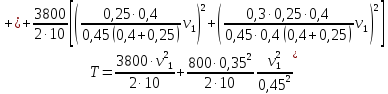
или
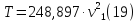
Найдем сумму работ всех внешних сил, приложенных к системе.
Работа силы тяжести P1
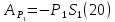
где
 перемещение груза 1.
перемещение груза 1.
Работа вращающего момента MB
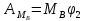
где
 угол поворота блока 2
угол поворота блока 2
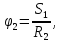
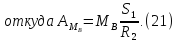
Работа силы тяжести P3
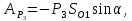
где
 перемещение блока 3.
перемещение блока 3.
Перемещения относятся между собой также, как скорости, потому
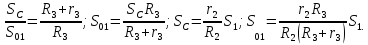
Тогда

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (20)—(22):
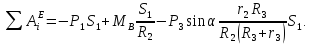
Подставляя заданные значения, получаем
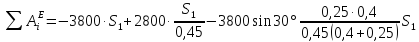
или
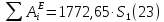
Согласно
теореме (2) приравняем значения
Т
и
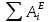 ,
определяемые по формулам (19) и (23):
,
определяемые по формулам (19) и (23):

откуда
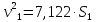
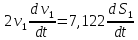
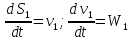
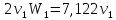
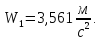
Задание 2
Решить задание 1 с помощью принципа Даламбера.
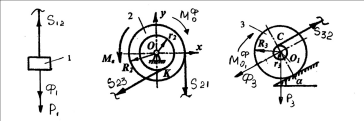
Рис.3
Решение. «Разделим» систему на три составляющие (рис.3) и обозначим приложенные силы, после чего для каждой из составляющих (груза 1, блоков 2 и 3) составим уравнение

где
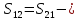 натяжение нити между блоком 2 и грузом
1;
натяжение нити между блоком 2 и грузом
1;
 натяжение
нити между блоком 2 и блоком 3;
натяжение
нити между блоком 2 и блоком 3;
 момент
инерции блока 2 относительно оси О;
момент
инерции блока 2 относительно оси О;
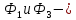 силы
инерции, приложенные к грузу 1 и блоку
3 соответственно.
силы
инерции, приложенные к грузу 1 и блоку
3 соответственно.
Так
как
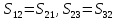 преобразуем
систему (24) к следующему виду:
преобразуем
систему (24) к следующему виду:
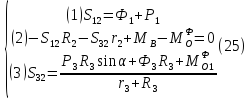
После
чего, подставив значения
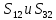 в уравнение (2) данной системы, выразим
значение скорости груза 1. Для этого
найдем значения неизвестных сил.
в уравнение (2) данной системы, выразим
значение скорости груза 1. Для этого
найдем значения неизвестных сил.
Груз
1.
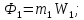 подставим сюда выражение (5), тогда
подставим сюда выражение (5), тогда
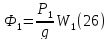
Блок
2.

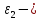 угловое
ускорение блока 2, так как ускорение
груза 1
угловое
ускорение блока 2, так как ускорение
груза 1
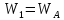 равно ускорению точки А блока 2 (рис.2),
равно ускорению точки А блока 2 (рис.2),
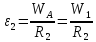 ;
;
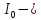 момент
инерции блока 2 относительно оси О:
момент
инерции блока 2 относительно оси О:
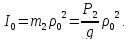 Тогда
Тогда
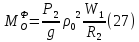
Блок
3.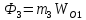 ,
где
,
где
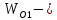 ускорение блока 3. Так как
ускорение блока 3. Так как
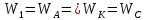 (рис.2), то
(рис.2), то
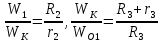
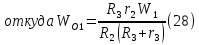
Тогда, подставив (28) и (14)
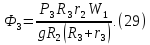
 где
где
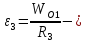 ускорение
блока 3,
ускорение
блока 3,
 — момент инерции блока 3 относительно
оси О1:
— момент инерции блока 3 относительно
оси О1:
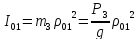 .
Подставим эти выражения и (28), тогда
.
Подставим эти выражения и (28), тогда
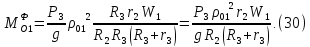
Подставим в систему (24) значения выражений (25) – (27), (29) – (30)
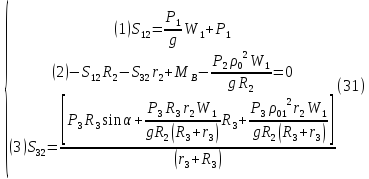
Подставим уравнения (1) и (3) в уравнение (2) этой системы
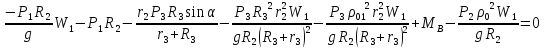
Выразим
отсюда
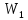
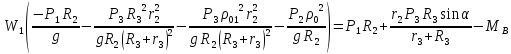
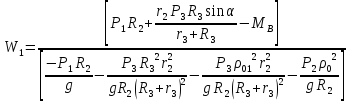
Подставим в это выражение числовые значения, и найдем скорость груза 1

или
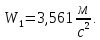
Задание 3
Решить задание 1 с помощью уравнения Лагранжа 2-ого рода.
Решение.
Воспользуемся уравнением Лагранжа
второго рода. Приняв за обобщенную
координату системы, имеющей одну степень
свободы, перемещение груза 1 –
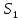 ,
имеем:
,
имеем:

Кинетическая энергия рассматриваемой системы Т в конечном ее положении равна сумме кинетических энергий тел 1, 2, 3:
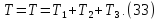
Покажем на рис.4 приложенные силы и направление перемещения каждого из элементов:
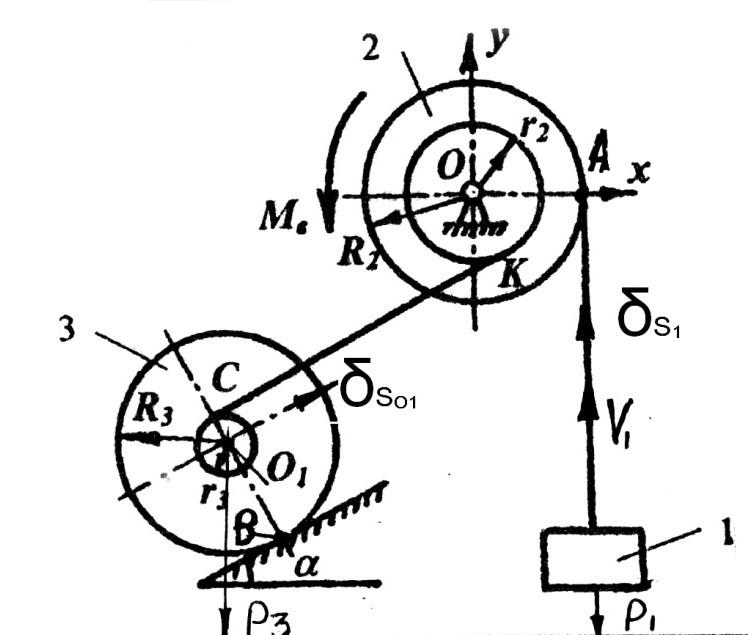
Рис.4
Кинетическая энергия груза 1, движущегося поступательно,

где
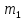 — масса груза 1
— масса груза 1
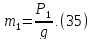
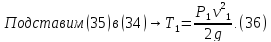
Кинетическая энергия блока 2, вращающегося вокруг неподвижной оси О,
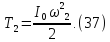
где
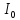 — момент инерции блока 2 относительно
оси О:
— момент инерции блока 2 относительно
оси О:
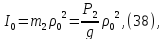
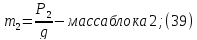
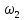 — угловая
скорость блока 2:
— угловая
скорость блока 2:
Скорость точки А блока 2 равна скорости груза 1, тогда
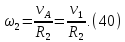
Подставляя (38)—(40) в формулу (7), получим
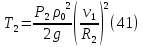
Кинетическая энергия катка 3, совершающего плоское движение,

где
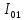 — момент инерции блока 3 относительно
оси О1:
— момент инерции блока 3 относительно
оси О1:

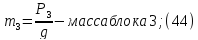
 — скорость
центра тяжести
O1
блока 3.
— скорость
центра тяжести
O1
блока 3.
Cкорость точки К блока 2 равна скорости точки С блока 3:

Так как каток катится без скольжения, то мгновенный центр скоростей катка находится в точке P. Поэтому
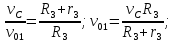
откуда после подстановки выражения (45) получаем
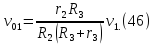
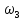 —
угловая
скорость блока
3
—
угловая
скорость блока
3

подставим в это выражение значение (46)
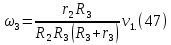
Подставляя (43), (44), (46), (47) в формулу (42), получаем
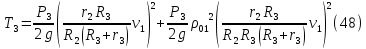
Кинетическая энергия всей механической системы определяется по формуле (33) с учетом (36), (41), (48):
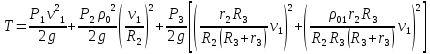
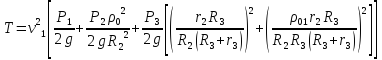
или,
так как
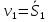

Найдем
обобщенную силу
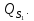 Сообщим
перемещению
Сообщим
перемещению
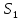 приращение
приращение
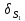 и составим сумму элементарных работ
задаваемых сил на этом возможном
перемещении. В эту сумму войдет работа
вращающего момента
МВ
и работа сил тяжести,
которая отрицательна.
и составим сумму элементарных работ
задаваемых сил на этом возможном
перемещении. В эту сумму войдет работа
вращающего момента
МВ
и работа сил тяжести,
которая отрицательна.
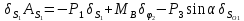


Тогда
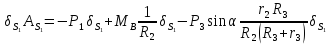
Обобщенная сила

Найдем значения членов левой части уравнения (32):

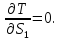
Уравнение (32) примет вид
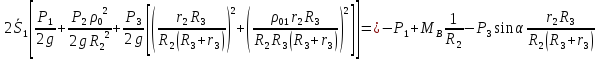
Тогда
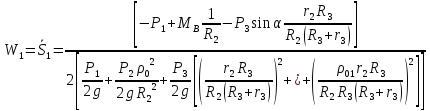
Подставляя в эту формулы заданные числовые значения всех величин, находим:

или
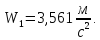
Задание 4
Определить частоту и период малых свободных колебаний механической системы с одной степенью свободы, пренебрегая силами сопротивления и массами нитей.
Найти
уравнение движения груза 1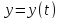 ,
приняв за начало отсчета положение
покоя груза 1 (при статической деформации
пружин). Найти также амплитуду
колебаний груза 1.
,
приняв за начало отсчета положение
покоя груза 1 (при статической деформации
пружин). Найти также амплитуду
колебаний груза 1.
В
задании приняты следующие обозначения:
1 — груз массой
т1,
2 —
блок массой т2
и радиусом
r2
(сплошной однородный диск); 4
—
сплошной однородный диск массой
т4
и радиусом
r4;
6 —тонкий однородный стержень массой
т6
и длиной l;
7 —стержень, масса которого не учитывается;
с
—коэффициент жесткости пружины; у0
— начальное отклонение груза 1 по
вертикали от положения покоя,
соответствующего статической деформации
пружины;
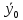 —
проекция начальной скорости
—
проекция начальной скорости
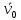 груза 1 на вертикальную ось (рис.5).
груза 1 на вертикальную ось (рис.5).
Дано:

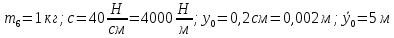 /с=
0,005 м/с. (рис.5)
/с=
0,005 м/с. (рис.5)
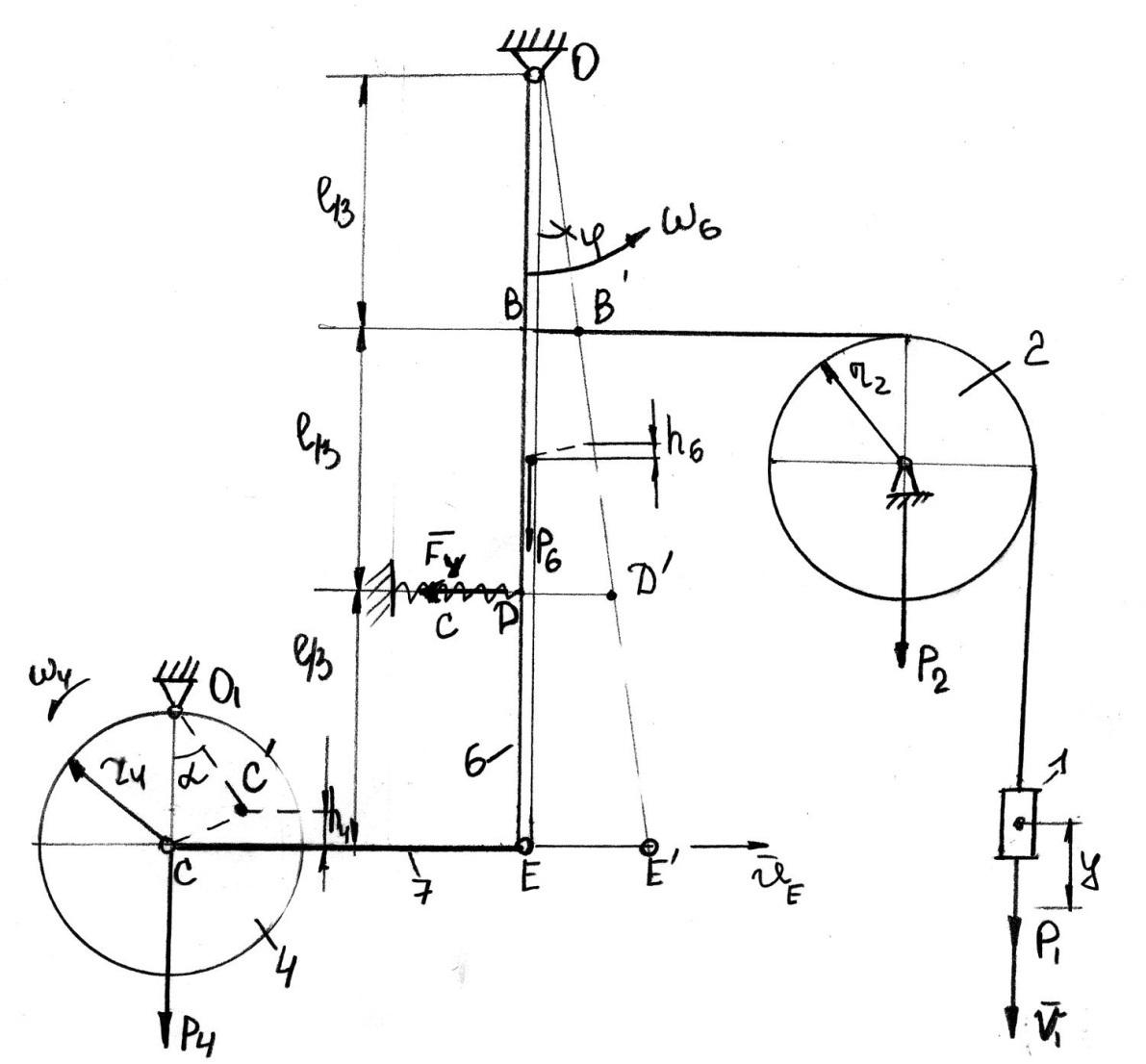
Рис.5
Решение. Воспользуемся уравнением Лагранжа второго рода для консервативной системы. Приняв за обобщенную координату вертикальное отклонение y груза 1 от положения покоя, соответствующего статической деформации пружины, имеем

где Т — кинетическая энергия системы; П — потенциальная энергия системы.
Кинетическую энергию Т вычислим с точностью до величин второго порядка малости относительно обобщенной скорости у, а потенциальную энергию П — с точностью до величии второго порядка малости относительно обобщенной координаты у.
Найдем кинетическою энергию системы, равную сумме кинетических энергий тел 1,2, 4, и 6:

выразив
линейные и угловые скорости, которыми
определяется кинетическая энергия тел
этой системы, через обобщенную скорость
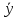 .
.
Кинетическая
энергия груза 1, движущегося поступательно
со скоростью


Кинетическая энергия блока 2 (сплошного однородного диска):
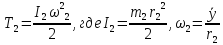
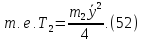
Кинетическая энергия тонкого однородного стержня 6:
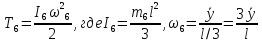
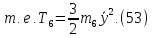
Кинетическая энергия сплошного однородного диска 4
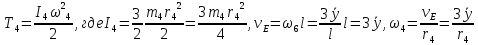
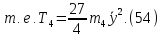
Таким образом, кинетическую энергию рассматриваемой механической системы получим, подставив в формулу (7) значения выражений (51)-(54)
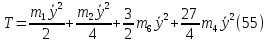
Найдем потенциальную энергию системы
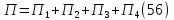
Работа
сил тяжести при перемещении груза 1 из
координаты
 в нулевое положение
в нулевое положение

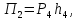 где
где
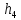 – вертикальное перемещение центра
тяжести колеса 4
– вертикальное перемещение центра
тяжести колеса 4

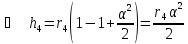

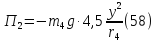
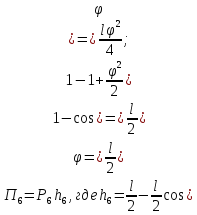
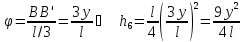
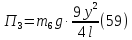
Потенциальная энергия деформированной пружины при указанном перемещении системы
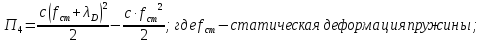
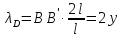 – перемещение
точки D
– перемещение
точки D

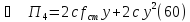
Найдем полную потенциальную энергию системы, подставив в формулу (56) значения выражений (57)-(60)

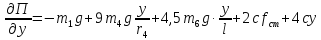
В состоянии покоя, y=0

следовательно, потенциальная энергия рассматриваемой механическо й системы
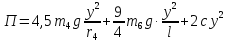
Найдем значения членов уравнение (49):

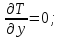
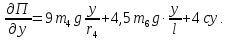
Подставив эти данные в уравнение (49), получим
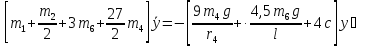
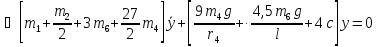
Обозначив
через
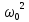 коэффициент
при
коэффициент
при
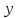 ,
имеем
,
имеем
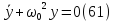
Циклическая частота свободных колебаний
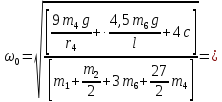
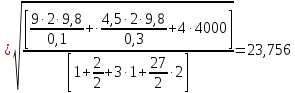
Период свободных колебаний
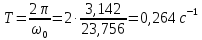
Интегрируя уравнение (61), получим уравнение движения груза 1
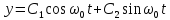
Для
определения постоянных
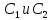 найдем уравнение скорости груза
найдем уравнение скорости груза
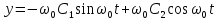
и воспользуемся начальными условиями задачи
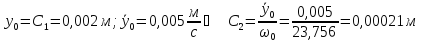
Подставляем
значения постоянных в уравнение
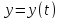

Уравнение
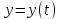 можно получить в другом виде, если
перейти к другим постоянным интегрирования
a
и β,
приняв
можно получить в другом виде, если
перейти к другим постоянным интегрирования
a
и β,
приняв

Тогда
 ,
,
где

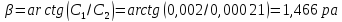
Окончательно,