Методические рекомендации к изучению тем курса и выполнению контрольных работ

Тема 1. Элементы линейной алгебры

Матрицы. Действия над матрицами. [3, §1]. Определители. Свойства определителей. [3, §2]. Невырожденные матрицы. Обратная матрица. [3, §3]. Ранг матрицы. [3, §3]. Системы линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений по правилу Крамера,с помощью обратной матрицы,методом Гаусса. [3, §4].

Пример 1. Дана матрица . Найти.

Решение: Транспонируем матрицу :. Матрицаимеет размерность, матрицаимеет размерность. Значит, произведение этих матриц возможно, и матрицабудет иметь размерность.

.

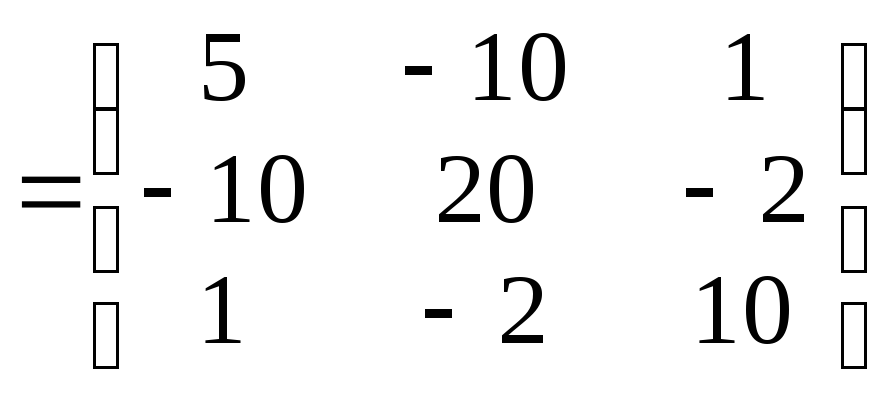Определитель матрицы найдем, воспользовавшись «правилом треугольников»:

Пример 2. Решить систему уравнений 1) по правилу Крамера; 2) с помощью обратной матрицы; 3) методом Гаусса.

Решение: 1. Найдем главный определитель системы:

Так как , то система имеет единственное решение.

Найдем вспомогательные определители системы:

; ;.

Значит, ;;.

2. Запишем заданную систему уравнений в матричной форме , где– матрица коэффициентов системы;– столбец неизвестных;– столбец свободных членов.

Тогда , где– обратная матрица к матрице.

Так как , тосуществует. Обратная матрицаможет быть найдена по формулегде– алгебраическое дополнение элементаматрицы;– минор элементаматрицы, то есть определитель, полученный из матрицыпутем вычеркивания-й строки и-го столбца.

Определитель второго порядка может быть найден по формуле .

Находим алгебраические дополнения элементов матрицы :

; ;.

Аналогично ;;;;;.

Значит, .

Тогда

,

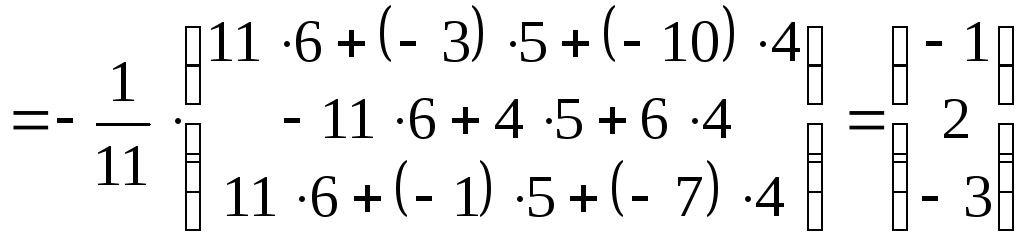то есть ,,.

3. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду:

.

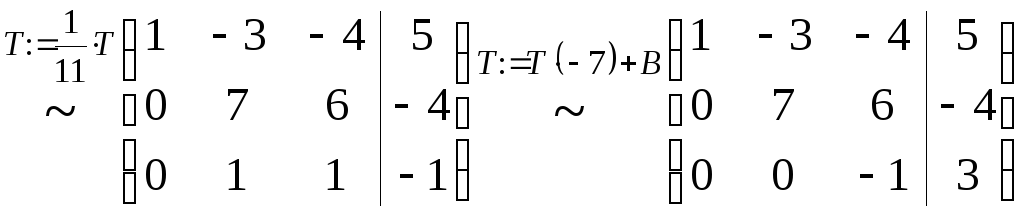Откуда следует, что ранги матриц иравны, то есть система уравнений совместна. Число неизвестных, значит, система уравнений имеет единственное решение.

Перейдем от полученной ступенчатой матрицы к системе, эквивалентной заданной:

Решая систему «снизу вверх», получаем, что ,,.

Тема 2. Элементы векторной алгебры

Векторы. Линейные операции над векторами. Проекция вектора на ось. Модуль вектора. Направляющие косинусы. [3, §5]. Скалярное произведение векторов. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Некоторые приложения скалярного произведения. [3, §6]. Векторное произведение векторов. Свойства векторного произведения. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения. [3, §7]. Смешанное произведение векторов. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Некоторые приложения смешанного произведения. [3, §8]. Собственные векторы и собственные значения матриц. [4, гл. V, §4].

Пример 3. Дано: ,, векторыисоставляют стороны параллелограмма. Найти: 1) длины диагоналей параллелограмма; 2) острый угол между диагоналями параллелограмма; 3) площадь параллелограмма.

Решение: Сделаем схематический чертеж:

1. Найдем длины диагоналей параллелограмма как длины векторови.

Скалярный квадрат вектора равен квадрату модуля этого вектора, то есть и. Имеем

.

2. Острый угол между диагоналями параллелограмма найдем по формуле.

Находим скалярное произведение векторов и:

Значит, и.

3. Площадь параллелограмма найдем по формуле.

По свойствам векторного произведения имеем

Значит,

Пример 4. Даны точки ;;;. Требуется: 1) записать векторы,,в ортонормированном базисе; 2) найти длины векторов,,; 3) показать, что векторы,,образуют базис трехмерного пространства; 4) найти острый угол между векторамии; 5) найти алгебраическую проекцию векторана вектор; 6) найти площадь треугольника; 7) найти объем пирамиды.

Решение: 1. Если ,, то вектор.

В данном случае имеем .

Значит, ,,.

2. Длина вектора может быть найдена по формуле.

Имеем ;;

.

3. Покажем, что векторы ,,образуют базис трехмерного пространства. Для этого найдем определитель, составленный из координат этих векторов:

Так как , то векторы,,образуют базис трехмерного пространства.

4. Острый угол между векторами инайдем по формуле.

Скалярное произведение векторов инайдем, используя формулу:, где,. В данном случае.

Тогда и.

5. Алгебраическую проекцию вектора на векторнайдем по формуле.

Так как , то.

6. Площадь треугольника найдем по формуле.

Векторное произведение векторов иможно найти по формуле.

В данном случае

Тогда ,. Значит,.

7. Объем пирамиды найдем по формуле.

Смешанное произведение векторов ,иможно найти по формуле.

Тогда . Значит,.

Пример 5. Найти собственные значения и собственные векторы матрицы .

Решение: Собственные значения матрицы находятся из уравнения, где– единичная матрица того же порядка, что и матрица.

В данном случае ,

.

Решением уравнения являются числа,. Это и есть собственные значения матрицы.

Собственный вектор , соответствующий собственному значению, определяется из системы уравнений.

Находим собственный вектор , отвечающий собственному значению:или. Пусть, тогда.

Значит, – собственный вектор, соответствующий собственному значению.

Находим собственный вектор , отвечающий собственному значению:или. Пусть, тогда.

Значит, – собственный вектор, соответствующий собственному значению.