
- •Идея метода гаусса
- •Уравнение плоскости орбиты светила
- •Отношения площадей треугольников
- •Исправление моментов времени за планетную аберрацию
- •1 А.Е. Свет пройдет за (499.0s или 8m19.0s).
- •Вычисление отношения площади сектора к площади треугольника
- •Второе и дальнейшие приближения
- •Определение элементов орбиты
- •Алгоритм вычислений
- •Формула эйлера
Отношения площадей треугольников
Предположим
для простоты, что плоскость координат
![]() совпадает с плоскостью орбиты светила.
Тогда уравнения движения примут вид
совпадает с плоскостью орбиты светила.
Тогда уравнения движения примут вид
 [15]
[15]
![]() -
масса светила пренебрежимо мала по
сравнению с массой Солнца. Выберем
единицу измерения времени так, чтобы
-
масса светила пренебрежимо мала по
сравнению с массой Солнца. Выберем
единицу измерения времени так, чтобы
![]() .
Масса и расстояние измеряются в массах
Солнца и астр. единицах соответственно,
можно подобрать лишь единицу измерения
времени, входящего в
.
Масса и расстояние измеряются в массах
Солнца и астр. единицах соответственно,
можно подобрать лишь единицу измерения
времени, входящего в
![]() :
:
![]() .
.
Здесь
время измеряется в сутках, исходя из
размерности
![]() ,
время
,
время
![]() измеренное в новых единицах, связано с
временем, измеренным в средних сутках
измеренное в новых единицах, связано с
временем, измеренным в средних сутках
![]() .
.
![]() средних суток.
средних суток.
Теперь
вместо времени t вводим
новую переменную
![]() . [16]
. [16]
Уравнения [15] заменяются следующими
 [17]
[17]
Пусть
в исходный момент времени, когда
![]() ,
светило имеет координаты
,
светило имеет координаты
![]() и радиус-вектор r;
и радиус-вектор r;
в
момент
![]() ,
соответственно -
,
соответственно -
![]() .
.

Требуется определить площадь треугольника, считая известным r и его производные по времени.
Допустим
![]() ,
тогда можно представить
,
тогда можно представить
![]()
![]() [18]
[18]
Дифференцируя
[17] по
![]() ,
можно получить выражение высших
производных
,
можно получить выражение высших
производных
![]() ,
содержащие только
,
содержащие только
![]() ;
;
![]() :
:
 [19]
[19]
Подставляя эти производные в [18]:
![]()
![]()
или
 [20]
[20]
где
 [21]
[21]
Выражения
[20] связывают координаты светила в момент
![]() с его координатами в момент
с его координатами в момент
![]() .
Из [20] можно определить искомую удвоенную
площадь треугольника:
.
Из [20] можно определить искомую удвоенную
площадь треугольника:
![]() [22]
[22]
Скобка справа это удвоенная секторная скорость, которая сохраняется при движении. При рассмотрении задачи двух тел был получен интеграл секторной скорости (закон сохранения момента импульса - [37]):
![]() .
.
В
рассматриваемом случае
![]() (орбита лежит в координатной плоскости),
(орбита лежит в координатной плоскости),
![]() :
:
![]() [23]
[23]
Применим
этот результат к трем положениям светила
и найдем удвоенные площади треугольников
![]() .
Промежутки времени обозначим
.
Промежутки времени обозначим
 [24]
[24]
причем
индекс у
![]() соответствует индексу, недостающему
справа (заметим, что
соответствует индексу, недостающему
справа (заметим, что
![]() ).
).
В
[20] полагаем
![]() ;
и заменяя
;
и заменяя
![]() соответственно на
соответственно на
![]() ;
;
![]() :
:

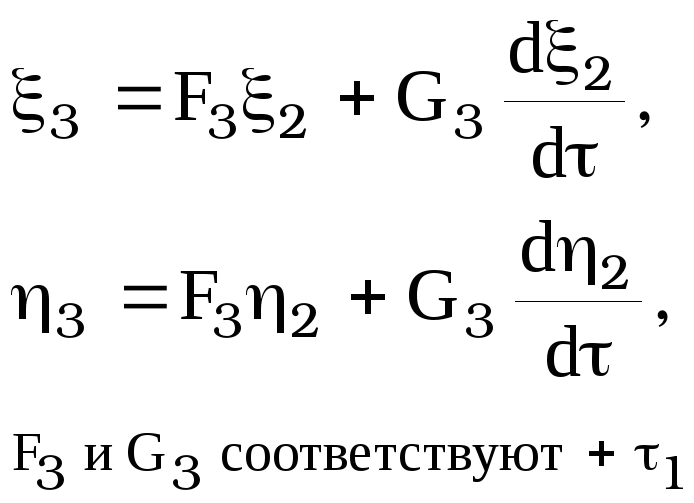 [25]
[25]
(исходя из положения 2, хотим получить положение 1, значит «-», см.[24])
(исходя из положения 2, хотим получить положение 3, значит «+», см.[24])
 [26]
[26]
Итак


![]()
![]()
![]()
![]()
![]()
Продолжим 

 .
.
Следовательно, удвоенные площади треугольников определяются:
 [27]
[27]
где
в последнем равенстве использовано
![]() .
.
Площади
треугольников выражены через
![]() и промежутки времени, но
и промежутки времени, но
![]() пока неизвестно.
пока неизвестно.

Итак,
 ,
,
Аналогично  .
.
Эти формулы даны Энке и они точнее тех, которыми пользовался сам Гаусс. Положим
 [28]
[28]
Тогда
![]() [29]
[29]
Вспомним [13] и [14]:
![]() подставим
сюда
подставим
сюда
![]() :
:
![]()
или ![]() [30]
[30]
где ![]() [31]
[31]
Тем
самым
![]() выразилось не через две неизвестные
выразилось не через две неизвестные
![]() (см. [13]), а через одну неизвестную
(см. [13]), а через одну неизвестную
![]() .
.
Н о
между
о
между
![]() и
и
![]() существует, кроме того, очень простое
геометрическое соотношение, вытекающее
из треугольника Солнце-Земля-светило.
существует, кроме того, очень простое
геометрическое соотношение, вытекающее
из треугольника Солнце-Земля-светило.
Напомним,
что
![]() - геоцентрические координаты Солнца.
- геоцентрические координаты Солнца.
Направляющие
косинусы
![]() известны из наблюдений
известны из наблюдений
![]() см. формулы [10].
см. формулы [10].
Скалярное произведение
![]() . [32]
. [32]
Применим теорему косинусов
![]() , [33]
, [33]
из
[32] известно
![]() .
.
Итак, имеем систему двух уравнений [30] и [33] с двумя неизвестными:
 [34]
[34]
Эту
систему можно решать методом
последовательных приближений относительно
![]() (аналитически не удается).
(аналитически не удается).
В
1-м приближении
![]() (см.[30]),
(см.[30]),
это
![]() (т.е.
(т.е.
![]() )
подставляем во 2-е уравнение [34],
)
подставляем во 2-е уравнение [34],
получаем
![]() ,
,
это
![]() подставляем в 1-е уравнение [34],
подставляем в 1-е уравнение [34],
и
получаем новое
![]() .
.
2-е
приближение
![]() и т.д.
и т.д.
Процесс итераций продолжается до совпадения 4-х значащих цифр в двух последовательных приближениях.
Итак,
найдены
![]() и
и
![]() ,
и значит по формулам [29] можно получить
отношения площадей треугольников
,
и значит по формулам [29] можно получить
отношения площадей треугольников
![]() .
.
1-е ПРИБЛИЖЕНИЕ ДЛЯ КООРДИНАТ СВЕТИЛА
Отношения
площадей треугольников
![]() получены в 1-м приближении. Обратимся к
системе уравнений [12]
получены в 1-м приближении. Обратимся к
системе уравнений [12]
 [12]
[12]
Зная
правые части, решаем систему относительно
неизвестных
![]() .
Далее получаем
.
Далее получаем
![]() .
.
![]() ,
полученное из системы [12], полезно
сравнить с
,
полученное из системы [12], полезно
сравнить с
![]() ,
полученным из системы [11]; это контроль
вычислений.
,
полученным из системы [11]; это контроль
вычислений.
Теперь из системы [11] получаем 1-е приближение гелиоцентрических координат светила:


![]()

![]() -
контроль вычислений (сравнить с решением
[34]).
-
контроль вычислений (сравнить с решением
[34]).
Контроль вычислений с использованием системы [9]:

Дополнительный контроль вычислений:
 где
где
![]()
Если
контроль показывает правильность
вычислений, то гелиоцентрические
координаты светила, таким образом,
получены в первом приближении для трех
моментов наблюдения. Вычисления здесь
носили приближенный характер, так как
при вычислении
![]() (формулы [29]) были отброшены члены высших
порядков в рядах разложения.
(формулы [29]) были отброшены члены высших
порядков в рядах разложения.
