1.1.2. Метод последовательных приближений

Рассмотрим задачу Коши для дифференциального уравнения первого порядка с начальным условием.

Метод последовательных приближений состоит в том, что решение , получают как предел последовательности функций, которые находятся по рекурсивной формуле

. (1.4)

Если правая часть в некотором замкнутом прямоугольнике, содержащем множество точек, для которых выполняются условияудовлетворяет условию Липшица по:

,

то независимо от выбора начальной функции последовательные приближения сходятся на некотором отрезкек точному решению задачи Коши.

Если непрерывна в области, то оценка погрешности приближенного решения на отрезке дается неравенством:

, (1.5)

где , а число определяется из условия:

.

Пример 1.1. Найти три последовательных приближения решения уравнения:

с начальным условием Оценить погрешность третьего приближения на отрезке.

Решение. Учитывая начальное условие, заменим уравнение интегральным

.

В качестве начального приближения возьмем . Первое приближение находим по формуле (1.4):

.

Аналогично получаем второе и третье приближения:

,

Оценим погрешность последнего приближения по формуле (1.5). Так как функция , то она определена и непрерывна во всей плоскостии в качествеиможно взять любые числа. Возьмем для определенности. При таких ограничениях получаем:

,

.

Таким образом, на отрезке [0; 0.4] получаем

,

и, следовательно:

.

Замечание: Оценка погрешности по формуле (1.5) часто оказывается завышенной. Практически, применяя метод последовательных приближений, вычисления продолжают до такого при котором значениясовпадают в пределах допустимой точности.

Пример 1.2. Дана система

с начальными условиями Методом последовательных приближений найти решение этой системы на отрезке [0; 0,3] с точностью до.

Решение: Записываем систему в интегральной форме:

,

используя начальные значения, из системы находим ,. В качестве начальных приближений выберем:

,

При выборе начальных приближений используем первые два члена разложения функций в окрестности точки

Вычислим следующие приближения и:

,

.

Аналогично получаем:

,

.

Оценим разности ина отрезке [0; 0.3]:

,

Эти разности находятся в пределах заданной точности, причем члены, содержащие , малы на отрезке [0; 0,3]. Следовательно, с заданной точностью можно положить

,  .

1.1.3. Метод Эйлера

Рассмотрим дифференциальное уравнение с начальным условием.

Выбрав достаточно малый шаг , построим систему равноотстоящих узлов, ().

Приближенные значения по методу Эйлера вычисляются последовательно по формулам:

()

При оценке погрешности обычно используется двойной пересчет.

Если – вычисленное значениес шагом, а– соответствующее узловое значение, полученное с шагомh, то для ориентировочной оценки погрешности последнего значения можно использовать формулу:

Пример 1.3. Применяя метод Эйлера, составить на отрезке [0,1] таблицу значений решения уравнения:

с начальным условием , выбрав шаг.

Решение дифференциального уравнения приведено в таблице 1.1.

Таблица 1.1

Приближенное решение уравнения примера 1.3 методом Эйлера

№ шага				Точное решение
0	0	1,0000	0,2000	1,0000
1	0,2	1,2000	0,1733	1,1832
2	0,4	1,3733	0,1561	1,3416
3	0,6	1,5294	0,1492	1,4832
4	0,8	1,6786	0,1451	1,6124
5	1,0	1,8237		1,7320

Рассмотрим пример вычисления :

.

Для остальных значений вычисления проводятся аналогично.

1.1.4. Метод Эйлера–Коши

Метод Эйлера–Коши является модификацией метода Эйлера. Вычисления табличных значений решения и оценка погрешности проводятся по следующим формулам.

,

,

,

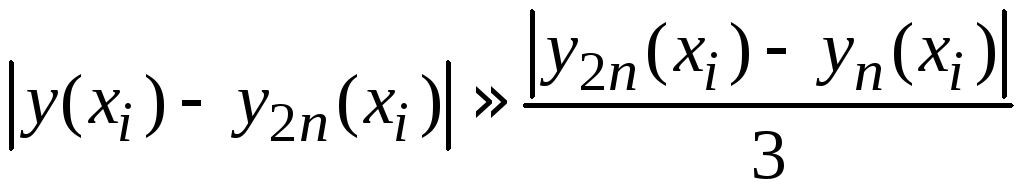где – точное значение решения в узле,,– приближенные значения решения в узлес шагом– соответственно.

Таблица 1.2

Приближенное решение уравнения примера 1.3 методом Эйлера–Коши

№ шага				Точное решение
0	0	1,0000	0,1867	1,0000
1	0,2	1,1867	0,1617	1,1832
2	0,4	1,3484	0,1454	1,3416
3	0,6	1,4938	0,1341	1,4832
4	0,8	1,6272	0,1263	1,6124
5	1,0	1,7542		1,7320

Рассмотрим применение метода Эйлера–Коши для примера 1.3, решенного выше методом Эйлера.

Покажем пример вычисления :

, .

Остальные значения проводятся аналогично. Результаты счета приведены в таблице 1.2.

1.1.5. Метод Рунге–Кутта четвертого порядка

Рассмотрим метод Рунге–Кутта четвёртого порядка для нахождения численного решения уравнения (1.1) с начальным условием (1.2).

Пусть является начальным условием (при), либо получено как результат предыдущего шага. Для получения следующего значениявначале вычисляются числа:

, (1.6)

где h– шаг интегрирования.

Затем вычисляют: .

Новое значение функции вычисляется по формуле:

. (1.7)

Метод Рунге–Кутта четвертого порядка является методом повышенной точности. На практике для контроля точности этого метода используется двойной счет пересчет.

Если – вычисленное значениес шагом, а– соответствующее узловое значение, полученное с шагомh, то для приближенной оценки погрешности значенияможно использовать формулу:

.

Пример 1.4. Решить методом Рунге–Кутта уравнение на отрезке [0, 1] с шагом h = 0,2:

.

Результаты вычислений оформим в виде таблицы 1.3.

Таблица 1.3

Результаты приближенного решения примера 1.4 методом Рунге–Кутта

четвертого порядка

0	0,0	1,0000	0,2000	0,1980	0,2000	0,1916	0,1972
1	0,2	1,1972	0,1916	0,1810	0,4000	0,1653	0,1799
2	0,4	1,3771	0,1653	0,1460	0,6000	0,1218	0,1448
3	0,6	1,5219	0,1217	0,0950	0,8000	0,0646	0,0941
4	0,8	1,6160	0,0646	0,0330	1,0000	0,0000	0,0326
5	1,0	1,6486

Покажем пример вычисления табличного значения .

Для вычисления надо вычислить:

Остальные значения вычисляются аналогично.