Rogers Computational Chemistry Using the PC

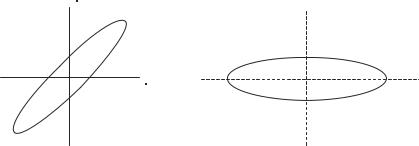
APPLICATIONS OF MATRIX ALGEBRA

43

y

x

Figure 2-1 A Particle on an Elliptical Orbit.

In general, the equation describing an elliptical path

ax2 þ 2bxy þ cy2 ¼ Q

contains mixed terms, 2bxy. For example, the equation of the ellipse on the left in Fig. 2-1 might look something like

5x2 þ 8xy þ 5y2 ¼ 9

ð2-40Þ

If we can find the appropriate X matrix to carry out a similarity transformation on the coefficient matrix for the quadratic equation (2-40)

A ¼	b	c	¼	4	5	ð2-41Þ
	a	b		5	4

we get

A0 ¼	1	0	ð2-42Þ
	0	9

which leads to the equation of the ellipse as represented on the right of Fig. 2-1

x02 þ 9y02 ¼ 9

ð2-43Þ

It turns out that the ‘‘appropriate X matrix’’ of the eigenvectors of A rotates the axes p/4 so that they coincide with the principle axes of the ellipse. The ellipse itself is unchanged, but in the new coordinate system the equation no longer has a mixed term. The matrix A has been diagonalized. Choice of the coordinate system has no influence on the physics of the situation, so we choose the simple coordinate system in preference to the complicated one.

The physical meaning of the sections on transformation matrices and unitary matrices is that we can try to rotate our coordinate system so that each component

44	COMPUTATIONAL CHEMISTRY USING THE PC

of the motion is independent of all the rest. We may be successful or nearly successful. Note well that there is no restriction on the number of dimensions of the n-dimensional space the coordinate system spans. When, in future work, we seek to diagonalize an n-dimensional matrix, we are seeking to rotate a set of orthonormal axes, one in each dimension of an n-space, such that each axis is a principal axis of the matrix.

The unitary transform does the same thing as a similarity transform, except that it operates in a complex space rather than a real space. Thinking in terms of an added imaginary dimension for each real dimension, the space of the unitary matrix is a 2m-dimensional space. The unitary transform is introduced here because atomic or molecular wave functions may be complex.

PROBLEMS

1. Carry out hand calculations to find the products AB and BA

A ¼	0 4		1 1 1			B ¼	0 2		1	6 1
	@	3	0	3	A		@	1	1	1
		1	2	5				3	4	5 A

Do A and B commute?

2.Write a program in BASIC to carry out the multiplications in Problem 1. Crosscheck your program results with your hand calculations from Problem 1.

3.Invert A in Problem 1. Systematic methods exist for inverting matrices and will be discussed in the next chapter. For now, use Mathcad if it is available to you.

4.Find AA 1. Is it true that AA 1 ¼ I? Does A commute with A 1?

5.Transpose A and B in Problem 1.

6.Transpose the product AB to find ðABÞT.

7.Find the product ATBT; compare it with the transpose of the product from Problem 6. Deduce a rule for ATBT.

8.Is the matrix Q conformable to multiplication into its own transpose? What about QTQ? What is the dimension of QQT? What is the dimension of QTQ?

0 1

pq

Q ¼ @ r s A

tu

9.The problem of a mass suspended by a spring from another mass suspended by another spring, attached to a stationary point (Kreyszig, 1989, p. 159ff) yields the matrix equation

Ax ¼ lx

where x is a vector. For a certain combination of masses and springs,

A ¼	5	3
	3	5

APPLICATIONS OF MATRIX ALGEBRA

45

Is l ¼ 7 an eigenvalue of the system? Is l ¼ 8 an eigenvalue of the system? There is another eigenvalue. What is it?

10. The transpose of xy is ð x y Þ. Carry out the multiplication

ð x y Þ	5	4	x
	4	5	y

11.The eigenvector matrix for a p=4 rotation is

1		1	1
X ¼ p2		1	1

Carry out the rotation

	X	T 5	4	X
		4	5

Linear Nonhomogeneous Simultaneous Equations

The problem of n linear independent nonhomogeneous equations in n real unknowns

a11x1 þ a12x2 ¼ b1

ð2-44Þ

a21x1 þ a22x2 ¼ b2

is often encountered in an experimental context. We have taken two equations in two unknowns for notational simplicity, but the equation set may be extended to the n-variable case. Many coded programs have been published in FORTRAN (e.g., Carnahan and Luther, 1969; Isenhour and Jurs, 1979) for each of the algorithms discussed here. Most are short and easily translated into other computer languages. The problem of more than n equations in n real unknowns is called the multivariate problem. Linearly dependent homogeneous equations frequently occur in some branches of quantum mechanics. These problems will be treated later.

Linear independence implies that no equation in the set can be obtained by multiplying any other equation in the set by a constant. The n n matrix populated by n2 elements aij

A ¼	a11	a12	ð2-45Þ
	a21	a22

is called the coefficient matrix. For the set to be linearly independent, the rank of A must be n. An ordered set of numbers is a vector; hence the ordered number pair

x ¼ x1 is called the solution vector or solution set and the ordered set of constants

x2

b2

b1

46	COMPUTATIONAL CHEMISTRY USING THE PC

b ¼ is called the constant vector. I like the term nonhomogeneous vector, because existence of any nonzero element bi causes the equation set to be nonhomogeneous. A convenient term is the b vector. To be conformable for multiplication by a matrix, the dimension of a row vector must be the same as the column dimension of the matrix. A column vector must have the same dimension as the row dimension of the matrix.

Designating the two vectors and one matrix just defined by boldface letters, the set of equations (2-44) is

Ax ¼ b

ð2-46Þ

Equation (2-46) is a matrix equation because vectors x and b are properly regarded as one-column matrices. Vectors are often differentiated from matrices by writing them as lower case letters.

Multiplication by the rules of matrix algebra produces equation set (2-44) from Eq. (2-46), demonstrating their equivalence. Equation (2-46) is an economical way of expressing Eqs. (2-44), especially where n is large, but it is more than that: Systematic methods of solving Eqs. (2-44) really depend on the properties of the coefficient matrix and on what we can do with it. For example, if the set of Eqs. (2-44) is linearly dependent, A is singular, which means, among other things, that its determinant is zero and it has no inverse A 1. In practical terms, this means that no unique solution set exists for Eqs. (2-44). We already knew that, but less obvious operations on Eqs. (2-44) such as triangularization and diagonalization can be more easily visualized and programmed in terms of operations on the coefficient matrix A than in terms of the entire set.

Exercise 2-13

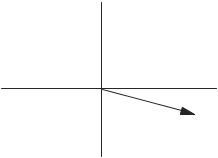
Show that a vector in a plane can be unambiguously represented by an ordered number pair and hence that any ordered number pair can be regarded as a vector.

Solution 2-13

Consider a vector as an arrow in two-dimensional space. Now superimpose x – y coordinates on the 2-space, arbitrarily placing the origin on the ‘‘tail’’of the arrow.

The vector in Fig. 2-2 happens to fall in the fourth quadrant as drawn. The number pair giving the point that coincides with the tip of the arrow gives its magnitude and direction relative to the coordinate system chosen. Magnitude and direction are all that you can know about a vector; hence it is completely defined by the number pair ð5; 1Þ.

In general, a vector in an n-space can be represented by an n-tuple of numbers; for example, a vector in 3-space can be represented as a number triplet.

The determinant having the same form as matrix A,

		a12
det A ¼	a11
	a21	a22

APPLICATIONS OF MATRIX ALGEBRA

47

y

x

(5, –1)

Figure 2-2 A Vector in Two-Dimensional x-y Space.

is not the same as A, because a matrix is an operator and a determinant is a scalar; a matrix is irreducible but a determinant can, if it satisfies some restrictions, be written as a single number.

det A ¼	a11	a12		¼ a11a22 a12a21
	a21	a22

Algorithms

An algorithm is a recipe for solving a computational problem. It gives the general approach but does not go into specific detail. Although there are many algorithms for simultaneous equation solving in the literature, they can be separated into two classes: elimination and iterative substitution. Elimination methods are closed methods; in principle, they are capable of infinite accuracy. Iterative methods converge on the solution set, and so, strictly speaking, they are never more than approximations. In practice, the distinction is not so great as it might seem, because iterative approximations can be made highly self-consistent, that is, nearly identical from one iteration to the next, and closed elimination methods suffer the same machine word-size limitations that prevent infinite accuracy in any fairly involved computer procedure.

Gaussian Elimination. In the most elementary use of Gaussian elimination, the first of a pair of simultaneous equations is multiplied by a constant so as to make one of its coefficients equal to the corresponding coefficient in the second equation. Subtraction eliminates one term in the second equation, permitting solution of the equation pair.

Solving several equations by the method of Gaussian elimination, one might divide the first equation by a11 , obtaining 1 in the a11 position. Multiplying a21 into the first equation makes a11 ¼ a21. Now subtracting the first equation from the second, a zero is produced in the a21 position. The same thing can be done to produce a zero in the a31 position and so on, until the first column of the coefficient matrix is filled with zeros except for the a11 position.

48	COMPUTATIONAL CHEMISTRY USING THE PC

Attacking the a22 position in the same way, but leaving the first horizontal row of the coefficient matrix alone, yields a matrix with zeros in the first two columns except for the triangle

01

a11 a12 a13

B0 a22 23 C

BCa

	0	0	a33			C
B ..		..	..		. .
@	. . . .					A

This is continued n 1 times until the entire coefficient matrix has been converted to an upper triangular matrix, that is, a matrix with only zeros below the principal diagonal. The b vector is operated on with exactly the same sequence of operations as the coefficient matrix. The last equation at the very bottom of the triangle, annxn ¼ bn, is one equation in one unknown. It can be solved for xn, which is backsubstituted into the equation above it to obtain xn 1 and so on, until the entire solution set has been generated.

Exercise 2-14

In Exercise 2-8, we obtained the least equation of the matrix

A ¼	2	1
	1	3

Solve the simultaneous equation set by Gaussian elimination

2x þ y ¼ 4

x þ 3y ¼ 7

Note that the matrix from Exercise 2-8 is the matrix of coefficients in this simultaneous equation set. Note also the similarity in method between finding the least equation and Gaussian elimination.

Solution 2-14

The triangular matrix AG resulting from Gaussian elimination is

G	¼	1 0:5
A		2:5

In the process of obtaining the upper triangular matrix, the nonhomogeneous vector has

been transformed to	52 . The bottom equation of Ax ¼ b
x þ 0:5y ¼ 2	ð	2-47	Þ
2:5y ¼ 5

APPLICATIONS OF MATRIX ALGEBRA

49

yields y ¼ 2. Back-substitution into the top equation yields x ¼ 1. The solution set, as one

could have seen by inspection, is						1	. Mathcad, after the matrix A and the vector b have
						2
been defined by using the full					colon keystroke, solves the problem using the lsolve
command	3	b :¼ 7
A :¼ 1
2	1			4
lsolveðA; bÞ ¼			2
			1

Exercise 2-15

Write a program in BASIC for solving linear nonhomogeneous simultaneous equations by Gaussian elimination and test it by solving the equation set in Exercise 2-13.

In the computer algorithm, division by the diagonal element, multiplication, and subtraction are usually carried out at the same time on each target element in the

coefficient matrix, leading to some term like ajk aik	aji	. Next, the same three
	aii
the b vector. The arithmetic
combined operations are carried out on the elements of

statements are simple, as is the procedure for back-substitution. The trick in writing a successful Gaussian elimination program is in constructing a looping structure and keeping the variable indices straight so that the right operations are being carried out on the right elements in the right sequence.

Gauss–Jordan Elimination. It is possible to continue the elimination process to remove nonzero elements above the principal diagonal, leaving only aii 6¼0 in the coefficient matrix. This extension of the Gaussian elimination method is called the Gauss–Jordan method. By exchanging columns (which does not change the solution set) one can switch the largest element in each row of the coefficient matrix into the pivotal position aii, and most Gauss–Jordan programs do this. Once the coefficient matrix has been completely diagonalized so that the aii are the only nonzero elements, and the same operations have been carried out on the b vector, the original system of n equations in n unknowns has been reduced to n equations, each in one unknown. The solution set follows routinely.

Exercise 2-16

Extend the matrix triangularization procedure in Exercise 2-14 by the Gauss–Jordan

procedure to obtain the fully diagonalized matrix		1	0		and the b vector	1	. The
solution set follows routinely.		0	0:5			1

By Cramer’s rule, each solution of Eqs. (2-44) is given as the ratio of determinants

xi ¼	Di	ð2-48Þ
	D

50	COMPUTATIONAL CHEMISTRY USING THE PC

where D is the determinant of the coefficients aij and Di is a similar determinant in which the ith column has been replaced by the b vector. The method is open-ended, that is, it can be applied to any number of equations containing the same number of unknowns, resulting in n þ 1 determinants of dimension n n.

Exercise 2-17

Solve the equation set of Eqs. (2-44) using Cramer’s rule.

Although apparently quite different from the Gauss and Gauss–Jordan methods, it turns out that the most efficient method of reducing large determinants is mathematically equivalent to Gaussian elimination. As far as the computer programming is concerned, the method of Cramer’s rule is only a variant on the Gaussian elimination method. It is slower because it requires evaluation of several determinants rather than triangularization or diagonalization of one matrix; hence it is not favored, except where the determinants are needed for something else. Determinants have one property that is very important in what will follow. If a row is exchanged with another row or a column is exchanged with another column, the determinant changes sign.

Exercise 2-18

Verify the preceding statement for the determinant

det M ¼		1	2
		3	4

Solution 2-18

3 4				¼ 4 6 ¼ 2	4 3				¼ 6 4 ¼ 2
	1	2				2	1

The Gauss–Seidel Iterative Method. The Gauss-Seidel iterative method uses substitution in a way that is well suited to machine computation and is quite easy to code. One guesses a solution for x1 in Eqs. (2-44)

a11x1 þ a12x2 ¼ b1

ð2-49Þ

a21x1 þ a22x2 ¼ b2

and substitutes this guess into the first equation, which leads to a solution for x2. The solution is wrong, of course, because x1 was only a guess, but, when substituted into the second equation, it gives a solution for x1. That solution is also wrong, but, under some circumstances, it is less wrong than the original guess. The new

APPLICATIONS OF MATRIX ALGEBRA

51

approximation to x1 is substituted to obtain a new x2 and so on in an iterative loop, until self-consistency is obtained within some small predetermined limit.

The drawback of the Gauss–Seidel method is that the iterative series does not always converge. Nonconvergence can be spotted by printing the approximate solution on each iteration. A favorable condition for convergence is dominance of the principal diagonal. Some Gauss–Seidel programs arrange the rows and columns of the coefficient matrix so that this condition is, insofar as possible, satisfied. A more detailed discussion of convergence is given in advanced texts (Rice, 1983; Norris, 1981).

Matrix Inversion and Diagonalization

Looking at the matrix equation Ax ¼ b, one would be tempted to divide both sides by matrix A to obtain the solution set x ¼ b=A. Unfortunately, division by a matrix is not defined, but for some matrices, including nonsingular coefficient matrices, the inverse of A is defined.

The unit matrix, I, with aii ¼ 1 and aij ¼ 0 for i 6¼j, plays the same role in matrix algebra that the number 1 plays in ordinary algebra. In ordinary algebra, we can perform an operation on any number, say 5, to reduce it to 1 (divide by 5). If we do the same operation on 1, we obtain the inverse of 5, namely, 1/5. Analogously, in matrix algebra, if we carry out a series of operations on A to reduce it to the unit matrix and carry out the same series of operations on the unit matrix itself, we obtain the inverse of the original matrix A 1.

One series of mathematical operations that may be carried out on the coefficient matrix to diagonalize it is the Gauss–Jordan procedure. If each row is then divided by aij, the unit matrix is obtained. Generally, A and the unit matrix are subjected to identical row operations such that as A is reduced to I, I is simultaneously converted to A 1. The computer program written to do this is essentially a Gauss–Jordan program as far as coding and machine considerations are concerned (Isenhour and Jurs, 1971). Alternatively, both reduction of A to I and conversion of I to A 1 may be done by the Gauss–Seidel iterative method (Noggle, 1985).

The attractive feature in matrix inversion is seen by premultiplying both sides of

Ax ¼ b by A 1,

A 1Ax ¼ A 1b ¼ Ix ¼ x ¼ A 1b

ð2-50Þ

This means that once A 1 is known, it can be multiplied into several b vectors to generate a solution set x ¼ A 1b for each b vector. It is easier and faster to multiply a matrix into a vector than it is to solve a set of simultaneous equations over and over for the same coefficient matrix but different b vectors.

Exercise 2-19

Invert the matrix in Exercise 2-8 by row operations.

52	COMPUTATIONAL CHEMISTRY USING THE PC

Solution 2-19

Place the original coefficient matrix next to the unit matrix. Divide row 1 by 2 and subtract the result from row 2. This is a linear operation, and it does not change the solution set.

1	3	0	1 )	0	25	21	1 !
2	1	1	0	1	1	1	0
					2	2

This gives you a zero in the 2,1 position of the original matrix, which is one step along the way of diagonalization. Continue with the necessary operations to diagonalize the coefficient matrix and at the same time perform the same operations on the adjacent unit matrix. On completion of this stepwise procedure, you have the unit matrix on the left and some matrix other than the unit matrix on the right.

1 0 z11 z12

01 z21 z22

Show that the matrix on the right, Z, is the inverse of the original matrix A by multiplying it into A to find ZA ¼ I. Now generate the solution set to the equations for which A is the coefficient matrix by multiplying Z (which is A 1) into the nonhomogeneous vector to obtain the solution set {1, 2}.

COMPUTER PROJECT 2-1 j Simultaneous Spectrophotometric Analysis

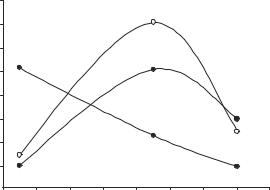
A spectrophotometric problem in simultaneous analysis (Ewing, 1985) is taken from the original research of Weissler (1945), who reacted hydrogen peroxide with Mo, Ti, and V ions in the same solution to produce compounds that absorb light strongly in overlapping peaks with absorbances at 330, 410, and 460 nm, respectively as shown in (Fig. 2-3).

	0.7
	0.6
	0.5
Absorbance	0.4
	0.3
	0.2
	0.1
	0.0
	320	340	360	380	400	420	440	460	480
				Wavelength

Figure 2-3 Visible Absorption Spectra of Peroxide Complexes of Mo, Ti, and V.