Rogers Computational Chemistry Using the PC

CURVE FITTING

63

The slope of the linear function is the minimization parameter. It is the only thing one can change to obtain a ‘‘better’’ fit to points for a line passing through the origin. (It is NEVER permissible to ‘‘adjust’’ experimental points.) The slope calculated by the least squares method is the ‘‘best’’ slope that can be obtained under the assumptions. Once one knows the slope of a linear function passing through the origin, one knows all that can be known about that function.

Exercise 3-2

Using a hand calculator, find the slope of the linear regression line that passes through the origin and best satisfies the points

x 1:0 2:0 3:0 4:0 5:0

y1:1 1:9 2:9 4:0 4:8

Solution 3-2

Scanning the data set, it is evident that the slope should be slightly less than 1.0.

5

X

xiyi ¼ 53:6

1

5

X

x2i ¼ 55:0

1

Pn

m ¼ Pi¼1 xiyi ¼ 0:97

n¼ x2 i 1 i

Linear Functions Not Passing Through the Origin

Deviations from a curve thought to be a straight line y ¼ mx þ b, not passing through the origin (b 6¼0), are

ðmxi þ bÞ yi ¼ di

ð3-9Þ

Note that m and b do not have subscripts because there is only one slope and one intercept; they are the minimization parameters for the least squares function.

Now there are two minimization conditions

q

n

2

q

n

2

X

di

¼

X

ðmxi þ b yiÞ

¼ 0

ð3-10aÞ

qb i ¼1

qb

i ¼1

and

q

n

2

q

n

2

X

¼

X

ðmxi þ b yiÞ

¼ 0

ð3-10bÞ

qm i ¼1

di

qm

i ¼1

64	COMPUTATIONAL CHEMISTRY USING THE PC

which must be satisfied simultaneously. Carrying out the differentiation, one obtains

n	n		n
X	X	b	X	¼ 0	ð3-11aÞ
mxi þ			yi
i ¼1	i ¼1		i ¼1
and
n	n		n
X	X		X	xiyi ¼ 0	ð3-11bÞ
mxi2 þ		bxi
i ¼1	i ¼1		i ¼1
which are called the normal equations. Rewriting them as
n		n
X		X			ð3-12aÞ
nb þ	xim ¼		yi
i ¼1		i ¼1
n	n		n
X	X		X		ð3-12bÞ
xib þ	xi2m ¼			xiyi
i ¼1	i ¼1		i ¼1

makes it clear that the intercept and slope are the two elements in the solution vector of a pair of simultaneous equations

	i 1 xi	Pi 1 xi2 m		¼	Pi 1 xiyi		ð Þ
		n			n
	n	i¼1 xi	b		i¼1 yi		3-13
	P ¼	P ¼			P ¼
	n	n			n

The coefficient matrix and nonhomogeneous vector can be made up simply by taking sums of the experimental results or the sums of squares or products of results, all of which are real numbers readily calculated from the data set.

Solving the normal equations by Cramer’s rule leads to the solution set in determinantal form

b ¼		Db							ð3-14aÞ
		D
and
m ¼			Dm						ð3-14bÞ
			D
or		Pn				Px2	P x	P
	¼								ð		Þ
b				yi		xi2	xiyi	yi		3-15a
							P i
					P i
								2

CURVE FITTING								65
and		P			P P
m	¼	n	xiyi		xi	yi	ð	3-15b	Þ
						2
		n	x2		x
			P i		P i

where the limits on the sums, i ¼ 1 n, have been dropped to simplify the appearance of the equation. Equations (3-15) are in the form usually given in elementary treatments of least squares data fitting in analytical and physical chemistry laboratory texts.

Exercise 3-3

Find the slope and intercept of a straight line not passing through the origin of the data set

x 1:0 2:0 3:0 4:0 5:0

y3:1 3:9 4:9 6:0 6:8

Solution 3-3

Using Mathcad, we regard the data set as two vectors x ¼ f1:0; 2:0; 3:0; 4:0; 5:0g and y ¼ f3:1; 3:9; 4:9; 6:0; 6:8g. They are defined using the : keystroke for a 5 1 matrix

0 1

0

1

13:1

x :	B 3 C			y :		B 4:9 C
	¼ B	2	C		¼ B		3:9	C
	B	4 C				B	6:0 C
	B		C			B		C
	B	5 C				B	6:8 C
	B		C			B		C
	@ A					@		A
		slopeðx; yÞ ¼				0:95
	interceptðx; yÞ ¼					2:09

One might have expected the same slope for this function as for the function described in Exercise 3-2 because the y vector in this exercise is nothing but the y vector in Exercise 3-2 with 2.0 added to each element. Calculating the slope and intercept adds flexibility to the problem. Now the intercept that had been constrained to 0.0 in Exercise 3-2 is free to move a little, giving a better fit to the points. We find a slightly different slope and an intercept that is slightly different from the anticipated 2.0. The slope and intercept for this exercise should be reported as 0.95 and 2.1, retaining two significant figures.

If we go back and calculate the slope and intercept for the data set in Exercise 3-2 without the constraint that the line must pass through the origin, we get the solution vector {0.95, 0.09} for a line parallel to the line in Exercise 3-3 and 2.0 units distant from it, as expected.

Quadratic Functions

Many experimental functions approach linearity but are not really linear. (Many were historically thought to be linear until accurate experimental determinations

66	COMPUTATIONAL CHEMISTRY USING THE PC

showed some degree of nonlinearity.) Nearly linear behavior is often well represented by a quadratic equation

y ¼ a þ bx þ cx2

ð3-16Þ

The least squares derivation for quadratics is the same as it was for linear equations except that one more term is carried through the derivation and, of course, there are three normal equations rather than two. Random deviations from a quadratic are

	a þ bxi þ cxi2 yi ¼ di				ð3-17Þ
The minimization conditions are
	q	n	2	¼ 0	ð3-18aÞ
	qa i¼1		di
		X
	q	n	2	¼ 0	ð3-18bÞ
	qb i¼1		di
		X
	q	n	2	¼ 0	ð3-18cÞ
	qc i¼1		di
		X

which must be true simultaneously. Solution of these equations leads to the normal equations

þ

X

2

þ

X

3

¼ X

ð

Þ

X

na

þ

b

xi

þ

c

xi2

yi

ð

3-19a

Þ

2

X 3

X 4

¼ X 2

a

xi

b

xi

c

xi

xiyi

3-19b

a X xi

þ b X xi

þ c X xi

¼ X xi yi

ð3-19cÞ

with the solution vector {a; b; c} and the nonhomogeneous vector {

yi;

xiyi;

P

P P

xi2yi}. The matrix form of the set of normal equations is

0

a

B P @ xi

P

x2i

or simply

Pxi2	P xi3	10 b 1	¼	0 Pxiyi	1	ð3-20Þ
xi	xi2	a		yi	C
P xi3	P xi4	CB c C		B Pxi2yi
P	P	A@ A		@ P	A

Qs ¼ t

ð3-21Þ

where the meaning of matrix Q and vectors s and t are evident from Eq. (3-20). A general-purpose linear least squares program QLLSQ and a quadratic least squares program QQLSQ can be downloaded from www.wiley.com/go/computational. Others are available elsewhere (Carley and Morgan, 1989). The input format given in QQLSQ is used to solve Exercise 3-4.

CURVE FITTING

67

Exercise 3-4

From the theory of the electrochemical cell, the potential in volts E of a silver-silver chloride-hydrogen cell is related to the molarity m of HCl by the equation

	2RT		2:342 RT
E þ		ln m ¼ E þ		m1=2	ð3-22Þ
	F		F

where R is the gas constant, F is the Faraday constant ð9:648 104 coulombs mol 1Þ, and T is 298.15 K. The silver-silver chloride half-cell potential E is of critical importance in the theory of electrochemical cells and in the measurement of pH. (For a full treatment of this problem, see Mc Quarrie and Simon, 1999.) We can measure E at known values of m, and it would seem that simply solving Eq. (3-22) would lead to E . So it would, except for the influence of nonideality on E. Interionic interference gives us an incorrect value of E at any nonzero value of m. But if m is zero, there are no ions to give a voltage E. What do we do now?

The way out of this dilemma is to make measurements at several (nonideal) molarities m and extrapolate the results to a hypothetical value of E at m ¼ 0. In so doing we have ‘‘extrapolated out’’ the nonideality because at m ¼ 0 all solutions are ideal. Rather than ponder the philosophical meaning of a solution in which the solute is not there, it is better to concentrate on the error due to interionic interactions, which becomes smaller and smaller as the ions become more widely separated. At the extrapolated value of m ¼ 0, ions have been moved to an infinite distance where they cannot interact.

Plotting the left side of Eq. (3-22) as a function of m1=2 gives a curve with 2:342 RT
		F
as the slope and E as the intercept. Ionic interference causes this function to deviate
from linearity at m 6¼0, but the limiting (ideal) slope and intercept are		approached
			1=2
the left side of Eq. (3-22) as a function of m
as m ! 0. Table 3-1 gives values of 1=2				.
The concentration axis is given as m	in the corresponding Fig. 3-1 because there

are two ions present for each mole of a 1-1 electrolyte and the concentration variable for one ion is simply the square root of the concentration of both ions taken together.

The problem now is to find the best value of the intercept on the vertical axis. We can do this by fitting the experimental points to a parabola.

Solution 3-4

TableCurve gives {.2225, .05621, .06226} for a, b, and c of the quadratic fit, and program QQLSQ gives f0:2225; 5:621 10 2, and 6:226 10 2 (note that the order of terms is reversed in Output 3-4).

Table 3-1 The Left Side of Eq. 3-4 at Seven Values of m1=2

m1=2	E þ 2RTF ln m
.05670	.2256
.07496	.2263
.09559	.2273
.1158	.2282
.1601	.2300
.2322	.2322
.3519	.2346

68	COMPUTATIONAL CHEMISTRY USING THE PC

m/F)ln

T+(2R E

0.236

0.232

0.228

0.224

0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40
				m1/2

Figure 3-1 Voltage Measurements on a Silver-Silver Chloride, Hydrogen Cell at 298.15 K. The contribution of the Standard Hydrogen Electrode is taken as zero by convention.

Output 3-4

Program QQLSQ

How many data pairs? 7

THE FOLLOWING DATA PAIRS WERE USED:

X	Y	YEXPECTED
.0567	.2256	.2255161
.07496	.2263	.2263927
.09559	.2273	.2273332
.1158	.2282	.2282032
.1601	.23	.2299322
.2322	.2322	.2322238
.3519	.2346	.2345989

THE EQUATION OF THE PARABOLA IS:

Y ¼ 6:225745E-02X 2 þ ð5:620676E-02ÞX þ ð:2225293Þ

THE STANDARD DEVIATION OF Y VALUES IS 6.04448E-05

The two estimates for the first or a parameter of the parabolic fit are the intercepts on the voltage axis of Fig. 3-1, so both procedures arrive at a standard potential of the silversilver chloride half-cell of 0.2225 V. The accepted modern value is 0.2223 V (Barrow, 1996).

Polynomials of Higher Degree

The form of the symmetric matrix of coefficients in Eq. 3-20 for the normal equations of the quadratic is very regular, suggesting a simple expansion to higherdegree equations. The coefficient matrix for a cubic fitting equation is a 4 4

CURVE FITTING

69

matrix with x6i in the 4, 4 position, the fourth-degree equation has x8i in the 5, 5 position, and so on. It is routine (and tedious) to extend the method to higher degrees. Frequently, the experimental data are not sufficiently accurate to support higher-degree calculations and ‘‘differences’’ in fitting equations higher than the fourth degree are artifacts of the calculation rather than features of the data set.

Statistical Criteria for Curve Fitting

Frequently in curve fitting problems, one has two curves that fit the data set more or less well but they are so similar that it is difficult to decide which is the better curve fit. Commercially available curve fitting programs (e.g., TableCurve, www.spss.com) usually give many curves that fit the data (more or less well). The best of these are often very close in their goodness of fit. One needs an objective statistical criterion of this vague concept, ‘‘goodness of fit.’’

The essential criterion of goodness of fit is nothing more than the sum of squares of deviations as in Eq. (3-4), although this simple fact may be obscured by differences in notation and nomenclature. Starting with the simple case of comparing the fit of straight lines to the same data set, the deviation in minimization criterion (3-4) is referred to as the residual, ð^yi yiÞ, which is the difference between the ith experimental measurement yi and the value ^yi that yi would have if the fit were perfect. The definition ðyi ^yiÞ is also used (Jurs, 1996) because the difference in sign is of no importance when we square the residual. Following Jurs’s nomenclature and notation (Jurs, 1996), the sum of squares of residuals is thought of as the sum of squares due to error, hence the notation SSE

n	n
X	X	ð3-23aÞ
SSE ¼ ð^yi yiÞ2 ¼	ðyi ^yiÞ2
i ¼1	i ¼1

The differences between corresponding elements in ordered sets (vectors) in, for example, columns 2 and 3 of output 3-4 give an ordered set of residuals. In this example, the residual for the first data point is 0:2256 0:2255161 ¼ 8:39 10 5.

SSE is sometimes written

n
X	ð3-23bÞ
SSE ¼ wið^yi yiÞ2

i ¼1

where wi is a weighting factor used to give data points a greater or lesser weight according to some system of estimated reliability. For example, if each data point were the arithmetic mean of experimental results, we might make wi ¼ s20=s2i where s2o is the maximum variance in the set ðw0 ¼ 1Þ and all the other weighting factors are greater than 1 (Wentworth, 2000). For simplicity, let us take wi ¼ 1 for all data in what follows.

70	COMPUTATIONAL CHEMISTRY USING THE PC

The sum of squares of differences between points on the regression line ^yi at xi and the arithmetic mean y is called SSR

	n
SSR ¼	X	ð3-24Þ
	ð^yi yÞ2
	i¼1
The total sum of squared deviations from the mean is
	n
SST ¼	X	ð3-25Þ
	ðyi yÞ2

i¼1

which is made up of two parts, one contribution due to the regression line and one due to the residual or error

SST ¼ SSR þ SSE			ð3-26Þ
Jurs defines a regression coefficient R as
SSR
R2 ¼			ð3-27Þ
	SST

If the fit is very good, the residuals will be small, SST!SSR as SSE!0, hence R2 ! 1:0. If SSE is a substantial part of SST (as it is for a poor curve fit) SSR < SST and R2 < 1:0. In the limit as SSE becomes very large, R2 ! 0.

To reconcile this notation with the output from TableCurve, note that

R2

SSR

SST SSE

1

SSE

3-28

¼ SST

¼

SST

¼

SST

ð

Þ

Now, making only the change in notation of SSM for SST to indicate the total deviation from the mean and changing from upper to lower case r, we have

r2	SSE	ð3-29Þ
	¼ 1 SSM

which is the coefficient of determination as defined in TableCurve (TableCurve User’s Manual, 1992). For an example of r2 calculated by TableCurve, see Exercise 3-5.

Reliability of Fitted Parameters

For a specified mean and standard deviation the number of degrees of freedom for a one-dimensional distribution (see sections on the least squares method and least squares minimization) of n data is ðn 1Þ. This is because, given m and s, for n > 1 (say a half-dozen or more points), the first datum can have any value, the second datum can have any value, and so on, up to n 1. When we come to find the

CURVE FITTING

71

last data point, we have no freedom. There is only one value that will make m and s come out right. If we select anything else, we violate the hypothesis of known m and s.

The situation is similar for a linear curve fit, except that now the data set is twodimensional and the number of degrees of freedom is reduced to ðn 2Þ. The

analogs of the one-dimensional variance s2 ¼ ðPni¼1 di2Þ=ðn 1Þ and the standard deviation s are the mean square error

MSE ¼			SSE		ð3-30Þ
			n 2
and the standard deviation of the regression
s ¼	p				ð3-31Þ
		MSE

for the two-dimensional case.

If the data set is truly normal and the error in y is random about known values of x, residuals will be distributed about the regression line according to a normal or Gaussian distribution. If the distribution is anything else, one of the initial hypotheses has failed. Either the error distribution is not random about the straight line or y ¼ f ðxÞ is not linear.

If the matrix form of the fitting procedure is used to solve for the intercept and

slope of a straight line, Eq. (3-13)

Pi 1 xiyi

ð

Þ

i 1 xi

Pi 1 xi2 m ¼

n

n

n

i¼1 xi

b

i¼1 yi

3-32

P ¼

P ¼

P ¼

n

n

n

yields

¼

Pi 1 xi2

Pi 1 xiyi

ð

Þ

m

i 1 xi

b

n

n

xi

1

n

yi

3-33

P ¼

i¼1

i¼1

P ¼

P ¼

n

n

n

The variance of the regression times the diagonal elements of the inverse coefficient matrix gives the variance of the intercept and slope,

sb2	¼ d11s2	ð3-34aÞ
and
sm2	¼ d22s2	ð3-34bÞ

which lead directly to the standard deviations of the intercept and slope, sb and sm. Their standard deviations are given in TableCurve under the heading Std Error in column 3, block 2 of the Numeric Summary output. We now have

y ¼ a Std Errora þ bx Std Errorb

ð3-35Þ

72	COMPUTATIONAL CHEMISTRY USING THE PC

as the equation of our straight line fit. Further treatment, which we shall not go into here, involves finding the t value for each parameter and establishing the confidence limits at some confidence level, for example, 90%, 95%, or 99% (Rogers, 1983). These limits are given in block 2 of the TableCurve output. The confidence level can be specified in TableCurve by clicking the intervals button in the Review Curve-Fit window. The default value is 95%.

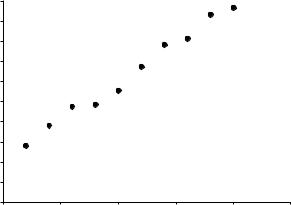
Exercise 3-5

Fit a linear equation to the following data set and give the uncertainties of the slope and intercept (Fig. 3-2).

x	0:400	0:800 1:20	1:60	2:00	2:40	2:80	3:20	3:60	4:00
y	2:79	3:82 4:75	4:85	5:55	6:71	7:81	8:12	9:31	9:65

Solution 3-5

Working the problem by the matrix method we get

m

¼

22

61:6

164:804

b

10

22

1

63:36

¼

0:167

0:076

164:804

¼

1:92

0:467

0:167

63:36

2:10

Solved using the BASIC curve fitting program QLLSQ we get as a partial output block

10 POINTS, FIT WITH STD DEV OF THE REGRESSION .2842293

Y Data

10

9

8

7

6

5

4

3

2

1

0

0

1

2

3

4

5

X Data

Figure 3-2 Data Set for Exercise 3-5.