II. МЕТОДИКА АНАЛИЗА ВРЕМЕННЫХ РЯДОВ

2.1. Вычисление полиномиального тренда

При анализе временных рядов вариаций потока космических лучей f(t) будем исходить из общго предположения, что их можно представить в виде суммы нескольких аддитивных компонент:

f(t) = ftr(t) + fp(t) + far(t) + ε(t),

где: ftr(t) – медленная нерегулярная составляющая, называемая трендом;

fp(t) – периодическая компонента (не обязательно гармоническая) или сумма нескольких подобных компонент;

far(t) – быстрые нерегулярные малые вариации, которые включают в себя все, что не укладывается в принятую модель для периодических компонент;

ε(t) – случайная составляющая, которая описывается случайным процессом определенного типа (например, пуассоновским).

Из математики известно, что функции вида f(t) = ftr(t) + ε(t) хорошо описываются в рамках теории аппроксимации (при малом вкладе ε(t)) или методом наименьших квадратов (при больших ε(t)); для f(t) = fp(t) хорошо работает теория гармонических рядов Фурье. Однако для функции вида f(t) = fp(t) + ε(t) при больших значениях ε(t) теория фурье-анализа становится мало эффективной для выявления полезных сигналов. Для функций вида f(t) = ftr(t) + fp(t) при отсутствии априорной информации о характере тренда выявление полезных сигналов также становится затруднительным. В этом случае могут возникать искусственные высокочастотные периодичности в ряду остатков или, наоборот, уничтожаться существующие компоненты.

Ряды счета мюонов КЛ не являются стационарными. Даже при спокойной гелиообстановке, когда поток КЛ практически постоянен и изотропен, могут возникать вариации вторичных атмосферных мюонов за счет метеоэффектов. В экспериментах с нейтронными мониторами метеоэффекты учитываются достаточно просто за счет коррекции интенсивности на изменение полного столба атмосферного давления, которое синхронно измеряется в месте расположения установки. Температурный эффект для ядер-

42

ноактивной компоненты мал. Поэтому не требуется вносить температурные поправки в данные нейтронных мониторов.

Аналогично проводится коррекция потока мюонов на барометрический эффект. Для исправления данных по мюонам на температурный эффект, надо знать распределение температуры атмосферы по высоте. Измерение приземной температуры, по аналогии с давлением, не отражает температуру столба атмосферы даже в среднем. Это вносит методические неопределенности в анализ вариаций временных рядов потока мюонов.

Колебания давления и температуры приводят к медленным изменениям интенсивности мюонов на протяжении суточных отрезков времени. В дальнейшем на суточных временных рядах будет проводиться частотный анализ, который требует стационарности (среднее значение и дисперсия должны оставаться постоянными на любом участке ряда). Для корректной подготовки временных рядов к фурье- и вейвлет-анализу предварительно вычисляется медленный тренд чисто математическими методами, без учета метеоэффектов.

Имеется много различных способов вычисления тренда, однако не существует универсального рецепта, пригодного для анализа временных рядов различных физических процессов. В данном случае изучаются сравнительно высокочастотные вариации в поведении интенсивности мюонов, с периодами от двух минут до нескольких часов. Минимальный период (2 мин) ограничен дискретностью шага измерений по времени (1 мин). Максимальный период обусловлен решением физических задач, связанных с высокочастотными вариациями КЛ.

С математической точки зрения функция счета мюонов yi измеряется равномерно по времени ti (с постоянным шагом ti = i×τ, где τ – интервал времени) и имеет практически одинаковые веса

(~ 1/σi2 ) в пределах каждого ряда матрицы, обусловленные стати-

стической точностью. При этом вариация счета мюонов составляет несколько процентов и поэтому мало влияет на изменение веса в отдельных точках временного ряда. Для рядов такого типа наиболее оптимально вычислять тренд fl (t) с помощью ортогональных полиномов Чебышева с показателем степени не выше l:

43

	fl (t ) = K0ψ0 + K1ψ1 (t )+...Klψl (t),
где	K0 = ∑yi n; ...	Kl = ∑yiψl (ti ) ∑ψl2 (ti ).

Суммирование проводится по всем точкам ряда i: от 1 до n. Значения показателя степени полинома l могут быть от 0 до (n–1). Первые два полинома записываются в виде:

ψ0 (t )=1;	ψ1	(ti )= ti −	n +1	.
		2

Ортогональные полиномы более высоких степеней получаются по рекуррентной формуле:

ψl +1 (t) =ψ1 (t )×ψl (t )− l2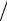(n2 −l2 )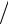(4(4l2 −1)) ×ψl −1 (t).

Полиномы Чебышева обеспечивают достаточно равномерное приближение к экспериментальным точкам yi на всем отрезке времени экспозиции.

Вычисление тренда проводится последовательным увеличением степени полиномов l, при этом подсчитывается среднеквадратичная дисперсия на всем интервале (1 ≤ i ≤ n):

Ml = ∑ fl (ti )− yi 2 .

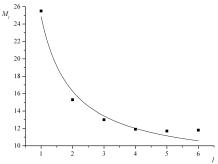
На рис. 2.1 приведен пример поведения Ml для ряда длительностью 5 часов. Видно, что при l 3÷4 происходит резкий спад величины Ml, после которого среднеквадратичная дисперсия плавно убывает.

Наилучший порядок значения l определяется с помощью критерия Фишера. Для этого на каждом шаге по l находится оценка дисперсии аппроксимации, приведенная к одной степени свободы:

Sl2 = Ml 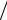(n −(l +1)). Значение Sl2 сопоставляется с величиной Sl2−1 оценки дисперсии на предыдущем шаге по l.

Если Sl2−1 > Sl2 , при условии (Sl2−1 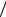Sl2 )> F1−α (n −l,n −l −1), то разница дисперсий значима и порядок полинома l надо увеличить.

44

В противном случае, нужно остановиться на полиноме (l − 1) порядка. Переменная F1−α есть функция Фишера. Такое сравнение значимостей справедливо для нормального распределения погрешностей. Дальнейшее повышение степени полинома приведет к уменьшению чувствительности метода для выделения случайной компоненты. Полином с максимально возможным показателем степени пройдет практически через все экспериментальные точки, и случайная компонента не будет идентифицирована.

Рис. 2.1. Результат аппроксимации временного ряда мюонов Nμ(t) полиномами Чебышева различной степени l. Величина Мl − сумма квадратов отклонений (условн. ед.) между полиномом и экспериментальными данными временного ряда

Практически для большинства случаев значение l можно брать равным 3–4, а длина рядов изменяется по i в пределах 180−300 точек, что соответствует времени экспозиции 3–5 часов.

На рис. 2.2 приведен пример обработки трехчасового временного ряда: вычисление тренда, выделение остатков ряда (центри-

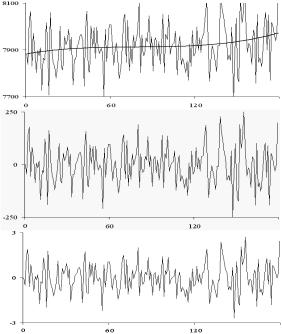
рование) yi = yi − fl (ti ) и их нормализация yi 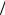σ . Величина σ − среднеквадратичное отклонение в ряду. Остатки ряда yi хорошо

согласуются с гауссовым распределением. Данные рисунки относятся к счету мюонов в относительно спокойных условиях в гелиосфере и атмосфере Земли.

Интенсивность мюонов во временной последовательности отдельных ячеек матричных данных Nik(t) представляет собой сово-

45

купность независимых временных рядов, которые преобразуются в нормированные ряды nik (t) :

nik (t) = (Nik (t) − fl (t)) / σik .

Матрицы nik(t) получаются свободными от угловой зависимости потока атмосферных мюонов (~ cos 2 θ) и влияния светосилы установки, которая изменяется при разных углах регистрации частиц.

Рис. 2.2. Пример выравнивания трехчасового временного ряда матричных данных Nik(t). Верхний график – исходный ряд и полином Чебышева третьей степени; средний – центрированный временной ряд (остатки); нижний – нормированный временной ряд

На рис. 2.3 приведены примеры исходной Nik(t) и нормированной nik(t) матриц для определенного момента времени.

46