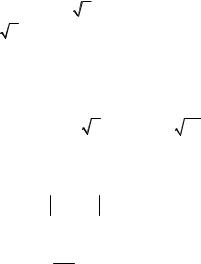
Из вида вейвлета Морле следует, что с его помощью хорошо выявлять квазипериодические вариации с модуляцией частоты. Прямое вейвлет-преобразование записывается в виде

	W (a,b)=	1	∫ y(t)Ψ t −b	dt .
		a
			a

Коэффициент 1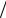 a сохраняет норму вейвлета при изменении мас-

штаба а.

Для практических расчетов удобно проводить дискретизацию параметров a и b. Это обычно проводится через степени числа два:

a = 2

m

; b = k 2

m

; ψmk =

1

t −b

1

Ψ(2

−m

t − k ),

Ψ

=

a

a

2m

где m и k целые числа. В этом случае плоскость аргументов (ab) превращается в сетку ячеек (mk). Отдельный вейвлет охватывает определенный частотный диапазон.

Величина S (a,b)= W (a,b)2 – скалограмма (scalogram) явля-

ется аналогом мощности вариаций для момента времени t b.

Выражение G (a)= 1T ∫S (a,b)db характеризует спектр ва-

риаций и по сути представляет собой аналог сглаженной периодограммы Фурье-преобразования (плотность спектра мощности).

Для получения полной мощности Р следует провести суммирование по всем значениям а:

P = ∫G (a)da .

Величина Р характеризует полную мощность вариаций, просуммированную по всем частотам и сдвигам по времени, в пределах интервала времени усреднения. Для изучения поведения функции Р на продолжительном отрезке времени необходимо последовательно вычислять значения Р на отдельных интервалах.

2.4. Сингулярно-спектральный анализ

Выше упоминалось, что исследуемые физические временные ряды y(t), как правило, являются нестационарными и имеют тренд,

52

вид которого изменяется во времени и априорио не известен. Существующий математический аппарат сингулярно-спектрального анализа (SSA) позволяет вычислить и удалить этот тренд из имеющегося набора данных y(ti) без применения модельных представлений о характере тренда. С помощью метода SSA можно также отделять случайную компоненту (на определенном уровне значимости) от периодической, для дальнейшего более точного анализа характеристик оставшихся одной или нескольких периодических компонент.

Рассмотрим кратко методику анализа одномерного временного ряда y(ti), образованного последовательностью N равноотстоящих значений функции:

yi = fi = f (iτ ), где i = 1, 2, … N, τ − шаг по времени. Выбираем число M < N, которое определяет длину временного

окна. Введем число k = N−(M−1), равное числу векторов разложения при преобразовании временного ряда yi в двухмерную матрицу:

	y1			y2		y3	… yk
	y2			y3		y4	… yk +1
Y =	y3			y4		y5	… yk +2
	…		…		…		…	…
	y	M	y	M +1	y	M +2	…	y	N

Выбор параметра m зависит от характера решаемой задачи. Далее строится матрица S = YY T, которая получается неотри-

цательной и симметричной, где Y T – транспонированная матрица. Собственные значения (λ) матрицы S неотрицательны:

λ1, λ2, … λM > 0. Максимальное число d (из набора i = 1, …, M) для которого λi ≠ 0 определяет порядок сингулярного разложения. Матрица S имеет набор ортонормированных собственных векто-

ров: U	,U		,...U	M	. Можно ввести матрицы вида V =	1	Y T U	,
		2
1					i		i
						λi

где i = 1, …, M. Эти тройки образуют i-компоненты сингулярного разложения матрицы Y:

53

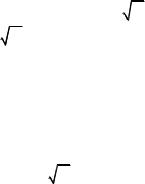
Y = Y + Y + … +Y , где		Y =	λ U V T .
1 2	i	i	i i i

Сингулярные числа σi = λi отражают величину вклада отдель-

ных элементарных матриц. Выбирая разные значения (например, imax = k, где k < M) в сумме Yi с учетом убывания вклада значений σi можно отсечь случайный шум.

Таким образом, для восстановления матрицы Y может быть использована модель меньшей размерности (например, без учета вклада λM):

M −1

Yij = ∑Uik λi Vkj +εij , k =1

где εij − остаток, характеризующий случайную компоненту.

По полученной матрице Yij можно восстановить временной

ряд yi , используя математический аппарат SSA (например, про-

граммный пакет «Гусеница») и учесть вклад тренда (исключить), а затем провести анализ отдельных гармонических компонент. В этом алгоритме используется тот факт, что при наличии в рядуостатке yi гармонических компонент, соседние собственные зна-

чения λi и λi +1 оказываются близкими по величине (в идеале должны совпадать). При этом трендовая составляющая оказывается непарной, и как правило, отвечает самому большему значению λi.

Ниже приведен пример анализа гармонических компонент временного ряда, состоящего из трех синусоид, две из которых имеют целый период (T1, T2), а третья (T3) − дробный:

			2π			2π			2π		+ xn ,
	fn = k1	sin		n	+ k2 sin		n	+ k3 sin		n
			T1			T2			T3

где k1 = 3, T1 = 8, k2 = 2,5, T2 = 5, k3 = 2, T3 = 5/12;

xn – белый шум. Значения n, точки временного ряда, меняются в пределах 1 ≤ n ≤ 120. Длина ряда небольшая – 120 точек. Обработка проводилась для окна М = 30. В системе SSA имеется визуальная возможность следить за поведением парных соседних значений λi и λi +1. В случае их принадлежности к одному и тому же гармоническому колебанию с постоянной амплитудой на двух-

54

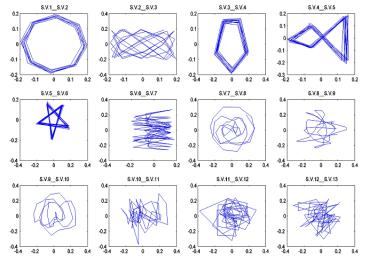
мерном графике (синус-косинус) должна наблюдаться картина, близкая к правильному T-многоугольнику (типа известных из курса физики фигур Лиссажу). Из рис. 2.5 видно, что для парных значений (λ1 и λ2), (λ3, λ4) получаются правильные восьми- и пятиугольники, что соответствует Т1 = 8 и Т2 = 5. Для (λ5 , λ6) фигура получается в виде пятиконечной звезды. Фигура в виде звезды получается для дробного периода сигнала. На окружности фиксируются точки, которые соответствуют углам 4π / 5 , 8π / 5 , 2π / 5 , 6π / 5 , 0. Далее углы повторяются. Таким образом, графики позволяют наглядно, в интерактивном режиме выделять периодические компоненты временного ряда.

При анализе скрытых периодичностей целесообразно проводить комплексный анализ с последовательным применением SSA, вейвлетили фурье-преобразований. Сначала с помощью SSA можно предварительно «вычистить» временной ряд от тренда и шумовых компонент.

Рис. 2.5. Поведение в зависимости от времени (параметрическое) соседних собственных значений λi и λi+1 (слева

направо и сверху вниз): начало−λ1 и λ2 ; конец−λ12 и λ13 . Пятиконечная звезда соответствует значениям λ5 и λ6

55