Данные nik(t) отражают пуассоновский характер потока КЛ для спокойных условий. Видно, что в условиях спокойного состояния гелиосферы, магнитосферы и атмосферы Земли на нормированных снимках-матрицах nik(t) отсутствуют какие-либо непрерывные области с выделенными значениями превышения (или недостатка) в потоке космических лучей. На снимке «пуассоновская рябь»

Рис. 2.3. Слева – матричные данные Nik интенсивности мюонов (64×64 ячейки центральной части матрицы) установки ТЕМП. Контуры соседних полос соответствуют изменению потока мюонов на 10% от его максимальной величины; справа – та же матрица пространственной интенсивности мюонов в относительных отклонениях nik для спокойных условий в гелиосфере и атмосфере Земли. Темный цвет: данные nik < 0; светлый – nik > 0

(флуктуации относительно среднего уровня в большую и меньшую сторону) распределяется равномерно по всей площади снимка. Это соответствует фоновому состоянию в мюонной диагностике – отсутствию высокоэнергичных динамических возмущений в окружающей среде.

2.2. Оконное преобразование Фурье

Короткопериодные вариации интенсивности КЛ могут нести информацию о динамических процессах из тех областей гелиосферы, магнитосферы и атмосферы Земли, которую они пересекают при своем распространении до попадания в детектор. Как правило,

47

амплитуда таких вариаций мала и не превышает статистических ошибок измерения интенсивности в отдельных точках временного ряда. Поэтому требуется применять специальные методы для выявления «скрытых периодичностей». После приведения временных рядов к стационарному виду возможно применение широко распространенного фурье-анализа.

Известно, что классический метод периодограмм не применим при изучении непродолжительных процессов, поскольку они происходят за конечный отрезок времени и их частотные характеристики могут изменяться за время наблюдения. В этом случае, даже с увеличением длины временного ряда, дисперсия частотной фурье-характеристики не будет уменьшаться. Разработан ряд методов с целью снижения дисперсии периодограммы за счет усреднения обычных и модифицированных периодограмм. Наиболее приемлемо использование метода Блэкмана-Тьюки, который дает практически наименьшую дисперсию при высоком частотном разрешении. В этом методе периодограмма S(f) или функция спектральной плотности (также используется название плотность спектра мощности – ПСМ) получается в результате применения преобразования Фурье к корреляционной функции Rx(t), путем введения запаздывающего окна W(k), где 0 ≤ k ≤ M, где M – ширина временного окна.

Достоинством фурье-анализа со сглаживающим окном является несмещенность оценки спектральной плотности, которая стремится к математическому ожиданию при увеличении длины ряда N, а ее дисперсия D уменьшается до нуля при большом N:

D = b ×S 2 ×M 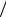N ,

где параметр b ≤ 1 и зависит от типа окна W(k).

Для стационарного нормированного временного ряда y(i) (в диапазоне 1 ≤ i ≤ N) вычисление спектральной плотности S(f) по методу Блэкмана-Тьюки сводится к ряду последовательных процедур. Сначала подсчитывается автоковариационная функция

Ry (k):

Ry (k )= N∑1−k y (i)× y (i + k ) × (N 1− k ),

48

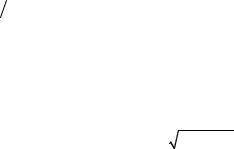
где 0 ≤ k ≤ M. Суммирование проводится в пределах временного окна. Затем выполняется сглаживание функции Ry(k):

Sy (k ) = Ry (k )×W (k )

во всем интервале окна (0 ≤ k ≤ M), где W(k) – одно из распространенных окон типа: Хэмминга, Хеннинга, Парзена и др. В конце вычисляется плотность спектра мощности для разных частот f фурье-преобразования:

	M −1
S( f ) =τ Sy (0)	+ 2∑Sy (k )×cos(2π fkτ )+ Sy (M )×cos(2π fMτ ) ,
	1

где τ − интервал времени между соседними точками временного ряда y(i). Частоты f лежат в диапазоне 0 ≤ f ≤ 0,5τ. Если принять τ = 1, то максимальная частота f max = 0,5 − частота Найквиста, со-

ответствующая минимальному измеримому периоду T min = 2τ (в

данном случае – T min = 2 минуты). Метод Блэкмана-Тьюки, с учетом процедуры сглаживания по частотам, обладает высоким частотным разрешением f ≈1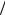τM , которое слабо зависит от вида

сглаживающего окна W.

Для гауссовских временных рядов y(i) статистическое распределение функции спектральной плотности S(f) хорошо согласуется

с χ2 -распределением с числом степеней	свободы	равным
2× N (M ×α), где α − коэффициент порядка	единицы,	значение

которого связано с видом сглаживающего окна W. Для окна Хэмминга значение α 0,8. Теоретическое значение спектральной плотности S(f) для нормированного гауссовского временного ряда является постоянной величиной, равной 1/ (2π) = 0,16 на всех час-

тотах (белый шум), со стандартным среднеквадратическим отклонением σs , равным:

σs = S × α ×M 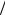N .

Вотсутствие возмущений, временные ряды интенсивности мюонов хорошо согласуются с гауссовским характером флуктуаций, а распределение амплитуд спектральной плотности S(f) под-

чиняется χ2 -распределению. Появление гармонического колеба-

49

ния во временном ряду y(i) будет приводить к увеличению амплитуды функции спектральной плотности S(f0) на отдельной частоте f0 – мощности волны. Ее достоверность достаточно легко оценить как отклонение в χ2 -распределении.

Фурье-анализ при хорошем частотном разрешении, в отличие от вейвлет-преобразования, не обладает временной локализацией волнового процесса. При получении функции спектральной плотности S(f) проводится усреднение по всему отрезку времени заданной экспозиции. Частично этот недостаток можно преодолеть применением дополнительного временного окна, составляющего часть полного рассматриваемого времени экспозиции. Например, можно брать небольшое временное окно продолжительностью 3–5 часов (временной ряд 180–300 одноминутных точек y(i)) при полной суточной экспозиции. В этом окне времени выполняется фу- рье-анализ, затем проводится временной сдвиг (например на 10–15 минут) и снова вычисляется спектральная плотность. Эта процедура рекурентно повторяется вдоль всего суточного ряда. Такой метод расчетов, в виде спектрально-временного анализа (СВАН), получил широкое распространение в различных областях физики, включая исследования динамических процессов вКЛ.

2.3. Вейвлет-анализ

Рассмотренный выше метод фурье-анализа применим для стационарных временных рядов, в которых величина среднего значения функции y(t) и дисперсия (или среднеквадратическое отклонение σ) остаются постоянными на всей длине исследуемого интервала времени. Как правило, большинство гео- и гелиосферических процессов претерпевают эволюцию во времени, что приводит к изменению амплитуды вариаций и частоты соответствующих временных рядов. В этом случае для анализа процесса лучше применять методику вейвлет-преобразований, развитую в последние годы.

Фактически, вейвлет-преобразование аналогично фурьеанализу при разложении исследуемой функции по базовым негар-

моническим функциям солитоноподобного типа: Ψ	t −b
		a	.
	ab

50

Функция Ψab представляет собой короткий волновой пакет, пол-

ная площадь которого (интеграл по времени при фиксированных значениях a, b) равен нулю. Вейвлет (wavelet – короткая волна, или всплеск) Ψab локализован во времени и максимален в облас-

ти времени t ≈ b. Изменение параметра b позволяет «перемещать» функцию-анализатор Ψab по оси времени. Параметр a характери-

зует масштаб вейвлета. Начальный материнский вейвлет устроен так, что при уменьшении масштаба всплеск сжимается и локализуется в пространстве с преобладанием высокочастотной составляющей. При увеличении a – всплеск расширяется и его частота уменьшается. Для любого момента времени изменение а позволяет найти наилучшую корреляцию вейвлета с небольшим куском временного ряда y(t).

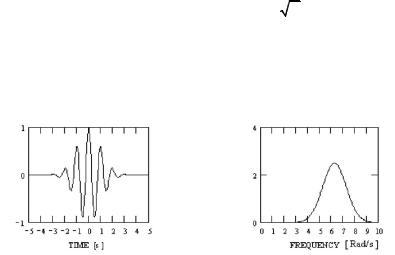
В последние годы разработано много типов материнских вейвлетов, образующих ортонормированные системы различной формы. В качестве примера можно привести материнский вейвлет Морле, имеющий форму синусоподобного цуга, спадающего на концах:

Ψ(t)= eiωot e−t2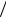α2 ; Ψ(ω)=α πe−α2(π−ω)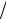4 ,

где ωo – характерная частота, α – параметр затухания. Функция Ψ(t) описывает вейвлет во временной области, Ψ(ω)– в частот-

ной области. На рис. 2.4 приведен пример синусоподобного вейвлета Морле и его частотная характеристика.

Рис. 2.4. Материнский вейвлет Морле во временной области (слева) и его частотная характеристика (справа)

51