Корсун Гидродинамика ЯЕУ Сборник задач и упражнений 2008

Подставляя (2.23.1) в уравнение (2.31), описывающее установившееся распределение скоростей при ламинарном течении жидкости в прямом канале произвольного поперечного сечения, находим, что оно удовлетворяется при значении коэффициента B, равном

	B =	p		a2b2		.	(2.23.2)
		2μ l a2			+ b2

Таким образом, (2.23.1) при коэффициенте B, равном (2.23.2), описывает искомое распределение скорости в эллиптическом канале, так как удовлетворяет и уравнению и граничным условиям.

Средняя скорость в канале определяется интегралом

		b	1−	x2
				a 2
	4	a
u0 =		∫dx	∫
	πab
0			0

Вычисления дают

x2

y2

8B

1

2

3

B(1 −

−

) dy ≡

∫(1 − X

)

2 dX . (2.23.3)

a

2

b

2

3π

0

u0

=

B

≡

p a2b2

.

(2.23.4)

2

4μ l a2

+ b2

Из сравнения (2.23.1) и (2.23.4), следует в частности, что при движении в эллиптической трубе максимальная скорость вдвое превышает среднюю umax = 2u0 при любом соотношении между

длинами полуосей эллипса ab = n .

Соотношение (2.23.4) определяет связь перепада давления в канале p со средней скоростью u0 . Его можно переписать в виде

формулы Дарси (2.32) и определить коэффициент гидравлического сопротивления эллиптической трубы.

	λтр =	A(n)	,	A(n) = 64	2(a2 + b2 )	≡ 64	2(1 + n2 )	.	(2.23.5)
		Re			(a + b)2		(1 + n)2

При определении (2.23.5) учтено, что гидравлический диаметр

	эллиптической трубы равен			dг =	4ab	, а число Рейнольдса
					a +b
		u0dг
	Re =		.
		ν
				91

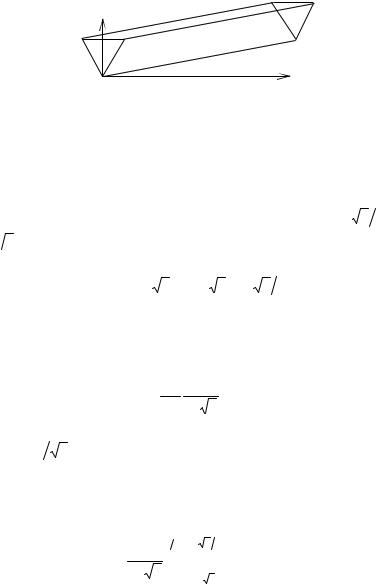
2.24. Поперечное сечение треугольной трубы со стороной а и принятая система координат показаны на рис. О9.

y

a

x

Рис. О9

Распределение скоростей по сечению трубы описывается уравнением (2.31)

∂2u

z

+

∂2u

z

= −

p

,

u

z

= 0 .

(2.24.1)

∂x2

∂y2

μ l

г

y = a 3 2 ,

Из уравнений прямых, образующих сечение канала

y = ± 3x , построим функцию, принимающую нулевые значения на

границах канала:
ω(x, y) = ( y − 3x)( y + 3x)(a 3 2 − y)	(2.24.2)
и решение для поля скорости ищем в виде,
uz (x, y) = Bω(x, y) .	(2.24.5)

Подставляя (2.24.5) в (2.24.1), находим, что уравнение (2.24.1)

удовлетворяется при
	B =	p 1	.	(2.24.6)
		μ l 2a	3
Максимум	скорости достигается		в центре	треугольника
( x = 0, y = a	3 ) и равен

umax =			1				pa			2
							μ l			.	(2.24.7)
			36
Средняя скорость определяется интегралом
a2	3	a 2					a	3 2
			∫					∫	uz (x, y)dy
u0 = 8					dx
			0				x		3
			92

u0 = 20 9 =

(2.24.8)

и равна

= 1 pa2 u0 80 μ l .

Отношение максимальной скорости к средней umax

= 2,22.

Соотношение (2.24.8) определяет связь перепада давления в канале p со средней скоростью u0 . Его можно переписать в виде

формулы Дарси (2.32) и определить коэффициент гидравлического сопротивления треугольной трубы.

	λтр =	A	,	A =	160	= 53,3 .	(2.24.9)
		Re			3

При определении (2.24.9) учтено, что гидравлический диаметр треугольной трубы равен dг = a3 , а число Рейнольдса определя-

ется как Re = u0νdг .

2.25. Так как течение жидкости в пленке установившееся, то поперечное движение отсутствует ux = uy = 0 , продольная скорость

изменяется только по толщине пленки uz ( y) , давление постоянно по толщине пленки ( ∂∂py = 0 ), при этом продольный градиент дав-

ления в пленке жидкости совпадает с градиентом в окружающей

среде	dp	= ρвg . Уравнение (2.10) для		продольной			компоненты
	dz
скорости упрощается к виду
		0 = g(ρ − ρв) + μ	d	2u	z	.	(2.25.1)
			dy2
На стенке выполняется условие прилипания
		uz ( y = 0) = 0 .					(2.25.2)

Пренебрежение трением пленки о воздух означает, что на поверхности пленки

93

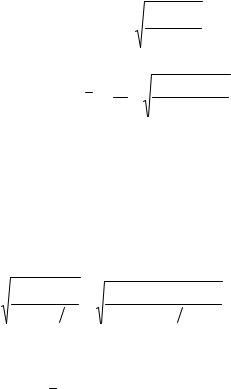
	duz	= 0 .	(2.25.3)
	dy
		y =δ

Интегрируя (2.25.1) при граничных условиях (2.25.2) и (2.25.3) находим распределение скорости по толщине пленки

	g(ρ−ρ	в	)			y
uz ( y) =				y	δ −		.
	μ					2

Расход жидкости на единицу ширины пленки

	δ	g(ρ−ρв)	δ3 ,
	Vl = ∫uz ( y)dy =
		3μ
	0

откуда толщина пленки

δ = 3 3Vl μ

g(ρ−ρв)

и средняя скорость

(2.25.4)

(2.25.5)

uz = Vl = 3 g(ρ − ρв)Vl 2 . (2.25.6)

δ3μ

2.26.Предполагаем, что режим течения в пленке ламинарный, а толщина пленки достаточно мала по сравнению с диаметром трубки, чтобы пленку можно считать плоской. Воспользуемся результатами, полученными при решении задачи 2.25.

Расход на единицу ширины стекающей пленки

V

V

22,6 10−3

−4

2

=

=

=1,00 10

м /с.

πd

3,6 103 π 20 10−3

l

Толщина пленки

δ = 3

3Vl

ν

ρ)

= 3

3 10−4 1,003 10−6

= 0,31 10−3 м

g(1−ρв

9,8(1−1,205 998,2)

( ν =1,003 10−6 м2/с, ρ = 998,2 кг/м3, ρв =1,205

кг/м3).

Средняя скорость

V

10−4

u

=

l

=

= 0,32 м/с.

0,31 10−3

δ

94

Кривизна пленки мала ( δ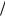d = 0,015), пленку можно считать плоской. Вычислим число Рейнольдса:

	Re =	u	4δ		=	0,32 4 0,31 10			−3
			ν			1,003 10−6			= 396 .
Режим течения ламинарный.
2.27. F = 18149 Н.
2.28. ν =	gd 4 τ			= 4,74 10			−6	2
								м /с.
	32 ln 2 D2l

2.29. Движение жидкости в зазоре между пластинами в предположении вязкостного режима течения и осевой симметрии поля скоростей имеют вид

1 ∂

(rur ) +

∂uz

= 0 ,

r ∂r

∂z

0

= −

1 ∂p

+

1 ∂

r

∂u

r +

∂2u

r

−

u

r

,

μ ∂r

r ∂r

r

∂r

∂z2

2

0 = −

1

∂p

+

1

∂

r

∂u

z

+

∂2u

z .

μ ∂z

r

∂r

∂r

∂z2

(2.29.1)

(2.29.2)

(2.29.3)

Тонкость слоя жидкости позволяет принять дополнительные упрощения. Из уравнения неразрывности следует, что осевая компонента скорости мала по сравнению с радиальной (их отношение пропорционально hr ). При этом из (2.29.2) и (2.29.3) получаем

∂∂pz << ∂∂pr , то есть изменением давления поперек слоя можно пре-

небречь и считать p = p(r, τ) . Тонкость слоя позволяет также по-

лагать, что изменения скорости поперек слоя более существенны, чем вдоль, при оценке сил трения в (2.29.2). Окончательно вместо

(2.29.2) и (2.29.3) имеем

0	= −	1	∂p				+	∂2u	r ,	(2.29.4)
		μ ∂r
								∂z2
	0 = −				1	∂p .				(2.29.5)
					μ ∂z
				95

Интегрируя уравнение неразрывности (2.29.1) по ширине слоя, находим

	1 ∂		(ruvrhh) + uz (z = h) = 0 ,	(2.29.6)
	r ∂r

1 h

где обозначено urh ≡ h ∫0 ur (z, r, τ)dz .

Осевая скорость на поверхности слоя равна скорости перемеще-

ния пластины uz (z = h) = dhdτ , которая не зависит от радиуса. Ин-

тегрируя (2.29.6) по радиусу, находим распределение средней по ширине слоя радиальной компоненты скорости

u	rh = −	1 dh	r	.	(2.29.7)
		h dτ 2

Обратимся к уравнению (2.29.4). Интегрирование его с учетом условия прилипания на поверхностях слоя дает распределение радиальной компоненты скорости по толщине слоя

ur = −	1	∂p z(h − z)	(2.29.8)
	2μ ∂r

и позволяет, интегрируя (2.29.8), связать среднюю по ширине слоя скорость с градиентом давления

u	rh = −	1	∂p h2 .	(2.29.9)
		12μ ∂r

Исключая из (2.29.7) и (2.29.9) среднюю скорость urh , получим

уравнение для давления			dh r ,
∂p	=	6μ		(2.29.10)
∂r
		h3 dτ

интегрирование которого при условии, что жидкость из слоя вы-

тесняется в среду с давлением			p0 , дает распределение давления в
виде			3μ dh
p = p		−			(r2	− r2 ) .	(2.29.11)
			h3 dτ
	0				0
			96

Прижимающая сила F , действующая на пластину, компенсируется суммарной силой избыточного давления на пластину со стороны жидкости в слое (массой пластины пренебрегаем)

r		3πμ3	dh r04 .
F = ∫0	( p − p0 )2π rdr = −			(2.29.12)
0		2h	dτ

Соотношение (2.29.12) представляет собою уравнение для определения h(τ) . Его решение

h(τ)			4		Fh2	τ)−0,5 .
	= (1	+			0		(2.29.13)
h			3π μ r4
0				0

2.30. Течение считаем вязкостным, кроме того, ввиду тонкости пленки жидкости используем приближения теории пограничного слоя, в частности, пренебрегаем изменением давления поперек пленки, то есть полагаем, что градиент давления в пленке равен

градиенту в окружающей среде (воздухе) ∂∂px = ρвg . Итоговая сис-

тема уравнений, описывающая движение пленки, включает уравнение неразрывности и уравнение для продольной компоненты скорости

∂u

x

+

∂uy

= 0

,

(2.30.1)

∂x

∂y

(ρ − ρв)g + μ

∂

2u

x

= 0 .

(2.30.2)

∂y2

Решение уравнения (2.30.2) при условии прилипания на стенке

ux ( y = 0) = 0 и условии отсутствия трения пленки о воздух
∂ux		= 0 дает распределение скорости в пленке
∂y
		y =δ

		(ρ−ρв)g			y
	ux ( y) =		y	δ −		.	(2.30.3)
		μ			2

Расход жидкости в пленке

97

	δ	(ρ −ρв)g	δ3 .
	V = ∫ux ( y)dy =			(2.30.4)
		3μ
	0

Интегрирование уравнения неразрывности по координате y , в пределах от нуля до δ, дает уравнение баланса массы для пленки

	∂V	+	∂δ	= 0 .	(2.30.5)
	∂x		∂τ

При записи (2.30.5) учтено, что uy ( y = δ) ≡ ∂∂δτ .

Подставляя в (2.30.5) выражение для расхода жидкости в пленке (2.30.4), получим основное уравнение, описывающее поведение пленки:

	(ρ − ρв)g	δ2 ∂δ	+	∂δ	= 0 .	(2.30.6)
	μ			∂τ
		∂x

Для решения (2.30.6) необходимо задать начальное условие: распределение толщины пленки по длине при τ = 0 и граничное

условие при x = 0 . В качестве последнего примем
δ(x = 0, τ) = 0 .	(2.30.7)

Для упрощения будем искать автомодельное по времени решение уравнения (2.30.6), которое устанавливается через некоторое время после начала процесса и не зависит от начального условия. При этом распределение толщины пленки по длине остается по-

добным самому себе при изменении времени и имеет вид
	δ(x,	τ) = f (x) T (τ) .				(2.30.8)
Подставляя (2.30.8) в (2.30.6), приходим к уравнениям
	(ρ −ρв)g	df	1		dT
		f dx	= −		dτ = m .	(2.30.9)
	μ			T 3

Первый член в (2.30.9) – функция только х, второй – функция τ, поэтому они порознь равны константе m , имеющей, как не трудно установить, положительное значение.

Решение уравнения для f (x) (2.30.9) с учетом граничного условия (2.30.7) дает

98

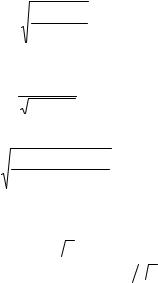
f (x) =	2μ m x .
	(ρ −ρв)g

Уравнение для T (τ) (2.30.9) приводит к

T (τ) =	1
	2mτ + c .

Для толщины пленки окончательно получаем

δ(x, τ) =		μ x		,
	(ρ −ρ	в	)g(τ + c )
			1

(2.30.10)

(2.30.11)

(2.30.12)

где c1 = c2m – константа интегрирования.

Согласно (2.30.12) толщина пленки нарастает по мере удаления от передней кромки пропорционально x и при больших временах утончается с течением времени пропорционально 1 τ .

Константу интегрирования c1 можно определить, если после

наступления автомодельного режима известно значение толщины пленки δ0 в момент τ0 на расстоянии x0 от передней кромки. В

этом случае

	с1 =			μ x0			− τ0 .		(2.30.13)
			(ρ −ρв)gδ02
Если в момент τ0 известна масса жидкости M 0									в пленке длиной
l
l ( M (τ) = ∫δ(x, τ) ), то
0
		2l		2	μ l
c1								− τ0 .	(2.30.14)
	=	3M0			(ρ −ρв)g

2.31. При заданных условиях для нестационарного поля скорости uϕ (r, τ) имеем задачу (см. (2.13))

1

∂uϕ

=

∂2uϕ

+

1 ∂uϕ

−

uϕ

,

(2.31.1)

ν

∂τ

∂r2

r

∂r

r2

99

uϕ(r, τ = 0) = 0 ,

(2.31.2)

uϕ(r = r0 , τ) = u0 ≡ ω r0 .

(2.31.3)

При τ → ∞ согласно 2.18 в жидкости устанавливается профиль

скорости

r

uϕ(r) = u0

.

(2.31.4)

r

0

Будем искать решение в виде

r

uϕ(r, τ) = u0

−uϕ1(r,

τ) .

(2.31.5)

r

0

При этом для uϕ1 (r, τ)

получаем задачу с однородным гранич-

ным условием

1 ∂uϕ1

=

∂2uϕ1

+

1 ∂uϕ1

−

uϕ1

,

(2.31.6)

ν

∂τ

∂r 2

r ∂r

r 2

uϕ1(r, τ = 0) = u0

r

,

(2.31.7)

r

0

uϕ(r = r0 , τ) = 0 ,

(2.31.8)

которая решатся методом разделения переменных.

Окончательно получаем

r

∞

2 ν τ

r

, (2.31.9)

uϕ(r, τ) = u0 r

∑Ck exp

− μk r

2

J1

μk

r

0 k =1

0

0

1

∫J1 (μk ξ)ξ2dξ

C

k

= u

0

0

, μ

k

–

корни уравнения J

1

(μ) = 0 .

1

∫J12 (μk ξ)ξdξ

0

МЕТОДЫ РАЗМЕРНОСТЕЙ И ПОДОБИЯ

3.1.p = f (ρuμ0d ) dl ρ u02 . Полученное соотношение представ-

ляет частный случай формулы Дарси (2.32).

100