Корсун Гидродинамика ЯЕУ Сборник задач и упражнений 2008

жидкости u0, давление p0, плотность жидкости ρ. Определить результирующую силу, действующую на цилиндр.

1.15.Определить потенциал поля скорости ϕ(x, y, z) прямоли-

нейного поступательного потока со скоростью u0 в направлении единичного вектора n .

1.16.Определить потенциал поля скорости ϕ(x, y) и функцию

тока Ψ(x, y) плоского прямолинейного поступательного потока со скоростью u0 в направлении единичного вектора n .

1.17. Построить потенциал поля скорости ϕ(x, y, z) источника

(стока) мощностью Q [м3/с], действующего в начале координат. То же для источника в произвольной точке rr0 .

1.18. Построить потенциал поля скорости ϕ(x, y) и функцию тока Ψ(x, y) линейного источника (стока) мощностью V [м2/с], действующего в начале координат. То же для источника в произвольной точке rr0 .

1.19. Построить потенциал поля скорости ϕ(x, y) и функцию тока Ψ(x, y) плоского потенциального вихря с циркуляцией Г с

центром в начале координат (плоский потенциальный вихрь – круговое движение жидкости, линии тока которого представляют окружности с центром в начале координат). То же для вихря с центром в произвольной точке r0 .

1.20. Комплексный потенциал плоского течения равен Φ = az . Определить потенциал, функцию тока и поле скоростей течения.

1.21. Показать, что комплексный потенциал Φ(z) = u∞(z + r02 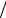z) , представляющий сумму комплексных потенциалов потока со скоростью u∞ и плоского диполя с моментом M = 2πu∞r02 , определяет поле скоростей в потоке, поперечно обтекающем цилиндр радиусом r0.

1.22. Показать, что комплексный потенциал Φ(z) = czn , где c и

n – действительные числа и n > 1, описывает течение внутри угла равного π / n.

11

2. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ

ОСНОВНЫЕ ПОПЛОЖЕНИЯ

Уравнения движения

Уравнение импульсов для любой сплошной среды имеет вид

		∂u		∂u		∂Pji
	ρ	i + ρu		i	= ρP +		,	i =1, 2, 3 ,	(2.1)
			j ∂xj			∂xj
		∂τ			Vi
	где PVi – компоненты вектора плотности объемной силы,								Pij –

компоненты тензора напряжений поверхностной силы, по повторяющемуся индексу проводится суммирование от 1 до 3.

Для ньютоновской жидкости напряжения в потоке равны

		2	r			∂u	i		∂u j
P	= −( p +		μ div u)δ		+μ			+		.	(2.2)
		3				∂x			∂x
ij				ij			j
									i

Уравнения импульсов (2.1), (2.2) вместе с уравнением сохранения вещества (1.1), уравнением состояния (1.3) и уравнением сохранения энергии (теплопереноса), которое имеет вид

ρc

∂T

+ρc

u

∂T

=

∂

λ

∂T

+ q

+

∂p

+u

∂p

+μD , (2.3)

p ∂τ

∂x j

∂x j

p

j ∂x j

V

∂τ

j ∂x j

образуют замкнутую систему уравнений, описывающую движение вязкой (ньютоновской) жидкости. Последний член в (2.3) учитывает тепловыделение, обусловленное работой, совершаемой потоком против сил вязкого трения. Диссипативная функция D определяется полем скоростей движения жидкости

		∂ui			∂u j		∂u j		2	(div ur)2 .
	D =			+				−			(2.4)
					∂x		∂x		3
		∂x	j
					i		i

Член qV учитывает тепловыделение в потоке не связанное с движением жидкости.

12

Движение жидкости с постоянными свойствами, когда

ρ = const и μ = const , описывается системой уравнений в вектор-

ном виде	div u = 0 ,				(2.5)
∂ur
	+ (ur )ur = Pr	−	1 grad p + ν 2ur	,	(2.6)
∂τ	V		ρ

или в полной записи в прямоугольной декартовойсистеме координат

∂u

x

+

∂uy

+

∂u

z

= 0 ,

(2.7)

∂x

∂y

∂z

∂ux

∂ux

∂ux

∂ux

1

∂p

2

2

2

+ux

+uy

+uz

= gx

−

∂ ux

+

∂ ux

+

∂ ux

,

(2.8)

∂τ

∂x

∂y

∂z

ρ

∂x

+ν

∂x

2

∂y

2

∂z

2

∂uy

∂uy

∂uy

∂uy

1 ∂p

2

2

2

+ux

+uy

+uz

= gy −

∂ uy

∂ uy

∂ uy

,

(2.9)

∂y

+ν

+

+

∂τ

∂x

∂y

∂z

ρ

∂x2

∂y2

∂z2

∂u

∂u

∂u

∂u

= g

−

1 ∂p

∂2u

+

∂2u

+

∂2u

z

(2.10)

z +u

x

z +u

y

z +u

z

z

+ν

z

z

.

∂τ

∂x

∂y

z

∂z

ρ ∂z

∂x

2

∂y

2

∂z

2

Вкачестве объемной силы в (2.8) – (2.10) записана сила тяже-

сти.

Вцилиндрической системе координат (r, φ, z) уравнения движения жидкости с постоянными физическими свойствами имеют вид

1 ∂

(rur ) +

1 ∂uϕ

+

∂u

z

= 0

,

(2.11)

r ∂r

r ∂ϕ

∂z

∂u

r

+ur

∂u

r

+

uϕ

∂u

r

+uz

∂u

r

−

uϕ2

=

r

r

∂τ

∂r

∂ϕ

∂z

(2.12)

1

∂p

ur

2

∂u

2

ϕ

= gr −

ur

+ ν

−

−

,

ρ

∂r

r

2

r

2

∂ϕ

∂uϕ

+ur

∂uϕ

+

uϕ

∂uϕ

+uz

∂uϕ

+

uruϕ

=

∂τ

∂r

r

∂ϕ

∂z

r

(2.13)

1

∂p

u

2

ϕ

= gϕ −

2

uϕ −

∂ur

2

+

rρ ∂ϕ

+ν

r

r

2

∂ϕ

,

13

∂u

z

+ur

∂u

z

+

uϕ ∂u

z

+uz

∂u

z

= gz

−

1

∂p

+ ν 2uz ,

(2.14)

∂τ

r

∂ϕ

∂z

ρ ∂z

∂r

2 ≡

1 ∂

r

∂

+

1 ∂2

+

∂2

.

r ∂r

∂r

r2 ∂ϕ2

∂z2

Те же уравнения в сферической системе координат ( r,

ϕ,

ϑ )

1

∂

(r

2

ur ) +

1

∂uϕ

+

1

∂

(uϑ sin ϑ) = 0 ,

(2.15)

r2 ∂r

r sin ϑ ∂ϕ

r sin ϑ ∂ϑ

∂u

r

+ur

∂u

r

+

uϕ

∂u

r +

u

ϑ

∂u

r

−

uϕ2

+uϑ2

= gr −

1

∂p

+

r

r

ρ ∂r

∂τ

∂r

sin ϑ ∂ϕ

r

∂ϑ

+ ν( 2u

r

−

2u

r

−

2 ∂u

ϑ

−

2

u

ϑ

ctgϑ−

2

∂uϕ

) ,

(2.16)

r

2 ∂ϑ

r2

r2 sin ϑ ∂ϕ

r2

∂uϕ

+ur

∂uϕ

+

uϕ

∂uϕ

+

uϑ ∂uϕ

+

uϕur

+

uϕuϑ ctgϑ

=

∂τ

∂r

r sin ϑ ∂ϕ

r

∂ϑ

r

r

= gϕ −

1

∂p

+

rρsin ϑ ∂ϕ

(2.17)

2

u

ϕ

2

∂ur

2cos ϑ ∂uϑ

uϕ

+

ν

−

+

+

,

r

2

sin

2

ϑ

r

2

sin ϑ ∂ϕ

r

2

sin

2

ϑ

∂ϕ

∂u

∂u

uϕ

∂u

u

ϑ

∂u

u

u

ϑ

uϕ2ctgϑ

ϑ

+ur

ϑ

+

ϑ

+

ϑ

+

r

−

=

r

r

r

r

∂τ

∂r

sin ϑ ∂ϕ

∂ϑ

= gϑ −

1

∂p

+

rρ ∂ϑ

(2.18)

2

∂u

u

2 cos ϑ ∂uϕ

2

r

ϑ

uϑ

+

2

−

2

2

−

2

2

+ ν

r

∂ϑ

r

sin

ϑ

sin

ϑ ∂ϕ

,

r

где обозначено

2

1

∂

2

∂

1

∂

∂

1

∂2

=

r

+

sin

ϑ

+

.

r

2

∂r

∂r

r

2 sin

ϑ ∂ϑ

∂ϑ

r

2 sin 2

ϑ ∂ϕ2

14

Внешнее обтекание тел. Ламинарный пограничный слой

Число Рейнольдса является мерой отношения конвективных сил инерции в потоке к силам вязкого трения. При малых значениях числа Рейнольдса, составленного по скорости набегающего потока и характерному размеру обтекаемого тела, реализуется вязкостное (ползущее) течение – движение жидкости, при котором конвективные силы инерции в потоке малы по сравнению с силами вязкого трения.

Опуская в (2.6) член (u )u , учитывающий конвективные силы

инерции, для вязкостного течения имеем
∂ur		div u = 0 ,	(2.19)
	= Pr	− 1 grad p + ν 2ur .	(2.20)
∂τ	V	ρ

Уравнения вязкостного течения линейны относительно скорости. Как следствие, сила, действующая на тело при обтекании его потоком жидкости, при малых значениях числа Рейнольдса оказывается пропорциональна скорости потока.

При больших значениях числа Рейнольдса конвективные силы инерции велики по сравнению с силами вязкого трения везде, кро-

ме области вблизи поверхности обтекаемого тела. Из-за условия прилипания на стенке с ростом скорости набегающего потока увеличиваются и градиенты скорости на стенке, т.е. растут силы трения в пристенной области, оставаясь сравнимыми по величине с силами инерции.

Таким образом при больших значениях числа Рейнольдса поток можно разбить на две области: пограничный слой – пристенная область, в которой конвективные силы инерции и силы вязкого трения одинаковы по порядку величины и в которой сосредоточено основное изменение скорости, и внешний поток – область за пределами пограничного слоя, в которой силы вязкого трения не существенны и поле скоростей описывается уравнениями движения невязкой жидкости (1.1)–(1.3).

15

С увеличением скорости набегающего потока толщина пограничного слоя уменьшается обратно пропорционально корню из скорости. Тонкость пограничного слоя позволяет упростить уравнения, описывающие поле скоростей в пристенной области. Согласно Прандтлю система уравнений для течения в пограничном

слое при обтекании плоской пластины ( y = 0, x > 0) имеет вид

∂ρu

x

+

∂ρuy

= 0 ,

(2.21)

∂x

∂y

ρux

∂ux

+ρuy

∂ux

= − dp

+

∂

μ

∂ux

.

(2.22)

∂y

∂y

∂x

dx

∂y

Продольный градиент давления в потоке при этом определяется изменением скорости за пределами пограничного слоя

− dp	= ρu0	du0	.	(2.23)
dx		dx

В отсутствии градиента давления решение системы (2.21), (2.22) дает для трения на стенке в зависимости от расстояния от передней кромки пластины

	τст(x) = c f (Rex )		ρu2	,			(2.24)
			0
	где коэффициент трения равен		2
					u0 x
	c f (Rex ) =	0,664 , Rex		=		.	(2.25)
		Rex			ν

Система уравнений (2.21), (2.22) описывает асимптотический пограничный слой. Если принять, что пограничный слой имеет конечную толщину δ(x) и продольная скорость изменяется автомодельно, т.е.

ux (x, y)	= F(	y
			) ,	(2.26)
u0		δ(x)

то для толщины пограничного слоя можно получить

δ(x) = kδ	ν x .	(2.27)
	u0

16

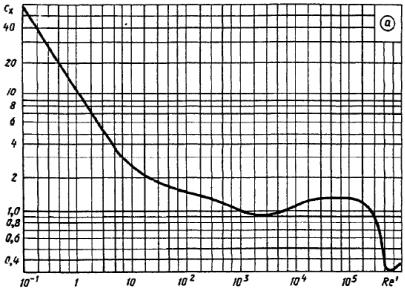
В частности, при аппроксимации поля скорости функцией F(Y ) = 2Y − 2Y 3 +Y 4 коэффициент kδ равен kδ = 5,83.

При обтекании тел произвольной формы неограниченным потоком жидкости сила лобового сопротивления может быть представлена в виде

F	= C		(Re)	ρu	2	S		,	(2.28)
		D		2	0
лс							м
где u0 – скорость набегающего потока,						Sм			– миделево сечение те-

ла (площадь тела на «просвет» со стороны потока), CD (Re) – коэффициент лобового сопротивления тела, зависящий от числа Рейнольдса, Re = u0l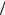ν, l – характерный размер тела.

Зависимость коэффициента лобового сопротивления от числа Рейнольдса при обтекании шара приведена на рис. 2.1 и при поперечном обтекании цилиндра – на рис. 2.2.

Рис. 2.1

17

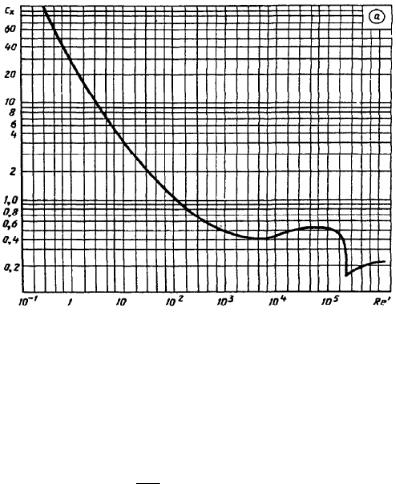
Рис. 2.2

Слоистые течения жидкости. Ламинарное движение жидкости в трубах и каналах

Слоистыми течениями называют течения, в которых отлична от нуля только одна компонента скорости. Если это компонента uz , т.е. ux = uy = 0, то из уравнения неразрывности для несжимаемой

жидкости (1.1) следует ∂∂uzz = 0 , а значит uz = uz (x, y, τ) . В отсутст-

вии массовых сил уравнения движения для слоистых течений имеют вид:

ρ

∂u

z

= −

∂p

∂2u

z +

∂2u

,

(2.29)

+μ

z

∂τ

∂z

∂x

2

∂y

2

∂p

= ∂p

= 0 .

(2.30)

∂x

∂y

18

Частным случаем слоистого течения является стационарное, установившееся (т.е. вдали от входа) движение жидкости в прямых каналах произвольного поперечного сечения. При этом

∂∂pz = const = − lp , где p – перепад давления на длине канала l.

Уравнение описывающее распределение скорости uz (x, y) по сечению канала

∂2u	z +	∂2u	z	= −	p	(2.31)
					μ l
∂x2		∂y2

решается с условием прилипания на стенках канала uz Г = 0 .

Перепад давления при движении жидкости в каналах связан со средней скоростью жидкости в канале u0 и его длиной l формулой

	Дарси:
			l		2
		Ψм + λтр(Re)			ρu0	.	(2.32)
	p =				2
			dг

В соотношении (2.32): λтр(Re) – коэффициент гидравлического сопротивления установившегося течения, зависящий от числа Рей-

нольдса Re = u0νdг , Ψм – коэффициент местных сопротивлений,

учитывающий отличие распределение скорости в канале от установившегося, обусловленное различными причинами (вход в канал, поворот, шайба, вентиль и т.п.), dг – гидравлический диаметр ка-

нала, dг = 4S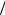П , где S – площадь проходного сечения канала, П – смоченный периметр.

При ламинарном течении жидкости в каналах λтр = А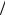Re , где коэффициент A зависит от формы поперечного сечения канала.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Как напряжения в потоке вязкой жидкости связаны с полем скорости?

2.Что такое вязкостное течение? Приведите пример.

19

3.Как можно упростить задачу, если при обтекании сферы потоком жидкости оказалось, что число Рейнольдса мало (велико)?

4.Что такое пограничный слой? Когда можно говорить о существовании пограничного слоя?

5.В пограничном слое силы инерции и силы вязкости одинаковы по порядку величины. А за его пределами?

6.Как толщина пограничного слоя на плоской пластине зависит от расстояния от передней кромки пластины?

7.Как касательное напряжение на стенке при продольном обтекании пластины потоком жидкости зависит от расстояния от передней кромки?

8.Как коэффициент гидравлического сопротивления зависит от числа Рейнольдса приламинарномтечении жидкости в трубах?

ЗАДАЧИ И УПРАЖНЕНИЯ

2.1. Определить поле скоростей и давлений при вязкостном обтекании неограниченным потоком жидкости шара радиусом r0 .

Вдали от шара скорость жидкости u0 и давление p∞ . Определить

силу, действующую на шар, и коэффициент лобового сопротивления шара.

2.2.Определить скорость падения водяных капель в воздухе вблизи поверхности земли. Диаметр капель принять 0,01, 0,03, 0,10

и0,30 мм. То же для градин диаметром 3 и 6 мм.

2.3.Определить установившуюся скорость движения капель расплава свинца в жидком натрии под действием сил тяжести. Кап-

ли расплава свинца принять в виде шариков диметром 4 мм. Плотность свинца 10500 кг/м3, натрия 830 кг/м3, динамическая вязкость натрия 2,9·10-7 м2/с.

2.4.Оценить коэффициент динамической вязкости глицерина с плотностью 1250 кг/м3 , если стальной шарик диаметром 3 мм,

опущенный в сосуд с глицерином, достиг дна сосуда через 8,0±0,2 с. Высота уровня глицерина в сосуде 300 мм.

2.5. Оценить скорость свободного падения парашютиста. Руки, ноги, туловище моделировать как отрезки цилиндров.

20