Корсун Гидродинамика ЯЕУ Сборник задач и упражнений 2008

4.ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ

ВКАНАЛАХ ЯЭУ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Турбулентное движение жидкости предполагает наличие неупорядоченности течения, в котором различные величины претерпевают хаотическое изменение по времени и пространственным координатам и при этом могут быть выделены статистически точные их средние значения.

Турбулентное движение можно считать суперпозицией вихрей с различными размерами и завихренностью, имеющими определенные верхний и нижний пределы.

При турбулентном режиме течения мгновенные значения гидродинамических параметров (компонент скорости, давления, температуры и др.), могут быть представлены в виде суммы осредненной во времени величины и её пульсационной составляющей. Например, полная мгновенная скорость потока определяется в виде

разложения: ur = ur +ur′, где u −мгновенное значение скорости; ur

– её среднее значение; u′ – пульсационная составляющая скорости.

Предполагается, что поле мгновенных скоростей и давлений при турбулентном движении описывается уравнениями Навье–Стокса. Уравнения для средних значений скоростей и давлений в турбулентных потоках получаются путем осреднения уравнений Навье– Стокса по времени и носят название дифференциальных уравнений Рейнольдса средних скоростей и давлений. Для несжимаемой жидкости они имеют вид

∂ ρ

∂ ρ

∂

∂

∂

uiu j

P

u

u

i

i +

= −

+

μ

− ρu'u'

, (4.1)

∂ τ

∂ x

∂ x

∂ x

∂ x

j

j

i j

i

j

где −ρui'u'j – компоненты тензора турбулентных напряжений (или

напряжений Рейнольдса). Диагональные члены (при i = j) являются нормальными турбулентными напряжениями и характеризуют

41

турбулентное давление, недиагональные члены (при i = j) – турбулентные касательные напряжения.

Вид выражений (4.1) подразумевает суммирование по повторяющемуся индексу и используется для записи сразу трех проекций дифференциальных уравнений.

Уравнение неразрывности для турбулентного потока несжимаемой жидкости имеет вид:

	∂ ρ		j
		u		= 0 .	(4.2)
	∂ x j

Из-за появления членов −ρui'u'j , учитывающих дополнительный

перенос импульса за счет турбулентных пульсаций, система уравнений (4.1)–(4.2) является разомкнутой.

Для замыкания системы уравнений движения (4.1) и неразрывности (4.2) используются различные полуэмпирические модели, наиболее известной из которых является модель Прандтля.

Согласно этой модели выражения для турбулентных касательных напряжений PxyT при прямолинейном течении жидкости в направлении оси x имеют вид:

T

d

u

x

'

'

' '

P

= −ρu

u

= ρl u

.

(4.3)

dy

xy

i

j

y

Всоответствии с гипотезой Ж. Буссинеска (1877 г.) по аналогии

смолекулярным вязким напряжением μ = ρVl , ( μ – коэффициент

молекулярной динамической вязкости, ρ – плотность, V – средне-

квадратичная скорость молекул, l – средняя длина свободного пробега) в формуле (4.3) можно выделить турбулентную вязкость:

μt = ρu'yl' .			(4.4)

Использование предположения о равенстве по порядку величины поперечной и продольной пульсаций скорости

du

x

u'

≈

u'

≈

l'

приводит к следующему выражению для ком-

y

x

dy

понент турбулентных касательных напряжений:

42

PT

≈

d

u

x

d

u

x

= ρl2

d

u

x

d

u

x

,

ρl'2

(4.5)

xy

dy

dy

dy

dy

где величину l = l'2 принято называть длиной пути перемешива-

ния (длиной пути смешения Прандтля); l характеризует локальные свойства турбулентного потока и может рассматриваться как пространственный масштаб турбулентности.

Прандтль предположил, что длина пути перемешивания возрастает линейно по мере удаления от стенки:

l = χ y ,

(4.6)

что и было подтверждено экспериментально в опытах Никурадзе и других авторов. По данным измерений константа турбулентности

χ= 0,4.

Для плоского прямолинейного течения жидкости выражение для турбулентной вязкости имеет вид:

	μt = ρl2	d	u	x		.	(4.7)
		dy

В случае обтекания плоскости прямолинейным потоком, направленным вдоль оси x, система дифференциальных уравнений Рейнольдса (4.1) сводится к уравнению:

∂

∂

d

P

u

−

+

(μ

x

− ρu'u'

) = 0 ,

(4.8)

∂x

∂y dy

i j

которое описывает распределение осредненной скорости.

В безградиентном потоке (при ∂∂Px = 0 ) касательное напряже-

ние не меняется по поперечной координате y и равно касательному напряжению на стенке:

	d
		u
μ			x	−ρu'u'		= τ	ст	= const .	(4.9)
	dy				i j

Из (4.9) следует, что в пристенной области потока распределение скорости зависит от ux = f ( y, ν, τст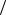ρ) или в безразмерном виде

43

						yu
		u	x
				=	f	*	,	(4.10)
	u*					ν

где u* =	τст ρ	– динамическая скорость или скорость трения на
стенке.	универсальные координаты: ϕ = ux u* – безразмерную
Вводя
скорость и η =		yu*	– безразмерное расстояние от стенки, получим,
		ν

что при τст = const в пристенной области распределение скоростей

для различных τст, ν	описывается единой зависимостью,	полу-
чившей название универсального профиля скорости:
	ϕ = ϕ(η) .	(4.11)
Вид функции ϕ(η)	меняется в зависимости от безразмерного

расстояния до стенки η.

В модели Прандтля принимается простейшее допущение о полном отсутствии турбулентного переноса в узкой пристеночной области, где основную роль играют силы молекулярной вязкости. В

этой области, называемой вязким подслоем, при	η< ηв имеет ме-
сто линейное распределение скорости
ϕ = η .	(4.12)

По мере удаления от стенки в турбулентной зоне пристеночной области определяющими становятся турбулентные напряжения. В

области развитой турбулентности при η > ηt закон распределения

скорости становится не зависящим от молекулярной вязкости, а распределение скорости описывается логарифмической зависимостью

ϕ =	1	ln η+ C .	(4.13)
	χ

Из экспериментов получено: ηв ≈ 5, ηt ≈ 30 , С = 5,5, а для количественных расчетов наибольшую популярность приобрели:

- двухслойная модель Прандтля:	η <11,7 ,
ϕ = η ;
ϕ = 2,5ln η+ 5,5 ;	η ≥11,7 ,	(4.14)

44

- трехслойная модель Кармана:

ϕ = η;	η < 5 – вязкий подслой,
ϕ = 4,92ln η+ 3,06 ;	5 ≤ η≤ 30 – промежуточный слой, (4.15)
ϕ = 2,5ln η+ 5,5 ;	η > 30 – турбулентное ядро.

В отличие от ламинарного турбулентный пограничный слой

нарастает более энергично
δ = 0,3x	u*	.	(4.16)
	u0

Пристеночная область составляет всего 0,2 толщины турбулентного пограничного слоя, однако в ней порождается 75% всей пульсационной энергии и только 25% энергии турбулентных пульсаций возникает в остальных 0,8 толщины турбулентного пограничного слоя.

Распределение скорости по толщине турбулентного пограничного слоя определяется с учетом поправки на перемежаемость как

yu

y

u

x

= f

*

+ H f

,

(4.17)

u

ν

1

δ

*

yu

где

f

*

= f (η)

– универсальный профиль,

ν

f

=1 + sin π

(2

y

−1) ;

1

2

δ

Н = 1,375 – для пограничного слоя на плоской пластине.

Для расчета касательного напряжения на стенке используется

зависимость:
	τст = C f (Rex )	ρu	2	(4.18)
		2	0 ,
где C f (Rex )
	– коэффициент трения пограничного слоя, зависящий

от числа Рейнольдса Rex = uν0 x .

Для турбулентного пограничного слоя используются зависимости:

45

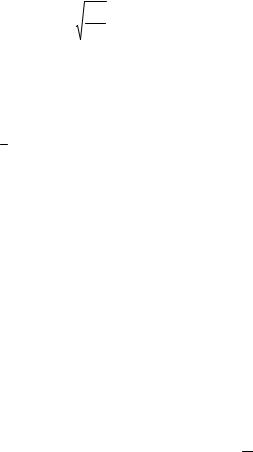
	C f = 0,0576Re−x	0,2 , 5 1055 < Rex <107 ,			(4.19)
	C f = 0,0262Re−x1/ 7 ,		Rex <109 ,		(4.20)
	δ = 0,3x		C f	.	(4.21)
			2

Распределение скорости в круглом канале можно получить, зная касательное напряжение на стенке τст и распределение турбулент-

ной вязкости μt ( y) ( y = R − r – расстояние от стенки; диус канала и текущий радиус):

u	x ( y) = y	τст(1− y / R)		dy .
	∫	μ +μ	( y)
0		t

В канале можно выделить 3 области:

1)вязкий подслой, где μ >> μt ,

2)переходную область, где μ ≈ μt ,

3)турбулентное ядро, где μ << μt .

R, r – ра-

(4.22)

Универсальный профиль скорости может быть использован в пристенной области для турбулентного течения, так как в области большого градиента скорости у стенки можно считать, что τ( y) ≈ τст = const , а в ядре потока профиль скорости меняется сла-

бо.

Для расчета гидравлического сопротивления канала используется обобщенная формула Дарси

				l		ρu	2
P =	Ψ + λ		(Re)			2	0	,	(4.23)
	м	тр		d

где Ψм – коэффициент местных сопротивлений, Ψтр ≡ λтр(Re) dl –

коэффициент сопротивления трения, λтр(Re) – коэффициент гид-

равлического сопротивления канала, зависящий от числа Рейнольдса:

	u2		8τ	ст
λтр =8	*	=			.	(4.24)
	u02		ρu02

46

На практике для определения λтр при движении жидкости в

круглых трубах наиболее часто используют эмпирическую формулу Блазиуса:

	λтр(Re) =		0,316			при	Re ≤105	(4.25)
				Re0,25
	и формулу Никурадзе:
			0,221
	λтр(Re) = 0,0032 +					при	105 < Re <108 .	(4.26)
		Re0,237

Для турбулентных режимов может быть также использована

	формула с учетом шероховатости стенок канала				:
			0,68	0,25
	λтр( , Re) = 0,11	+			,	(4.27)
			Re
	d

при	→ 0
	λтр(Re) →	0,316	.
		Re0,25

В практике инженерных расчетов сопротивления при движении жидкости в каналах некруглого поперечного сечения часто используется «метод эквивалентной трубы». При этом расчет проводится по формулам для круглых труб (4.23), (4,25) – (4.27) с использованием в качестве характерного размера гидравлического диаметра

	канала dг , равного
	dг =	4F	,	(4.28)
		П

где F – площадь поперечного сечения канала, П – смоченный периметр.

К.Д. Воскресенский показал, что для применения «метода эквивалентной трубы» необходимо выполнение во всех точках периметра канала неравенств

δu n, δu R ,

(4.29)

где n – расстояние по нормали к периметру до пересечения с противоположной стороной периметра, R радиус кривизны периметра канала, δu – толщина пристенного слоя жидкости, в котором

47

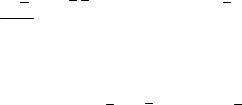
сосредоточено основное изменение скорости. Для оценки толщины δu получено соотношение

	δu =	8dг	.	(4.30)
		λтр(Re) Re

«Метод эквивалентной трубы» неприменим для каналов, имеющих особенности в виде значительных угловых зон (плотные упаковки стержней и т.п.). Расчет течения жидкости в подобных каналах, а также в каналах с переменной площадью проходного сечения проводится путем решения непосредственно уравнений Рейнольдса, в которых для определения компонент тензора турбулентных напряжений используются модели турбулентности. Простейшей двухпараметрической моделью является ( k − ε )-модель турбулентности.

Двухпараметрическая диссипативная (k – ε)-модель турбулентности

Система уравнений для расчета турбулентных течений на основе диссипативной двухпараметрической ( k − ε )-модели турбулентности включает в себя уравнение неразрывности (4.31), уравнения Рейнольдса (4.32), уравнения для кинетической энергии турбулентных пульсаций k (4.33) и скорости ее диссипации ε (4.34) :

∂ρui

∂τ

∂ ρ

j

u

= 0 ,

(4.31)

∂ x j

∂ ρ

u

u

∂

∂

∂

u

i

j

P

i

+

= −

+

μ

− ρu

' u '

,

(4.32)

∂ x

∂ x

∂ x

∂ x

j

i

j

j

i

j

∂ k

∂ k

∂

μt

∂ k

+u j

=

μ +

+

∂ τ

∂ x j

∂ x j

∂ x j

σk

(4.33)

∂

u

∂

u

2

∂

u

i

j

i

+ μ

+

−

δ

k

−ρε,

∂ x

3

∂ x

t

j

∂ x

ij

j

i

48

∂ ε

∂ ε

∂

μ

∂ ε

+u j

=

μ +

t

+

∂ τ

∂ x j

∂ x j

∂ x j

σε

ε

∂

u

i

∂

u

j

2

∂

u

i

+C

μ

+

−

δ

k

− ,

k

∂ x

∂ x

3

∂ x

ε1

t

j

ij

j

i

ρε2

∂2

u

2

i

−C

+C

νμ

.

k

∂ x

∂ x

ε2

ε3

t

k

j

где Cε1,Cε2 ,Cε3 ,σk ,σε – эмпирические коэффициенты, Кронекера.

(4.34)

δij – символ

Вмоделях турбулентные (рейнольдсовы) напряжения − ρui′ u′j

вуравнениях (4.32) связаны с полем скоростей деформаций осредненного потока посредством турбулентной вязкости μt соотноше-

ниями

∂

u

i

∂

u

j

2

−ρui′ u′j

= μt

∂ x

j

+ ∂ x

−

3 ρδij k .

(4.35)

i

При этом используется гипотеза, что турбулентную вязкость μt

можно представить в виде скаляра, величина которого определяется выражением:

	μ	t	= C	ρ	k 2	,	(4.36)
					ε
			μ

где Cμ – эмпирический коэффициент.

Хотя в определении эмпирических замыкающих коэффициентов Cμ,Cε1,Cε2 ,Cε3, σk ,σε , входящих в постановочные уравнения

(4.28)–(4.33) различных диссипативных моделей турбулентности, существуют некоторые различия, здесь можно привести их типичный набор, полученный с введением пристеночных функций, учитывающих уменьшение масштаба турбулентности при приближении к стенке:

C = 0,09exp[−3,4 /(1 + Re		/ 50)2 ] ,	C	=1,44 ,
μ	t		ε1
	49

Cε2 =1,92(1 − 0,3exp(−Ret 2 )) , Cε3 = 2,0 , σk =1,0 , σε =1,3 ,

где Ret = k 2 / νε – турбулентное число Рейнольдса.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Дифференциальные уравнения Рейнольдса. Как они получе-

ны?

2.Какой смысл имеют диагональные и недиагональные компоненты тензора турбулентных напряжений Рейнольдса?

3.Запишите универсальный профиль скорости. Какое он находит практическое применение?

4.Что такое u ?

5.Какие аппроксимации универсального профиля Вам извест-

ны?

6.Нарисуйте распределение скорости по радиусу трубы при ламинарном и турбулентном течении.

7.Как изменяется по радиусу трубы коэффициент турбулентной вязкости?

8.Как изменяется давление по длине трубы на участке стабилизированного течения при ламинарном режиме движения и турбулентном?

9.Как изменится перепад давления на участке трубы длиной l в области стабилизированного течения, если скорость увеличится вдвое? Режим течения а) ламинарный, б) турбулентный.

10.Нарисуйте зависимость коэффициента гидравлического сопротивления от числа Рейнольдса.

11.Как толщина вязкого подслоя зависит от числа Рейнольдса?

12.Чем определяется шероховатость трубы? Что означают понятия: гидравлически гладкая труба, абсолютно шероховатая труба?

13.При выполнении каких условий расчет сопротивления некруглого канала можно вести по формулам для круглых труб?

50