Крючков Теория переноса нейтронов 2007

VЦ = AV+11 .

Очевидны следующие выражения, определяющие переход от системы ЦМ к ЛС:

V	= V	+ V	,
r2	a	r ЦМ	(3.2)
VЦМ = −VЦ.

Связь скоростей и углов рассеяния в различных системах приведена на диаграмме скоростей (рис. 3.5).

B C

Va V2

ψ

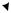Θ

ОA

VЦМ

Рис. 3.5. Диаграмма скоростей

Возведем обе части первого выражения (3.2) в квадрат:

V22 = (Vra + VrЦМ )2 ,

V22 = Va2 + VЦМ2 + 2 Va VЦМ cosψ.

91

Учитывая следующие соотношения

V

= V

−V

= V −

V1

= V

A

;

V

= V

1

,

a

1

Ц

1

A +1

1 A +1

ЦМ

1 A +1

перепишем последнее выражение в виде

V2 = V2

A2

+ V2

1

+ 2 V2

A

cos ψ .

(3.3)

1)2

2

1 (A +1)2

1 (A +

1 (A +1)2

Приведенная атомная масса нейтрона равна единице, следова-

	тельно, его кинетическая энергия записывается как E =									V2	. Под-
										2
	ставим это выражение в (3.3):
	E		= E	A2	+ E	1	+ 2 E	A	cosψ .
				(A +1)2		(A +1)2		(A +1)2
		2	1		1		1

Таким образом, получаем искомую связь энергии нейтрона до (Е1) и после (Е2) рассеяния:

E	2	= E	A2	+ 2 Acos ψ +1		.	(3.4)
		1		(A +1)2

Рассмотрим два предельных случая.

1. Если угол рассеяния в системе ЦМ равен нулю ( ψ = 0 ), что соответствует случаю отсутствия рассеяния, то cos ψ =1 и, следовательно, из формулы (3.4):

E		= E	A2 + 2A +1		= E .
			(A +1)2
	2	1			1

Таким образом, получен очевидный результат: если не было столкновения нейтрона с ядром, то его кинетическая энергия не изменилась.

92

2. Если угол рассеяния в системе ЦМ равен π ( ψ = π ), что соответствует рассеянию нейтрона «прямо назад», то cos ψ = −1, и, следовательно, из формулы (3.4):

A2 − 2A +1

A −1

2

E

= E

= E

≡ E α ,

(A +1)2

2

1

1

A +1

1

A −1

2

где α =

.

A +1

Поскольку второй случай соответствует максимальной потере кинетической энергии нейтрона, то Е2 – минимально возможная энергия нейтрона после рассеяния. Величину α называют макси-

мальной относительной потерей энергии при одном столкновении нейтрона с ядром. Отметим, что эта величина определяется только атомной массой ядра, а возможный диапазон изменения α лежит от единицы в случае бесконечно тяжелого ядра до нуля в случае самого легкого ядра (водород – А = 1).

Таким образом, энергия нейтрона после упругого столкновения с ядром не может быть любой, а лежит внутри интервала от

αE1 до E1 :
αE1 ≤ E2 ≤ E1 или E2 [αE1; E1].	(3.5)

Интервал энергий [αЕ1; Е1] называется ступенькой замедления. Отметим, что в случае замедления на водороде А = 1 и α = 0 , следовательно, нейтрон может потерять всю свою кинетическую энергию в результате одного столкновения с ядром. Для водорода ступенька замедления имеет вид [0; E1].

3.3.Законы упругого рассеяния

Вразд. 3.2 было показано, что нейтрон с энергией E1 после рассеяния будет иметь энергию E′ в диапазоне [αE1; E1], т.е. энергия

нейтрона после рассеяния лежит в пределах ступеньки замедления. Найдем распределение энергии рассеянного нейтрона ( E′) внутри

93

ступеньки замедления. Это распределение описывается функцией p(E1 → E′), которая представляет собой плотность вероятности то-

го, что нейтрон, обладающий до столкновения энергией E1, после столкновения будет иметь энергию E′. Тогда функция p(E1 → E′)dE′ представляет собой вероятность того, что нейтрон,

обладающий до столкновения энергией E1, после столкновения будет иметь энергию в диапазоне [E′; E′+ dE′].

Для того чтобы определить функцию p(E1 → E′), сначала найдем функцию W (ψ) – плотность вероятности рассеяния нейтрона на угол ψ в системе ЦМ. При этом воспользуемся тем, что в рас-

сматриваемом интервале энергий рассеяние изотропно в системе ЦМ. Схема процесса рассеяния нейтрона на угол ψ в системе ЦМ

приведена на рис. 3.6.

dψ

a

R

	b	ψ
O•	r		O
			•
R			r
a1	b1

Рис. 3.6. Схема рассеяния нейтрона в системе ЦМ

На рис. 3.6 точкой О обозначена точка рассеяния. Все нейтроны, направление движения которых после рассеяния ограничено кривыми a-a1 и b-b1, рассеялись в dψ около ψ . Так как рассеяние изо-

тропно в системе ЦМ, то вероятность рассеяния в dψ около ψ

	равна	S*	, где S – площадь сферы; S*	– часть площади сферы, ог-
		S

94

раниченная кривыми a-a1

и b-b1 (заштрихованная область на

рис. 3.6). Площадь сферы S = 4πR2 . Поскольку dψ –

элементар-

ный угловой

диапазон,

то

S* = 2π r

ab

= 2π Rsin ψ Rdψ =

= 2πR2 sin ψdψ , так как r = R sin ψ , а

ab

= Rdψ.

Вероятность

рассеяться

на

угол

dψ

описывается

функцией

W (ψ)dψ . Таким образом,

W

(ψ)dψ =

S*

=

2πR2 sin ψdψ

=

1

sin ψdψ .

4πR2

S

2

Из последнего выражения следует, что

W (ψ)=

1

sin ψ .

(3.6)

2

π

1

π

1

Очевидно, что ∫dψW (ψ)

=

∫dψsin ψ =

2 =1, т.е. вероятность

0

2

0

2

рассеяния на любой угол в интервале от 0 до π равна единице.

Из курса теории вероятности известно, что для двух функций(x) и ( y) в случае, если переменные x и y однозначно связаны

между собой, справедливо следующее выражение:

(x) dx = (y) dy(x) ,

которое представляет собой равенство соответствующих вероятностей.

В рассматриваемом случае известна функция W (ψ), а надо определить функцию p(E1 → E′), в которой переменная E′ однозначно связана с переменной ψ выражением (3.4), т.е. в рассматриваемом случае E′ = E′(ψ). Используя вышеприведенные соотношения, получаем:

95

p(E1

→ E′)

dE'

=W (ψ)

dψ

;

(3.7)

p(E1

→ E′)=W (ψ)

dψ

.

dE′

Первое из приведенных выражений имеет очевидный физический смысл: поскольку энергия нейтрона после рассеяния E′ однозначно связана с углом рассеяния в системе ЦМ ψ выражением (3.4), то вероятность рассеяния в энергетический интервал dE′ равна вероятности рассеяния в соответствующий угловой интервал dψ.

dψ

Найдем dE′ из (3.4):

cos ψ =	(A +1)2		E′	−	A2 +1	.
	2A		E
					2A
		1

После дифференцирования правой и левой частей этого уравнения получим:

−sin ψdψ = (A +1)2 dE′; 2AE1

	dψ		1		(A +1)2	.
		=
	dE′
			sin ψ 2AE1

После подстановки последнего выражения и (3.6) в (3.7) находим, что:

p(E1 → E′)=

1

sin ψ

1

(A +1)2

=

(A +1)2

1

.

2

sin ψ

2AE1

4A

E1

A −1

2

A2 − 2 A +1

Учитывая, что α =

=

, имеем:

(A +1)2

A +1

A −

1

2

A2 + 2 A +1 − A2 + 2 A −1

4 A

.

1 − α = 1 −

=

=

(A +1)2

(A +1)2

A +

1

96

Окончательно получаем выражение для p(E1 → E′):

	p(E1	→ E′)=		1	.	(3.8)
			(1	− α)E1

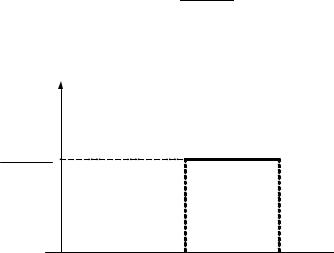
Отметим, что последнее выражение не зависит от E′ – кинетической энергии нейтрона после рассеяния. Зависимость (3.8) представлена на рис. 3.7. Вероятность того, что после рассеяния нейтрона его энергия будет лежать внутри ступеньки замедления, определяется выражением:

Y = αE∫1 dE′p(E1 → E′)= E1(11− α) E1(1− α)=1.

E1

p (E1 →E')

1

E1(1−α)

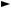E

αE1 E1

Рис. 3.7. Закон упругого рассеяния (распределение нейтронов по энергии после рассеяния внутри ступеньки замедления)

Таким образом, закон упругого рассеяния гласит, что после рассеяния при энергии Е1 нейтроны равномерно (равновероятно) распределены внутри ступеньки замедления.

97

Зная p(E1 → E′), можно рассчитать любые величины, характе-

ризующие акт рассеяния нейтрона на ядре. Рассмотрим некоторые из этих величин.

1. Средняя потеря энергии нейтрона на одно столкновение с ядром массой А, т.е.

∆E = (E1 − E′),

E1

∫dE′p(E1 → E′) (E1 − E′)

			=	αE1				.
∆		E
				E1	′	′	)
				∫dE p(E1		→ E

αE1

Вероятность замедлиться в пределах ступеньки замедления:

E1

∫dE′p(E1 → E′)=1 . Тогда далее получаем:

αE1

E

(E1 − E′)

E1

E1(1−α)

E

= ∫1 dE′

=

− ∫1dE′ E′

1

=

∆

E

(1−α)E1

(1

αE

−α)E1

αE

(1−α)E1

1

1

= E

−

1

1

(E2 −α2E2 )= E −

E1(1−α)(1+ α)

=

= E −

E1(1+α)

.

1

(1

−α)E

2

1

1

1

2(1−α)

1

2

1

Отсюда следует, что средняя энергия после столкновения

E′ = E1 1+2α ; средняя потеря энергии на одно столкновение

∆E = E1 1−2α .

2. Средний косинус угла рассеяния в ЛС. В рассматриваемой об-

ласти энергий рассеяние изотропно в системе ЦМ (т.е. средний косинус угла рассеяния cos ψ = 0 ). Рассчитаем cosΘ – средний коси-

нус угла рассеяния в ЛС.

Прежде всего, найдем связь между cosψ и cosΘ . Из рассмотре-

ния приведенной на рис. 3.4 схемы следуют следующие соотношения:

98

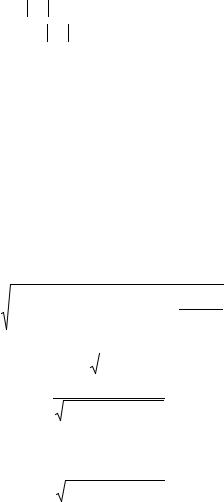
ОА = VЦМ + Va cos ψ,

ОA = V2 cosΘ .

Следовательно,

VЦМ + Va cos ψ = V2cosΘ .

(3.9)

Используя

полученные

выше

выражения для

скоростей

V = V

1

,

V

= V

A

,

V2 = V2

+ V2

+ 2V V

cosψ, по-

ЦМ 1 A +1

a

1 A +1

2

a

ЦМ

a ЦМ

сле подстановки их в (3.9) получим:

V

1

+ V

A

cos ψ =

1 A +1

1 A +1

A

2

V

2

+ 2V2

Acos ψ

= cosΘ

V

+

1

(A +1)2

;

A +1 1

A +1

1

1+ Acos ψ = cos Θ

A2 +1+ 2Acos ψ ;

cos Θ =

1+

Acos ψ

.

(3.10)

1+ A2 + 2Acos ψ

Определим средний косинус угла рассеяния в ЛС, используя полу-

ченную связь (3.9):			f (ψ)=					1+ Acos ψ		= cosΘ . Под средним
								1+ A2 + 2Acos ψ
значением функции			f (ψ)			понимается следующее выражение:
					π
					∫dψ f (ψ)W (ψ)
		f (ψ)=			0				,	(3.11)
						π
						∫dψ W (ψ)
						0
где W (ψ)= 1			π			W (ψ)=1 .
	sin ψ и ∫dψ
2			0

99

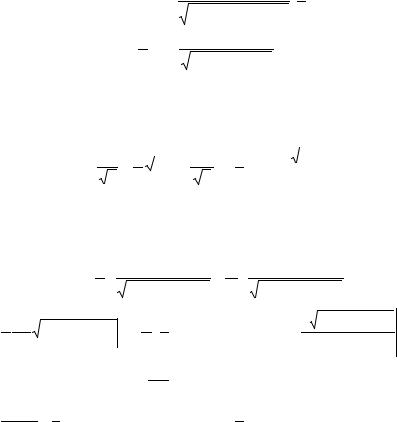
					π	1+ Acos ψ			1 sin ψ =
f (ψ)=		cos Θ	=		∫dψ
					0	1+ A2 + 2Acos ψ			2
=				1	1	1+ A x	,
				2	∫dx	1+ A2 + 2A x
					−1

где x = cos ψ.

Используя справочные данные [2]:

dx

2

xdx

1

2

z

z ,

∫

=

∫

=

z −a

,

z

b

z

3

b

2

где z = a +bx , выполним тождественные преобразования последнего выражения, учитывая, что А > 1:

1

1

dx

A 1

xdx

cos

Θ =

+

=

2

∫

∫

−1

1+ A2 + 2A x

2 −1

1+ A2 + 2A x

=

1 2

2

+2A x

1

A

1

2

2

2 1+ A2 +2A x

1

2 2A

1+ A

+

3

(1+ A

+2A x)−1− A

4A2

=

−1

2

−1

=21A [1+ A − (A −1)]+

+2 A2 1 (1+ A2 +2A)−1− A2 (1+ A)− 1 (1+ A2 −2A)−1− A2 (A−1) = 2 4A 3 3

				1					1					2								2				2					2														2							2						2			2
	=						+											A −					−						A				(1+ A)								−		−				A −									A				−					(A −1)			=
				A												3						3				3																			3							3									3
										4A
	1					1			2							2			2			2			2					2		2					2				3			2			2			2						3 2							2			2	2		2
=			+										A−					−			A		+						A		−				A−					A		+			A			+						A						A−					A−		A −				=
	A				4A											3			2						3							3					3							3						3							3						3			3
									3																																																												3
																						=		1			−				1				4	=		1			−			1			=			2				.
																														4A					3			A					3A
																								A																									3A

100