Крючков Теория переноса нейтронов 2007

Для того чтобы найти F(E), надо решать уравнение замедления последовательно в пределах каждой из ступенек замедления. Сделаем это для первой ступеньки замедления (E [αE0 , E0 ]). Уравнение замедления в пределах первой ступеньки замедления имеет вид

	− FS(1)(E)+ E∫0 d E′	FS(1)(E′)	+ qδ(E − E0 )= 0 ,	(3.41)
		(1− α)E′
	E

где верхний индекс (1) подчеркивает, что ищется плотность рассеяния в пределах первой ступеньки замедления. Будем искать решение уравнения (3.41) в виде

F (1)(E)= (1)(E)+ qδ(E − E	0	),	(3.42)
S

где функция (1) (E) представляет собой плотность столкновений

(рассеяний) рассеянных нейтронов в пределах первой ступеньки замедления; qδ(E − E0 ) – плотность рассеяния нейтронов источни-

ка (плотность первых столкновений); FS (E) – полную плотность

рассеяния нейтронов в пределах первой ступеньки замедления. Подставим выражение (3.42) в уравнение (3.41):

	− (1)(E)−qδ(E − E0 )+ E∫0 d E′		(1)(E′)		+		q		+ qδ(E − E0 )= 0 ;
			(1−α)E′				(1−α)E0
	E
	− (1)(E)+ E∫0 d E′		(1)(E′)	+			q		= 0 .	(3.43)
						(1−α)E0
	E	(1−α)E′

Последнее слагаемое в уравнении (3.43) описывает источник нейтронов, сформированный однократно рассеянными при энергии E0 нейтронами. Продифференцируем уравнение (3.43) по Е, ис-

пользуя правило дифференцирования интегральной функции, где переменная дифференцирования стоит в качестве нижнего предела интегрирования:

121

−d (1)(E)− (1)(E)d E = 0 ,

(1−α)E

что приводит к дифференциальному уравнению

d (1)(E)	= −	d E
			.
(1)(E)		(1− α)E

Решением последнего дифференциального уравнения является функция

(1)(E)=		C			.		(3.44)
		1
		E	1−α
Константу С найдем, сравнивая выражения							(3.44) и (3.43) при
Е = Е0. Уравнение (3.43) при Е = Е0 переходит в равенство:
(1) (E0 ) =		q				,
	(1− α)E0

а из (3.44) следует, что (1) (E0 ) = C1 . Сравнивая два последних

E01−α

равенства, приходим к следующему выражению:

C				q
			=		.
	1			(1−α)E0
E01−α

Отсюда имеем, что

C= 1−qα E01−αα ,

иокончательно для плотности столкновения рассеянных нейтронов получаем

122

		q		α
			E01−α
(1)(E)=	1−α					,	(3.45)
			1

E1−α

а для полной плотности рассеяния в пределах первой ступеньки замедления:

	q		α
		E01−α						E [αE		].
F (1)(E)=	1−α				+ qδ(E − E	0	),		, E		(3.46)
		1
S								0	0

E1−α

Запишем решение (3.45) в переменных летаргии, учитывая, что

(1)(u)= (1)(E) E и E = E0 e−u :

q

α

1

q

α

α

F (1)(u)=

E1−

=

E

−

=

E01−α

1−α

E01−α

1−α

1

−α

1

− α

α

α

α

α

q

E0−

eu

q

eu

=

E01−α

1−α

1−α

=

1−α

.

1

− α

1

− α

Таким образом, плотность столкновений рассеянных нейтронов в пределах первой ступеньки замедления в переменных летаргии имеет вид

	(1)(u)=			q	eu	α
						1−α	(3.47)
		1		−α

и зависит от летаргии в отличие от случая замедления на водороде. Рассмотрим теперь уравнение замедления в пределах второй

ступеньки замедления (E [α2 E0 , E0 ]):

		E		FS (E′)
	− FS(2)(E)+ α∫d E′				= 0 ,	(3.48)
				(1− α)E′
		E

123

где FS(2) – плотность рассеяния, определенная во второй ступеньке

	′	равна или известной функции						(1)	′
	замедления, а FS (E )								(E ) в пре-
					E
	делах первой ступеньки замедления		E [αE0	,		]	, или искомой
					α

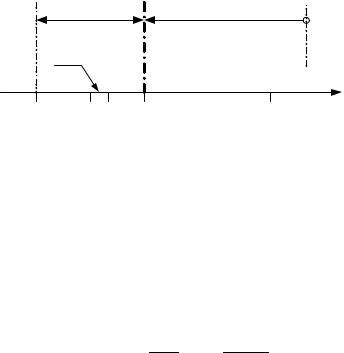
функции FS(2) (E′) в пределах второй ступеньки замедления (E [E, αE0 ]) – рис. 3.14. В уравнении (3.48) разобьем интеграл на два интеграла, соответствующие каждой из ступенек замедления:

αE

FS

(2)

(E′)

E

(1)

(E′)

FS(2)(E)=

1

0 d E′

+

1

α∫ d E′

. (3.49)

∫

E′

1

−α

E′

E

1− α αE0

F2(E)	1(E)
dE
	E
	0	E

α2E	E αE	E / α
0	0

Рис. 3.14. Схема для расчета плотности рассеяния во второй ступеньке замедления

Так как (1)(E′)	определена равенством (3.45), то интегральное
уравнение (3.49)	может			быть решено относительно функции
F (2)(E). Покажем, что				плотность рассеяния имеет разрыв при
S
E = αE0 , т.е. на границе первой ступеньки замедления. Для этого из
(3.49) найдем F (2)(αE		0	):
S

FS(2)(αE0 )= 1−1α E∫0 d E′ (1E)(′E′) .

αE0

124

В то же время из (3.43) следует:

			1	E			(1)	(E′)		q
FS(1)(αE0 ) =				∫0	d E′				+		.
	1						E′			(1−α)E0
			−α αE0

Сравнивая два последних уравнения, можно сделать вывод, что плотность рассеяния имеет разрыв на границе первой ступеньки

q

замедления, и величина этого разрыва равна (1− α)E0 . После ре-

шения уравнения замедления в пределах второй ступеньки замедления можно решить его в третьей ступеньке и т.д.

Рассмотрим асимптотическую область энергий. Считается, что асимптотическая область энергий начинается после третьей ступеньки замедления от энергии источника. Нейтрон должен испытать достаточно много столкновений с ядрами среды для того, чтобы его энергия попала в асимптотическую область. Асимптотическая область энергий характеризуется тем, что плотность рассеяния Fас(E) уже не зависит от номера ступеньки замедления. Уравнение

замедления в асимптотической области энергий имеет вид

				E				d E′
	Fас(E)= α∫Fас(E′)								,
								′
	а его решение:			E				E (1−α)
				C
	F	(E)=				,	C = const .
	ас			E

Найдем константу С, воспользовавшись тем, что в бесконечной однородной непоглощающей среде j(E)= const = q . Определим плотность замедления в асимптотической области энергий:

E

(E − αE′)d E′

C

E

E − αE′

j(E)=

α∫

F(E′)

=

α∫

d E′

=

(1− α)E′

2

E

1− α E

E′

125

E

E

E

C

1

Cα α d E′

C

Cα

[1 − α]−

′

α

=

E

−

E∫

=

lnE

=

1−

α

E′

E

1− α

E′

1− α

1− α

E

α

= C −C

α

ln

E

− lnE

= C

1−

α

ln

1

= C

1+

α

lnα

= q .

1−

α

1− α

α

1− α α

Вспомним, что согласно (3.14):

ξ =1+ 1−αα lnα.

Таким образом, окончательно получаем C = qξ , и для асимптотиче-

ской плотности рассеяния:

	F	(E)=		q			(3.50)
	ас			ξE
	или для асимптотического спектра нейтронов:
	Φас(E)=			q		.	(3.51)
			ξΣS (E)E

В переменных летаргии выражения (3.50) и (3.51) можно переписать следующим образом:

	F	(u)=		q	,		(3.52)
	ас			ξ
	Φас(u)=			q		.	(3.53)
			ξΣS (u)

Отметим, что в асимптотической области энергий устанавливается спектр Ферми – выражения (3.50) – (3.53). Показано, что использо-

126

вание Φас(E) в виде спектра Ферми оправдано уже для четвертой ступеньки при замедлении даже на легких ядрах.

На рис. 3.15 приведен график функцииFS (u) в относительных

единицах для разных атомных масс замедлителя А. Впервые эта функция была получена и исследована чешским ученым Плачеком в 1948 г., поэтому она носит название «функция Плачека».

Видно, что в пределах первой ступеньки замедления поведение функции плотности рассеяния нейтронов определяется выражением (3.47), на границе первой ступеньки замедления исследуемая функция терпит разрыв, а после третьей ступеньки замедления выходит на асимптотическое значение (3.50).

	1 − α	F (u) 2,8
	q	S
		2,6
		2,4
		2,2
		2,0
		1,8
		1,6
		1,4
		1,2
		1,0

u

ln(1/ α)

Рис. 3.15. Функция Плачека для разных масс ядер замедлителя

127

3.9. Замедление в непоглощающей среде, состоящей из смеси нуклидов (асимптотическая область энергии)

Рассмотрим бесконечную неразмножающую гомогенную и непоглощающую (Σa = 0) среду с равномерно распределенным объемным монохроматическим источником нейтронов мощностью q , испускающим нейтроны с энергией E0 . Для этого приведем уравнение замедления в асимптотической области энергий:

		E		FS (E′)
	− FS (E)+ α∫d E′				= 0 .
				(1− α)E′
		E

Это уравнение записано для случая, если среда состоит из одного нуклида. Если среда состоит из смеси нуклидов, то необходимо учитывать замедление на каждом из них, и уравнение замедления записывается в виде суммы соответствующих уравнений для каждого из нуклидов:

E

ii (E)Φас(E)+ ∑i 1−1α α∫i d E′ ΣSi (E′E)Φ′ ас(E′) = 0 . (3.54)

iE

Вуравнении (3.53) Φас(E) – асимптотический спектр. Отметим,

что асимптотический спектр нейтронов устанавливается в среде и не зависит от типа нуклида i , на котором происходит рассеяние нейтрона. В то же время сечения рассеяния и максимальная относительная потеря энергии на одно столкновение зависят от типа нуклида. Предположим, что макроскопические сечения рассеяния для разных нуклидов зависят от энергии единым образом, т.е. выполняется равенство:

ΣSi (E )= ΣSi f (E ).

(3.55)

128

Отметим, что на практике сечения рассеяния для замедлителей в рассматриваемой области энергий вообще не зависят от энергии, т.е. f (E)=1 . Используя (3.55), перепишем уравнение (3.54) сле-

дующим образом:

E

			ΣSi		α		f (E′)Φас(E′)
	− Φас(E)f (E)∑ΣSi	+ ∑			∫i	d E′		= 0 .	(3.56)
			1− αi				E′
	i	i			E
	Введем обозначения: ΣS ≡ ∑ΣSi				– полное макроскопическое сече-
			i

ние среды; Fас(E)= Φас(E)f (E)ΣS – асимптотическая плотность рассеяния. В этом случае уравнение (3.56) принимает вид

				ΣSi		E		Fас(E′)
		1				α
	Fас(E)= ∑					∫i	d E′		.
	i	1− αi ΣS E						E′

Решением этого уравнения является функция

F (E)=

C

.

(3.57)

ас E

Действительно, подстановка (3.57) в уравнение приводит к тождеству:

ΣS

E

C

1

i

αi

C

= ∑

∫ d E′

=

E

1

E′

2

i

− αi ΣS E

= ∑

1

ΣS

1

α

C

∑ΣS

i

C

i

i

C

−

i

=

=

.

1− αi

ΣS

E

ΣS

E

i

E

E

Так как рассматривается непоглощающая среда, то константу С определим из условия того, что плотность замедления – величина постоянная и равна мощности внешнего источника. Если среда состояла из одного нуклида, то уравнение для плотности замедления имеет вид

129

E

j(E)= α∫d E′ FS (E′) E −αE′ .
E	(1−α)E′

Если среда состоит из смеси нуклидов, то уравнение для плотности замедления будет представлять собой сумму уравнений для каждого из них:

E

d E′ΣSi Φас(E′)(E −αi E′) =

j(E)= ∑ ∫i

α

i

E

(1−αi )E′

= ∑ΣSi

E

d E′ΣS f (E′)Φас(E′)(E −αi E′) =

∫i

α

(1−αi )E′

i ΣS E

ΣSi

E

d E′ Fас(E −αi E′)

= ∑ΣSi C

E

d E′(E −αi E′) =

= ∑

∫i

∫i

α

α

i ΣS E

(1−αi )E′

i ΣS

E

(1−αi )E′

= ∑

ΣSi

E

1

αi

αi

E

C

−

−

ln

=

ΣS

E

1

−αi

i

1− αi

E

αi E

= ∑

ΣS

i

α

i

= C∑

ΣS

i

C 1+

ln α

i

ξ

.

i ΣS

1−αi

i

i ΣS

Таким образом, если определить среднелогарифмическую потерю энергии в среде, состоящей из смеси нуклидов, следующим образом:

		= ∑	ΣSi	ξi ,	(3.58)
	ξ
		i	ΣS

то для плотности замедления в асимптотической области энергии

	получим выражение j(E)= q = C		, а следовательно, C =		q			и
		ξ
					ξ
	асимптотическая плотность рассеяния определяется выражением

130