Крючков Теория переноса нейтронов 2007

∆j(rr, τ)− ∂j(r , τ) = 0;

∂τj(rr,0) = S(rr).

Для получения решения в среде с поглощением необходимо, согласно (4.8), найденное решение умножить на вероятность избежать поглощения при замедлении от τ = 0 до текущего значения τ. Отметим, что вероятность избежать поглощения при замедлении может быть рассчитана любым из известных способов, рассмотренных в гл. 3, независимо от решения уравнения возраста.

4.4. Возраст нейтронов и время замедления

Возраст нейтронов τ зависит от Е – текущего значения энергии, и Е0 – энергии источника:

u	du	E
τ = ∫		= ∫0	1		dE′	≡ τ(E0 , E).	(4.9)
	3ξΣtr ΣS
0		0 3ξΣtr ΣS E′

Отметим, что возраст нейтронов, энергия которых равна энергии источника Е0, равен нулю. В процессе замедления возраст нейтронов, как и летаргия, возрастает. Поскольку макроскопические сечения измеряются в см–1, то единица измерения возраста – см2. В дальнейшем будет показано, что τ определяет средний квадрат смещения нейтрона при замедлении от Е0 до Е.

Происхождение названия «возраст нейтрона» связано с тем, что τ однозначно связан и с хронологическим возрастом нейтронов – средним временем замедления нейтрона от Е0 до Е. Действительно, если V – скорость нейтрона, то dS = Vdt – путь, проходимый ней-

троном за время dt, а Vdt (где λS – средняя длина свободного

λS

пробега до рассеяния) – среднее число актов рассеяния на ядрах среды, которое испытал нейтрон на пути dS. В среднем за одно рас-

171

сеяние летаргия возрастает на ξ , т.е. после

Vdt

рассеяний прирост

λS

летаргии

du

можно определить как

du =

Vdt

ξ .

Поскольку

λS

dτ =

du

,

то после подстановки выражения

для

du

имеем:

3ξΣS Σtr

dτ =

Vdtξ

= DVdt . Отсюда легко получить

среднее

время

λS 3ξΣS Σtr

замедления до возраста τ :

τ

dτ'

T (τ)= ∫

.

(4.10)

D(τ')V(τ')

0

Получим T(E0 , E) – среднее время замедления нейтрона от E0 до E. Для этого надо перейти от переменной «возраст» к переменной «энергия» в последнем выражении, воспользовавшись равенством:

dτ = D(u)du = − D(E)dE .

ξΣS (u) ξΣS (E)E

С учетом этого равенства и того факта, что возраст, равный нулю, соответствует Е0, получим искомое выражение:

T (E0 , E) = E∫0	1		dE′	.	(4.11)
E V(E)ξΣS (E) E′

Получим формулу для определения времени замедления нейтронов. Для этого в уравнении (4.11) перейдем от энергии к скоро-

сти, воспользовавшись равенством E = 12 V2 , dE = VdV , поскольку

масса нейтрона равна одной атомной единицы массы, и получим выражение для времени замедления через скорость нейтронов:

172

T (V0 , V)= 2V∫0 ξΣdV′′2 ,

V S V

где V0 – скорости нейтронов источника; V – текущее значение скорости.

Поскольку в области замедления сечение рассеяния слабо меняется от энергии нейтрона: ξΣS = ξΣS , то время замедления можно

0

2

1

рассчитать по формуле:

T (V , V)=

1

−

. Практически

ξΣS V

V0

всегда V >> V , поэтому

1

<<

1

и

время

замедления можно

0

V0

V

оценить по формуле: T

2

. В табл. 4.1

приведены характер-

ξΣS V

ные времена замедления и возраст нейтронов для разных замедлителей при замедлении от 2 МэВ до 1 эВ (границы тепловой области энергий).

				Таблица 4.1
Характерные время замедления и возраст нейтронов
		для основных замедлителей
Замедлитель			Тх106, с	τ , см2
H2	O		6,7	27
D2	O		48	120
Be			59	98
C			149	350

Отметим, что все полученные выше формулы носят приближенный характер, поскольку еще до первого столкновения нейтрона с ядром он прошел некоторый путь от источника, на протяжении которого его возраст не менялся и был равен нулю, и который ни одна из приведенных выше формул не учитывает. А, с другой стороны, после последнего столкновения с ядром, когда у нейтрона энергия станет равной Е, нейтрон пройдет некоторый путь в среде до столкновения с ядром, а следовательно, до изменения своей

173

энергии. Этот факт также не учтен ни в одной из формул. Все это следствие того факта, что приведенные выше формулы получены в рамках модели непрерывного замедления, хотя реально замедление носит ступенчатый характер. Для учета перечисленных выше эффектов, например при сравнении экспериментальных и расчетных данные, в формулу для возраста (4.9) необходимо прибавить член, учитывающий пробег до первого и после последнего столкновения нейтрона с ядром:

	τ(u) = {2λ2S (0) + 2λ2S (u)}+ u∫du′	D(u′)	.
		ξΣS (u′)
	0

Поправочный член в фигурных скобках может быть очень существенным. Так, для воды он составляет примерно одну треть полного возраста при замедлении от энергии деления до границы тепловой области энергий. Особенно существенным этот член становится при описании замедления быстрых нейтронов, что будет рассмотрено в разд. 4.8.

Формула (4.9) не учитывает также отклонение от моноэнергетичности источника нейтронов. Если источник нейтронов имеет спектр χ(E) (например, спектр деления), то вместо формул (4.9) и

(4.11) необходимо использовать следующие формулы:

τ(E)= ∞∫dE′χ(E′)τ(E′, E)

0

и

T (E)= ∞∫dE′χ(E′)T (E′, E).

0

При этом для спектра деления в средах, состоящих из смеси замедлителя и тяжелых ядер, становится необходимо учитывать процессы неупругого рассеяния нейтронов на тяжелых ядрах. Этот эффект будет обсуждаться в разд. 4.8.

174

4.5. Условия однозначного выбора решения уравнения возраста в физических задачах

Уравнение возраста ∆j(rr, τ)−	∂j(rr, τ)	= 0 представляет собой
	∂τ

дифференциальное уравнение второго порядка и имеет в общем решении две неопределенные константы, т.е. с математической точки зрения оно имеет бесконечное множество решений. Но для физически однозначно сформулированной задачи необходимо из всего бесконечного множества решений выбрать одно, соответствующее именно рассматриваемой постановке физической задаче. Это достигается путем использования одного или нескольких условий, приведенных ниже.

1. Условие неотрицательности и ограниченности плотности замедления. Исходя из определения для плотности замедления, должно выполняться следующее условие:

0≤ j(r, τ) ≤ S(r ) .

2.Условие на внешней невогнутой границе среды с вакуу-

мом. Это условие получается из соответствующего условия для плотности потока в диффузионном приближении:

Φ(rS + αn , τ )= 0 ,

где rrS – радиус-вектор границы; α = 0,71 λtr – длина линейной

экстраполяции потока в вакуум, путем использования выражения для связи плотности потока и плотности замедления:

j(r , τ)= ξΣS (τ)Φ(r , τ) .

Тогда условие для плотности замедления имеет вид:

j(rS + αn, τ)= 0 .

175

Отметим, что α через величину λtr зависит от τ , так как при разных энергиях Σtr различно. Но поскольку рассматриваются боль-

шие среды, и размеры среды велики по сравнению с λtr ,				то можно
~	~	не зависит от	τ , и тогда для всех значе-
считать, что α	= 0,71 λtr
ний возраста	можно	использовать	одно граничное	условие

j(rS + α~ n, τ)= 0. Более того при реальных расчетах больших сред

часто пренебрегают экстраполированной добавкой и используют условие равенства плотности замедления нулю на реальной границе «среда – вакуум». При этом сознательно идут на ухудшение и так «плохого» решения уравнения возраста в области около границы «среда – вакуум», анализируя решение уравнение возраста внутри рассматриваемой области (далеко от границы «среда – вакуум)».

3. Условия на границе раздела сред с разными свойствами.

Эти условия получаются из соответствующих условий для плотности потока нейтронов в диффузионном приближении на границе раздела двух сред:

Φ		(r	, τ) = Φ		2	(r	, τ);
	1	S				S
				r		, τ)	= D	(τ)	Φ		r
D (τ) Φ				(r						2	(r , τ)
	1		n 1	S			2	n			S

путем использования выражения для связи плотности потока и

плотности замедления Φ(rr, τ)= j(rr, τ) . Подставив это выражение

ξΣS (τ)

в приведенную выше систему, получим условия для плотности замедления:

j

(rr

, τ)

j

2

(rr

, τ)

1

S

=

S

;

(ξΣ

S

(τ))

(ξΣ

S

(τ))

1

2

D(τ)

r

D(τ)

r

n j1(rS

, τ)

=

n j2 (rS , τ).

ξΣS

(τ)

ξΣS (τ)

2

1

176

Таким образом, если плотность потока на границе раздела двух сред непрерывна, то плотность замедления терпит разрыв, величина которого равна отношению замедляющих способностей сред (ξΣS ). Точно так же, как и при анализе диффузионного приближе-

ния, надо понимать, что уравнение возраста дает максимальную погрешность около границы раздела двух сред с разными свойствами, и анализировать его решение имеет смысл только на расстояниях более трех длин свободного пробега нейтрона от рассматриваемой границы.

4. Условие внешнего источника. Это так называемое началь-

ное условие, или условие при τ = 0:

j(r ,0)= S(r ),

где S(r ) – заданная мощность источника нейтронов с τ = 0

τ = 0 (u = 0, E = E0 ).

4.6. Решение уравнения возраста

Рассмотрим несколько характерных задач, которые решаются с использованием возрастной теории.

Задача 1. Определить плотность замедления от плоского моноэнергетического источника мощностью S [1/(cм2с)], расположенного в центре бесконечной гомогенной пластины толщиной а, кото-

рая окружена вакуумом (рис. 4.2).
Уравнение возраста для			τ > 0	(вне энергии источника) имеет
вид
		∂2 j(x, τ)		=	∂j(x, τ)		.
			∂x2		∂τ
Источник	расположен		в пространстве при х = 0, т.е.
S(x)= Sδ(x),	а соответствующее начальное условие по возрасту

177

имеет вид j(x, 0)= Sδ(x). Будем считать границы пластины (± а/2)

экстраполированными, тогда граничные условия нашей задачи имеют вид j(± a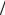2,τ)= 0 для любого возраста, большего нуля.

Очевидно, что задача – симметричная относительно х = 0, т.е. имеет место условие симметрии: j(− x, τ)= j(x, τ).

S(E00))

С Р Е Д А

Вакуум

Вакуум

xХ

–-aa/2

0

aa/2/2

Рис. 4.2. Плоский источник в центре пластины

Уравнение возраста решается методом разделения переменных, т.е. решение ищется в следующем виде:

j(x, τ)= ∑ fn (τ)ψn (x) .	(4.12)
n

В этом случае граничные условия и условие симметрии примут вид

ψn (±a / 2) = 0 – граничные условия,	(4.13)
ψn (−x) = ψn (x) – условие симметрии.	(4.14)

После подстановки (4.12) в исходное уравнение получим:

	d 2ψn (x)			dfn (τ)
∑ fn (τ)			− ψn (x)			= 0 .
	dx	2		dτ
n

178

Разделим обе части уравнения на fn (τ)ψn (x) :

ψ′n′(x)			−	fn′(τ)		= 0 .
∑
	ψn (x)
n				fn (τ)

В последнем уравнении первое слагаемое зависит только от переменной x, а второе – только от переменной τ. Эти переменные независимы, а значение выражения в квадратных скобках при любых значениях каждой из переменных всегда равна нулю. Это возможно только в случае, если первое и второе слагаемые равны одной и той же константе. Рассмотрим возможные варианты: положительная и отрицательная константы (константа, равная нулю не рассматривается, поскольку соответствует тривиальному решению).

Если константа положительная: Bn2 > 0 , то для функции ψn (x)

получается уравнение: ψ′n′(x) = Bn2ψn (x) , общее решение которого

имеет вид ψn (x) = C1 exp(Bn x) + C2 exp(−Bn x) и не может удовлетворить граничным условиям (4.13), кроме тривиального решения при С1 = С2 = 0.

Если константа отрицательная: − Bn2 < 0 , то для функции ψn (x)

получается следующее уравнение с соответствующим граничным условием:

			2	ψn (x)
		d			= −B2ψ			n	(x);
			dx2			n
							(a		2)= 0 .
	ψ		n	(− a 2)= ψ		n
Общее	решение			этого			уравнения			имеет	вид
ψn (x) = Cn	cos(Bn x) + Cn			sin(Bn x) .
1	2

Чтобы удовлетворить условию симметрии (4.14), необходимо положить константу Cn2 = 0, поскольку синус – функция нечетная

и не удовлетворяет (4.14).

179

Таким образом, ψn (x) = Cn cos(Bn x) . Для определения константы Вn воспользуемся граничным условием (4.13):

	a			a
Cn cos Bn			= Cn cos − Bn		= 0 .
	2			2

Отсюда следует, что Bn a2 = π2 + πn, n = 0,1, 2, ... . Получаем вы-

ражение для определения константы Вn:

	B = π		(1+ 2n),				n = 0,1, 2, ... .	(4.15)
	n	a
	Система функций {cos(Bn x)}, где Вn определяются выражением
				a		a
	(4.15), ортогональна на отрезке		−		,		, т.е. выполняется выраже-
				2		2

ние:

a

x)cos(B x)dx = a 2,

n = m;

2

cos(B

(4.16)

∫

m

n

n ≠ m.

a

0,

−2

В рассматриваемом случае (константа отрицательная:

− B2 < 0 )

n

для функции

fn (τ)

получается

следующее

уравнение:

f

n

(τ)B2

+

dfn (τ)

= 0 ,

решением

которого являются

функции:

n

dτ

fn (τ)= An exp(− Bn2τ).

Таким образом, общее решение исходного уравнения возраста, согласно (4.12), имеет вид

j(x, τ)= ∑ n exp(− Bn2τ)cos Bn x ,	(4.17)
n

180