5. Оценки гармонически сопряжённых функций в -пространствах при

Знаменитая теорема М. Рисса утверждает, что если и– взаимно сопряжённые гармонические функции, причём, то присправедлива оценка, где

зависит только от , причём, еслиили.

В этом параграфе нас интересует аналог оценки М. Рисса в -пространствах.

Ясно, что при из теоремы М. Рисса непосредственно следует. Однако хорошо известно, что, несмотря на это, присоответствующая оценка неверна.

Мы докажем, что оператор гармонического сопряжения является ограниченным впри всех.

Лемма 2. Пусть – гармоническая функция в некотором кругеи. Тогда при всехсправедлива оценка

, (18)

где зависит только от.

Доказательство. Если , то оценка непосредственно следует из теоремы о среднем и неравенства Гёльдера. Остаётся доказать лемму при. Не ограничивая общности, можно предположить, что, а. Как и прежде, обозначим черезинтегральные средние от функции, то есть

Не ограничивая общности, будем предполагать также, что

.

В этих предположениях, если при некотором , то лемма будет следовать из принципа максимума, при этом .

Поэтому будем предполагать, что при всех. Поскольку, то

Записывая представление Пуассона для функции по окружности, получаем:

то есть

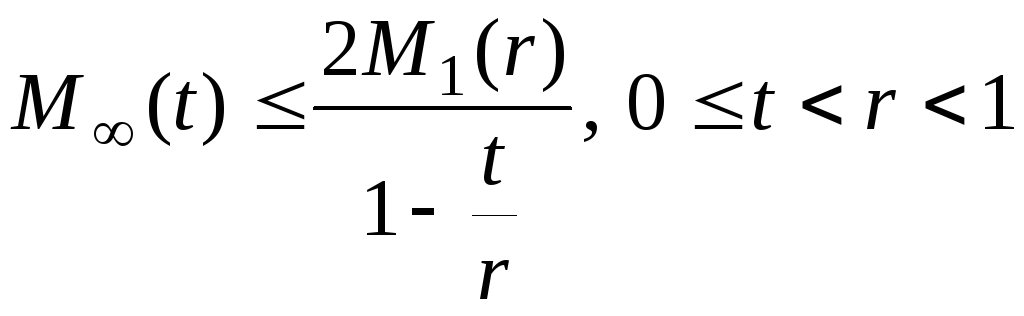. (19)

Пусть теперь – произвольное число, такое, что. Тогда из оценки (19) непосредственно имеем:

.(2.20)

Первый интеграл, очевидно, сходится и равен некоторой константе . Оценим второй интеграл в (20). Ясно, что

.

Следовательно, из неравенства (19) получаем:

. (21)

Поскольку по предположению,, то

.

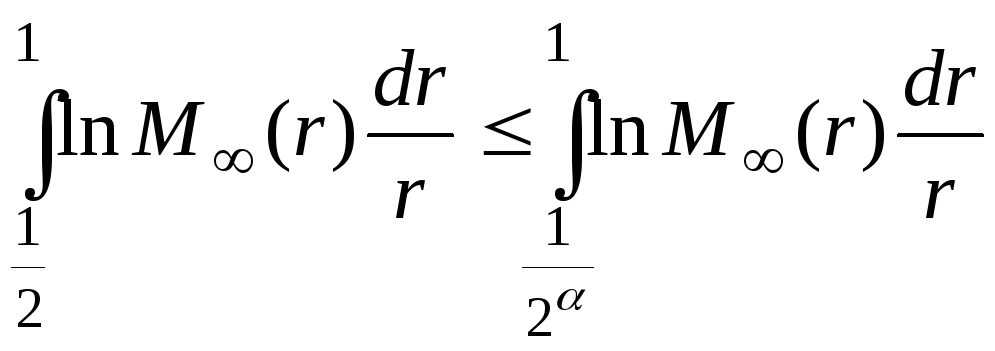Но заменив , последний интеграл можно записать в виде

.

Следовательно, неравенство (21) преобразуется в

.

Теперь подбирая параметр таким образом, чтобы, из последней оценки получаем:

,

то есть

.

Тогда неравенство (18) следует из принципа максимума. Что и требовалось доказать. □

Лемма 3. Пусть – гармоническая функция втакая, что

,

то есть ,. Тогда

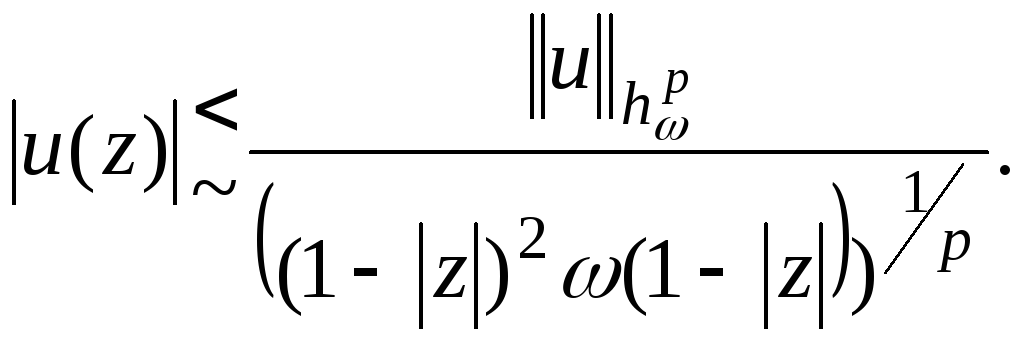
Доказательство. Пусть ,. Применяя лемму 2 к функциипо кругу, получим:

,

Остается положить и повторить рассуждения, проведенные при доказательстве теоремы 1. □

Лемма 4. Пусть ,,– гармонически сопряженная функция с,. Тогда при всех, где, справедлива оценка

(22)

Доказательство. Пусть . Тогда имеем

Поэтому

, (23)

где, как и прежде,

Теперь используя лемму 3, из оценки (23) получим:

Положим , тогда,, и поэтому

Чтобы получить оценку (2.22), достаточно применить следствие 1.1, согласно которому при всех ,. То есть

Напомним, что . Из последнего неравенства немедленно следует утверждение леммы. □

В дальнейшем существенную роль сыграет следующее диадическое разбиение единичного круга . Пусть, где– множество неотрицательных целых чисел,

, ,

.

При этих же , положим– криволинейный прямоугольник с центром, совпадающим с центром, и расширенный 4/3 раза.

Ясно, что система диадических прямоугольников покрывает единичный круг однократно, причем ипересекаются только, возможно, границами, если. Системапокрывает конечнократно.

Справедливо следующее утверждение:

Теорема 10. Пусть . Тогда справедлива оценка

.

Доказательство. Сначала установим оценку

(24)

Пусть – произвольная точка из,,. Тогда из леммы 2.3 имеем:

или

.

Положив и заметив, что при всех

,

по теореме 2.1 будем иметь:

,

откуда приходим к оценке

.

Учитывая последнее неравенство, в итоге получаем:

. (25)

В неравенстве (25) мы учитывали, что для произвольного. Суммируя неравенства (25) пои, выводим:

, ,.

Здесь мы учли, что последовательность покрываетконечнократно. □

Теорема 11. Пусть ,,,– гармонически сопряженная функция с. Тогда

а) , и если, то

, .

б) Если ,, то линейный интегральный оператор

,

при всех отображаетна. При этом

,.

Доказательство. Сначала заметим, что если , где– оператор гармонического сопряжения, то по лемме 2.4при, гдесовпадает спри,. Этому же классу принадлежит функция. Поэтому функцияпринадлежит классу.

Следовательно, доказательство теоремы сводится к установлению пункта б). Учитывая теорему 4 и формулу (7), получаем:

Не ограничивая общности, можно предположить, что , поскольку очевидно, что,,.

Далее заметим, что утверждение б) при непосредственно следует из теоремы 8. Поэтому в дальнейшем будем предполагать, что. Ясно, что

.

Следовательно, учитывая, что , получаем:

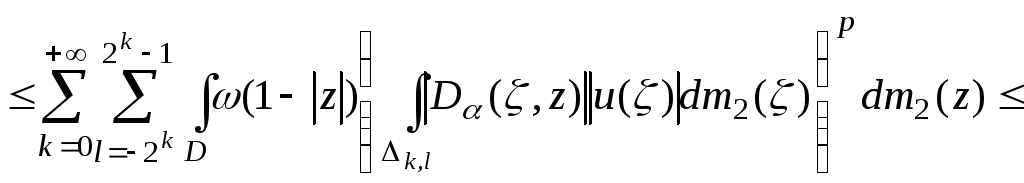
, (2.26)

где – центр прямоугольника,.

Теперь оценим последний интеграл . Используем лемму 1, согласно которой

,

если , то есть.

Следовательно, из (26) получаем:

. (27)

Теперь заметим, что согласно неравенствам (3)

, ,

для произвольного ,,.

Учитывая неравенство (27), окончательно имеем:

.

По теореме 10 последняя сумма не превосходит . □

Из этой теоремы непосредственно следует

Теорема 12. Пусть ,. Тогда следующие утверждения равносильны:

а) ;

б) допускает представление

, ,

где ,– комплекснозначная борелевская мера, для которой

.

Доказательство. Вначале докажем импликацию а)б). Если, то согласно теореме 6допускает представление (11), где.

Согласно теореме 10 мера удовлетворяет условию (24). Чтобы установить импликацию б)а) достаточно повторить вторую часть доказательства теоремы 11. □

Аналог теоремы 12 для случая непосредственно следует из теоремы 8, а именно:

Теорема 13. Пусть ,,. Тогда следующие утверждения равносильны:

а) ;

б) допускает интегральное представление, где.

Лекция №8

ГАРМОНИЧЕСКИ СОПРЯЖЕННАЯ ФУНКЦИЯ

Пусть дана функция U(z), гармоническая в {|r| < 1}, для которой имеет место одно из рассматриваемых представлений. Мы приступаем к исследованию граничного поточечного пове­дения функции, гармонически сопряжённой с U. Функция V(z) называется гармонически сопряжённой с U(z), если U(z)+iV(z)— аналитическая функция в {|r|<1}. Сопряжённые функции определены с точностью до прибавления константы; работая в единичном круге, обычно требуют, чтобы V(0)=0; полученная таким образом гармонически сопряжённая с U(z) функция V(z) обозначается через Ũ(z). Обозначение гармонически сопряжённой функции с помощью волны („тильды") общепринято.