
- •Представление в виде степенного ряда
- •Формула Пуассона
- •Представление Пуассона для гармонических функций Представление Пуассона для гармонических функций, принадлежащих некоторым классам
- •1 Свойства суммируемости гармонических функций, заданных формулой Пуассона
- •2° Первоначальное изучение граничного поведения
- •Формула Коши
- •Формула Коши-Грина
- •Лекция № 4,5,7 -весовое пространство аналитических в круге функций
- •2. Интегральное представление классов
- •3. Интегральное представление гармонических функций
- •4. Ограниченные проекторы в пространствах ипри
- •5. Оценки гармонически сопряжённых функций в -пространствах при
- •Формула для гармонически спряженной функции
- •Интегральное представление классов
- •Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке
- •2 Граничные значения почти всюду равны по модулю единице
- •2 Семестр
- •Приложения неравенства Фейера-Рисса в комплексном анализе. Изучение свойств конформно отображающих функций. Области, ограниченные спрямляемой жордановои кривой
- •1° Производная конформного отображения принадлежит классу н1
- •3 Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы
Приложения неравенства Фейера-Рисса в комплексном анализе. Изучение свойств конформно отображающих функций. Области, ограниченные спрямляемой жордановои кривой
Рассмотрим теперь область , G ограниченную спрямляемой жордановой кривой.
Пусть
Ф— конформное отображение единичного
круга на G
—
область, ограниченную жордановой
спрямляемой кривой Г
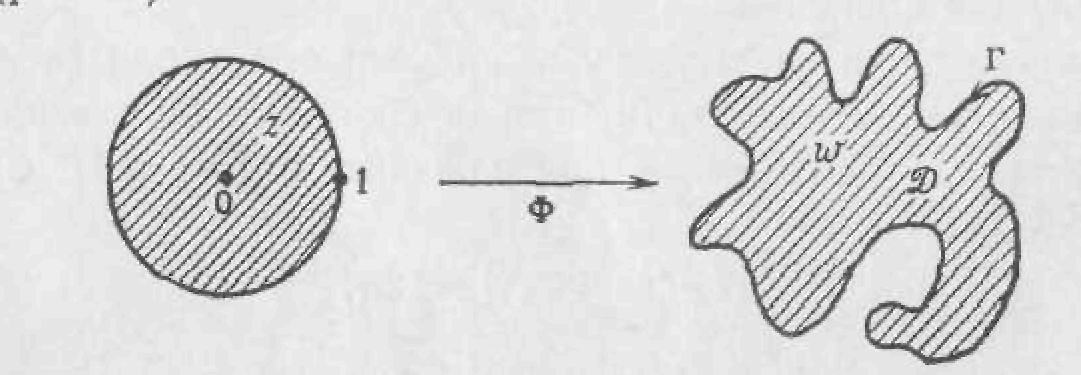
По теореме Каратеодори Ф обладает непрерывным взаимно-однозначным продолжением вплоть до {|r|= 1} и отображает эту окружность на Г. Поэтому ясно, что если [eiθ0, eiθ1,,…, eiθp] — разбиение окружности {| r | = 1}, то [Ф(eiθ0), Ф(eiθ1,),…, Ф(eiθp)] — разбиение кривой Г.
1° Производная конформного отображения принадлежит классу н1
Теорема
![]() .
.
Доказательство
Пусть ε= e2πi/n. Тогда функция
![]()
является субгармонической в {|r|<1}; она непрерывна для |z|<1 в силу непрерывности Ф(z). Поэтому, по принципу максимума, при |z|<1
![]()
Нo если |ζ|= 1 то точки
[Ф(ζ), Ф(εп ζ ),…, Ф(εпζ)]
образуют разбиение кривой Г; следовательно, по определению длины кривой
S(ζ)≤длина Г. Теперь зафиксируем r<1. Мы имеем
Итак, если |z|<1, то S(z)<длина Г. Теперь зафиксируем r< 1. Мы имеем
![]() длины
Г< ∞.
длины
Г< ∞.
Устремляя n к бесконечности и используя непрерывность функции Ф'(rе'е) по θ для r< 1, получаем в пределе
![]() длины Г
длины Г
поскольку
это выполняется для всех r<.1,
то
![]()
Образы множеств меры нуль на единичной окружности
Если А — дуга кривой Г, то Ф взаимно-однозначно отображает некоторую дугу j окружности {|z|=1} на Ʌ. Само определение длины дуги теперь нам дает
![]()
Теорема
(Ф. и М.. Риссы). Если. j
—
дуга единичной окружности и ![]() =
Ф(j),то
=
Ф(j),то
![]()
Доказательство.
По
теореме предыдущего подпункта
![]() ,
поэтому
,
поэтому
![]() при r→1
при r→1
Пусть Т(θ) — непрерывно дифференцируемая 2π-периидичеекая функция. Интегрируя по частям, находим
![]()
Но при любом r< 1
![]()
Правая
часть этого равенства по замечанию,
желанному вначале, стремится к
![]() Итак,
Итак,
![]()
б о
какова
бы ни была 2π-периодическая непрерывно
дифференцируемая функция Т. Пусть
теперь
![]() ,
а
,
а![]() —
равномерно ограниченная последовательность
таких функций, сходящаяся к единице в
(0,θ0)
и к нулю в [0, 2π] \(0,θ0).
Подставляя
Тп
вместо Т
в
последнее равенство и переходя к пределу,
по теореме Лебега получаем
—
равномерно ограниченная последовательность
таких функций, сходящаяся к единице в
(0,θ0)
и к нулю в [0, 2π] \(0,θ0).
Подставляя
Тп
вместо Т
в
последнее равенство и переходя к пределу,
по теореме Лебега получаем
![]()
Следовательно,
![]()
Теорема доказана,
Длина
дуги кривой Г может быть очевидным
образом использована для определения
линейной
меры на
Г. Сначала
пусть
Ơ![]() —
(относительно) открытое подмножество
Г тогда Ơ
есть
счётное объединение попарно Heпepeceкающихся
открытых дуг Ʌk,
и
мы положим |Ơ|=
—
(относительно) открытое подмножество
Г тогда Ơ
есть
счётное объединение попарно Heпepeceкающихся
открытых дуг Ʌk,
и
мы положим |Ơ|=![]() длина Ʌk.
Для
произвольного
подмножества
длина Ʌk.
Для
произвольного
подмножества
![]() определим|E|
как
inf
{|Ơ|:
Ơ
определим|E|
как
inf
{|Ơ|:
Ơ
![]() ,
Ơ
открыто
в Г}. Так как Ф — гомеоморфное отображение
окружности {|z|=
1} на Г, то легко показать, основываясь
на вышеприведенной теореме, что
,
Ơ
открыто
в Г}. Так как Ф — гомеоморфное отображение
окружности {|z|=
1} на Г, то легко показать, основываясь
на вышеприведенной теореме, что
![]()
борелевсках множеств Е на единичной окружности. Имеет место следующий важный результат:
Теорема (Ф. и М. Риссы). Если Е - подмножество единичной окружности и {|z|= 1}, то |Ф(Е)| = 0.
Доказательство.
Пусть
![]() — открытые множества на {|z|=
1},
— открытые множества на {|z|=
1},
![]() такие
что
такие
что![]() Тогда |Ф(Е)|≤|Ф(Ωп)
| для всех n.
Но из предыдущей теоремы н следующего
за ней обсуждения вытекает, что
Тогда |Ф(Е)|≤|Ф(Ωп)
| для всех n.
Но из предыдущей теоремы н следующего
за ней обсуждения вытекает, что
![]()
этот
интеграл стремится к нулю при
![]() так как
так как![]() и
и![]() .
.
