Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке

А. Произведение Бляшке

Если .., и бесконечное произведение

сходится для |z|< 1, то оно представляет некоторую функ­цию, аналитическую в единичном круге; она называется про­изведением Бляшке. Можно даже допустить равенство конечного числа чисел z_n нулю - просто в этом случае множители, соответствующие заменяются на z.

Имеем

откуда

следовательно, рассматриваемое бесконечное произведение сходится при z = 0 тогда в только тогда, когда

Но если , то по той же только что най­денной формуле

при |z|<1; поэтому бесконечное произведение сходится в {\z\ < 1}, если . Таким образом,

сходится в {|z|<1} тогда и только тогда, когда .

2 Граничные значения почти всюду равны по модулю единице

Пусть так что

сходится в {|z|< 1} и представляет функцию В(z), аналитическую в этом круге. Согласно элементарной теории функции комплексной переменной, из того, что каждый сомножитель произведения по модулю меньше 1 в {|z|< 1}, вытекает, что \В(z)\< 1 для |z\< 1.

Следовательно, для почти всех ζ, |ζ|=1, предельная функция B(ζ)=limB(z) при z →ζ существует (теарема Фату).

Теорема. |В(е^iθ)|=1 п. в.

Доказательство.

Без ограничения общности можно счи­тать, что все точки z_n отличны от нуля (в противном случае мы рассмотрели бы функцию B(z)/z^k вместо В (z)). Тогда Теперь из того, что вытекает, что . (NB: для каждогоп. Возьмём число r, 0<r< 1, не равное ни одной из величин |z_n |. Тогда в силу простейшей разновидности фор­мулы Йенсена

,

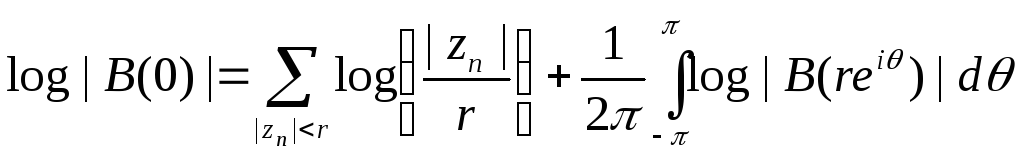т. е.

или

Выберем и зафиксируем какое-нибудь число р, такое что , и возьмёмr< 1 настолько блнзким к 1, чтобы при п=1,2, ,.., р все точки z_n лежали в круге {\z\<r}. Тогда из предыдущего соотношения получим

или, если взять r < 1 достаточно близким к 1,

Это значит, что

поскольку число ɛ>0 было произвольным. Но В (re^iθ) →В (е^iθ) п. в. при r→1, и

Следовательно, по лемме Фату (переходим к пределу по последовательности чисел r, стремящихся к 1)

Поскольку , мы получаем, что

2 Семестр

Лекция 4

Произведение Бляшке. Выделение нулей из класса посредством функции Бляшке.

Возможность построения произведения Бляшке,

имеющего те же нули, что и у заданной функции,

аналитической в единичном круге

Теорема. Пусть функция F(z) регулярна в круге {|z|<1} и z_п — её нули в этом круге, |z_n| < 1. Предположим, что интегралы

ограничены сверху при r< 1. Тогда

так что произведение

сходится в {|z|<1} и имеет место равенство F[z)=b(z) g(z), где функция g(z) регулярна и не имеет нулей в круге {|z|<1}

Доказательство.

Без ограничения общности можно счи­тать, что F(0)≠0; иначе мы рассмотрели бы функцию F(z)/z^k вместо F(z). Тогда если 0<r<1 и не существует точек z_n с |z_n|=r, то по формуле Йенсена

т, е., по предположению,

где М ие зависит от r. Устремляя r к I, получаем, что для любого фиксированного числа р

Следовательно,

Существование произведения Бляшке b(z) доказано ранее. Наконец, определим функцию g(z) в круге {[r]< 1} но формуле g(z)= f(z)/b{z). Вот в всё.

Классы Н^р 0 < р < ∞. Факторизация

Определение Если р > 0, то пространство Н^р состоит нз функций F(z) аналитических в {|z|< 1}, для которых

(1)

Теорема Если р>0, и , то в ζ|<1 имеем

(2)

где b(ζ)—функция Бляшке, a в ζ|<1

Доказательство.

Покажем сначала, что интеграл (6.1) есть неубывающая функция от r в 0<r<1. Действительно, при любом фиксированном ρ, 0 <ρ < 1, функция регулярна ви, следовательно, имеет в ζ|<1 представление:

где

b_ρ(ζ)—функция Бляшке, a в ζ|<1 Функция{h_p(ζ)}^p регулярна в ; следовательно, из примененной к ней формулы

Пуассона имеем в ζ|<1:

Интегрируя это неравенство по Ѳ от 0 до 2π, получаем:

(3)

Но так как в ǀζ|<1 ина ǀζ|=1, тов ǀζ|<1 ина ǀζ|=1, следовательно, имеет место неравенство:

доказанное, таким образом, при любых r и ρ из 0<r<1. Заменяя здесь r на ρ'/ρ, ρ'<ρ, и получим неравенство, доказывающее неубывание интеграла (6.1) в 0<r<1.

Обращаясь теперь к доказательству теоремы, отметим, что в ǀζ|<1 имеет место представление (2) с функцией h(ζ), регулярной и без нулей в ǀζ|<1 . Докажем, что

Пусть верхняя граница интегралов (1) в 0<r<1 равна М.

Обозначив через b_n (ζ) произведение n первых множителей в представлении

(*)

функции Бляшке b (ζ) и выбирая для заданного ε, 0<ε<1, и фиксированного п такое η>0, чтобы в ǀζ|>1-η было ǀb_n (ζ)ǀ > 1- — s, что возможно, при 1 — η <r < 1 имеем:

(4)

Но так как интеграл в (4) есть неубывающая функция от r 0<r<1, то неравенство (4) имеет место и при 0<r<1—η, т. е. во всем промежутке 0<r<1. Фиксируя r и устремляя n k ∞, из (4) получаем при 0<r<1, учитывая еще произвольность ε>0:

Это и доказывает, что и даже более, что верхние границы интегралов (1) дляf(ζ) и для h(ζ) в промежутке 0<r<1 будут равны.

Теорема доказана.

Следствие. Если , то мы можем найти такие две функции g и h, принадлежащие Н ¹ что и не имеющие нулей в {|z|<1}, что

и f=g+h

Замечание. Этот технический результат оказывается часто полезным, так как многие неравенства для функций из Н¹ легче доказывать для функций, не имеющих нулей в {|r|<1}.

Доказательство

Пусть В (r)—произведение Бляшке, построенное по нулям функции f(z). Тогда по предыдущей теореме f= BF, где F(z) не имеет нулей в {|z| < 1}, и

Мы получаем требуемый., результат, полагая

поскольку, как непосредственно проверяется (или же следует из строгого принципа максимума), |В(z)\<1 для |z|< 1.

Следствие. Пусть функция , Тогда её можно предста­вить в виде

где В (z) — произведение Бляшке, а функция g принадлежит H¹ и не имеет нулей в {|z|<1}.

Доказательство.

Функция f(z) допускает представление f=BF, где функция не имеет нулей в {|z|<1}. Положим g(z) = [F(z)]^p для |z|< 1. Тогда функция g(z) одно­значна н регулярна в круге {|z|<1}, поскольку F нигде нём не обращается в нуль.

Лекция 9 - 12