Формула для гармонически спряженной функции

Предположим, что

,

тогда

где, sign 0=0

В самом деле, функция Û(re^iѲ) гармонична в единичном круге, Û(0)=0

Кроме того

аналитическая функция в единичном круге

Теперь, если

где мера на [-π;π], то в вышеприведенном разложении функции U в ряд . Рассматривая разложение в ряд для Û, видим, что

назовем

сопряженным ядром Пуассона. непосредственным суммированием двух геометрических прогрессий найдем, что

Таким образом справедлива теорема

Теорема Если , то гармонически спряженнаяU функция Û задается формулой

Интегральное представление классов

Важную роль в изучении классов играет интегральное представление функций из этих классов.

Сначала докажем следующее утверждение:

Теорема . Пусть где– класс Соболева в. Если при этом существует такое число, чтоипри, то при всехсправедливо представление

(2.5)

где, как обычно,

Доказательство. Пусть фиксировано, положим

Тогда, записав формулу Коши-Грина для функции (см. [31]), имеем:

Используя условие теоремы, получаем:

Упростим подынтегральное выражение:

Следовательно, из равенства (2.5) имеем:

Положив , получаем:

□

Из данной теоремы непосредственно следует:

Теорема Пусть . Тогда еслиилито справедливо представление

Доказательство непосредственно следует из теоремы 2.3, если учесть, что , при этом в условиях теоремыпри.

□

Из интегрального представления классов вытекает:

Теорема. Пространство приотносительно нормы

является банаховым, а при – квазибанаховым пространством.

Доказательство. Пусть . Обозначим черезпространство измеримых в функций , для которых соответствующий интеграл конечен.

Хорошо известно, что пространство прибанахово, а приквазибанахово. Поэтому достаточно установить, чтоявляется замкнутым подпространством пространствапри всех.

Предположим, что – последовательность из, а функциятакая, чтопри .

Докажем, что . Используя оценку (2.1), имеем:

.

Отсюда следует, что последовательность равномерно сходится внутрик некоторой функции. Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательностьтакую, чтопочти всюду в. Поэтомупочти всюду в, и следовательно,. □

Лекция 9

Бесконечные числовые произведения комплексных чисел и их сходимость.

Бесконечное произведение есть выражение вида

(1+а₁)(1+а₂)(1+а₃) .... (1)

содержащее бесконечно много сомножителей. Мы обозначаем его через

Мы предполагаем, что ни одно из чисел а„ не равно —1. Рассмотрим частичное произведение

Мы говорим, что бесконечное произведение (1) сходится, если р_n стремится к некоторому пределу, отличному от нуля, когда п →∞

Мы могли бы, конечно, допустить предел 0, как всякий другой; но мы увидим ниже, что во многих случаях это было бы неудобно.

Если произведение не сходится, то говорят, что оно расхо­дится. Если , то говорят, что оно расходится к нулю.

Мы начнем с рассмотрения двух простых случаев.

Если a_n,≥0 то произведение П(1+a_n) и ряд сходятся или расходятся одновременно.

Так как в этом случае р_n есть неубывающая функция от п, то р_n стремится либо к конечному пределу, либо к положительной бесконечности. Далее,

Левое неравенство становится очевидным, если раскрыть скобки; правое неравенство следует из того, что при любом положительнома. Вместе эти неравенства показывают, что р_n и a₁ +…+a_n ограничены или не ограничены одновременно, и это завершает доказательство.

Если a_n,≤0 для всех значений п, то мы полагаем a_n = -b_n и рассматриваем произведение

Если для всех значений п и рядсходится, то произведениеП(1 — b_п) сходится.

Из сходимости ряда следует существование столь большого N, что b_N + b_N+1+…<1/2 и, в частности, b_n < 1 при n≥N. Оче­видно,

(1 - b_N) (1 - b_N+1)≥1- b_N - b_N+1,

Таким образом, отношение р_п/p_N+1 монотонно убывает при п> N и имеет положительную нижнюю грань. Следовательно, оно стре­мится к положительному пределу. Поскольку , это завер­шает доказательство.

Если 0≤b_n для всех п, но ряд расходится, то про­изведениеП( 1 — b_n) расходится к нулю.

В самом деле, , если 0≤b<1, так что

Правая часть стремится к нулю, что и завершает доказательство.

Таким образом, если если 0≤b_n<1, то произведение П( 1 — b_n) и ряд сходятся или расходятся одновременно.

Общий случай. Пусть теперь a_n — любые вещест­венные или комплексные числа, отличные от —1.

Определение. Произведение П(1+a_n) называется абсолютно сходящимся, если произведение П( 1 — |a_n |) сходится.

Из первого предложения следует, что необходимым и достаточным условием абсолютной сходимости произведения П(1+a_n) служит сходимость ряда

Покажем теперь, что абсолютно сходящееся произведение схо­дится.

Обозначим через р_п то же частичное произведение, что и выше,

и положим Так как

то |р_п — p _n-1|≤|Р_п — Р_п-1|- Если произведение П(1 +|a_n|) схо­дится, то Р„ стремится к некоторому пределу, так что ряд сходится. Тогда, в силу теоремы сравнения, схо­дится и ряд стремится к некоторому пре­делу.

Этот предел не может быть нулем. Действительно, так как ряд сходится и 1+а_п→1, то ряд

также сходится. Следовательно (в силу только что доказанного), произведение

стремится к некоторому пределу.

Но это произведение равно 1/р_п- Следовательно, предел произ­ведения р_п отличен от нуля.

Логарифм бесконечного произведения.

Пусть

верно ли, что

З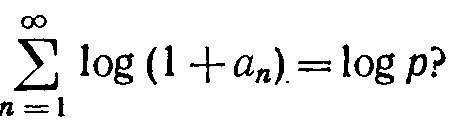десьlog z главное значение логарифма числа z, т. е. значение, мнимая часть которого лежит между —π и π

Ответ будет, очевидно, утвердительным, если все числа а_п действительны и положительны, поскольку тогда все логарифмы имеют свое обычное арифметическое значение. Но в общем случае формула требует модификации.

Пусть р_п обозначает п-е частичное произведение, и пусть , так чтор_п и ρ_n стремятся к пределам и то же отно­сится к аргументу φ_n, если его значения выбраны надлежащим образом. Пусть

тогда, так как а_л →0 при n→∞, то и θ_n →0 Положим

Очевидно,

где k_n — целое число, и 2k_nπ = θ₁ +…+ θ₂ – φ_n. так что

Поскольку правая часть стремится к нулю, при достаточно большом n

и, следовательно, k_n+1 = k_n (напомним, что все k_n — целые числа). Таким образом, k_n имеет при достаточно большом п постоянное значение, скажем k, т. е. Следова­тельно,

Сумма ряда есть, таким образом, некоторое значение, но не обязательно главное значение, логарифма произведения.

Заметим, что в ходе доказательства мы получили для всех достаточно больших значений N равенство

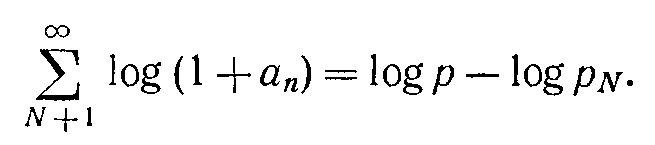
Если мы начнем с ряда логарифмов и положим

то после перехода к экспоненциалам в формуле (1), мы получим равенства

Равномерная сходимость бесконечных произведений.

Бесконечное произведение

где сомножители — функции переменного z, вещественного или комплексного, называется равномерно сходящимся в некоторой области значений z, если частичное произведение

равномерно сходится в этой области к некоторому пределу, нигде не равному нулю.

Вот простейший признак равномерной сходимости произведения.

Произведение

равномерно сходится в каждой области, в которой ряд равномерно сходится к ограни­ченной функции.

Доказательство состоит в пересмотре аргументов ранее доказанной теоремы с точки зрения равномерности. Пусть М — верхняя грань суммы

в рассматриваемой области. Тогда

Полагая

мы видим, что

Следовательно, ряд равномерно сходится, и доказательство завершается так же, как в прошлый раз

Лекция 10