3. Эллипс.

Эллипсом называется множество всех точек, сумма расстояний каждой из которых до двух данных точек F₁ и F₂,называемых фокусами эллипса, есть величина постоянная, равная 2а.

F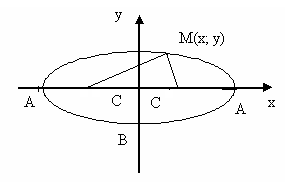₁, F₂ – полюсы эллипса. Расстояние между фокусами обозначим 2с.

Выберем систему координат так, чтобы ось Ох прошла через фокусы и ОF₁=OF₂.

Тогда фокусы имеют координаты F₁(c;0), F₂(-c;0).

Выведем каноническое уравнение эллипса.

По определению эллипса F₁ М + F₂М = 2а.

=2а,

=2а-,

(х+с)²+у²=4а²–4а·+(х-с)²+у²,

х²+2хс+с²+у²-4а²-х²+2хс-с²-у²=-4а²,

4хс-4а² =-4а·, а²-хс=а·,

(а²-хс)²=а²((х–с)²+у²), а⁴–2а²хс+х²с²=а²·(х²-2хс+с²+у²),

а⁴–2а²хс+х²с² –а²х²+2а²хс-а²с²-а²у²=0, х²·(с²–а²)-а²у²=а²·(с²–а²),

х²·(а²–с²)+у²а²=а²·(а²–с²).

Заметим, что а²–с²0, т.к. 2а2с, ас (сумма 2-ух сторон -ка больше его третьей стороны). Обозначим а²–с² =b² , тогда

х²b²+ у²а² =а²b² ,

Разделим на а²b²

(2) += 1 –

каноническое уравнение эллипса.

Так как при замене х на –х, у на –у уравнение не изменится , то эллипс симметричен относительно координатных осей.

Точки пересечения эллипса с осями координат: А, А₁, В, В₁ называются вершинами эллипса. Они имеют координаты А(а; 0), А₁(- а; 0), В(0; b), В₁(0; -b).

а – большая полуось эллипса, b – малая полуось.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине его большой оси, т.е.  =, т.к. с а, то 01.

Если  = 0, то получаем окружность.

Эксцентриситет характеризует степень сжатия эллипса.

²===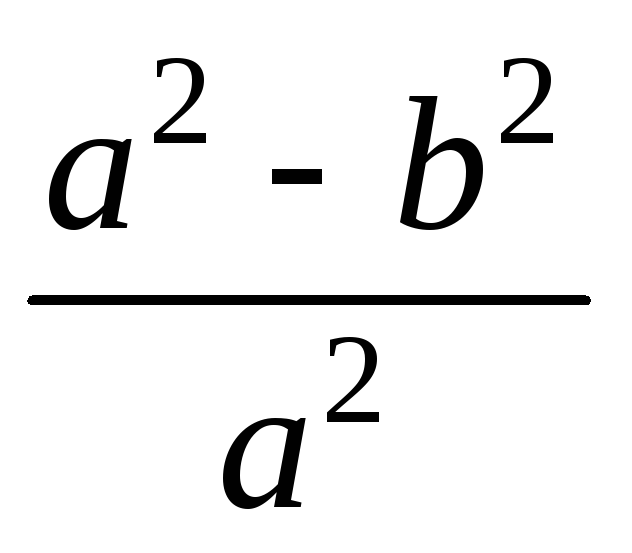1-;=.

Отсюда видно, что, чем больше эксцентриситет, т. е. чем ближе он к 1, тем меньше , и, значит, тем больше вытянут эллипс вдоль оси Ох.

Эксцентриситет , полуоси а и b, расстояние между фокусами 2с – это параметры, которые полностью определяют эллипс с центром в начале координат.

Пример 1.

Найти а,b , с и  эллипса, заданного уравнением:+=4.

Решение.

П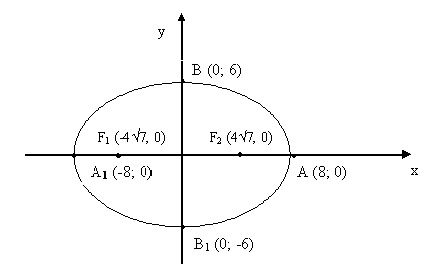риведем уравнение к каноническому виду:

+= 1,+=1.

Отсюда а²=64; а=8,

b²=36, b=6.

a, b, c связаны соотношением а²–с² =b². Значит,

с²=а²–b² =64-36=28, c=.

===1.

3. Гипербола

Гиперболой называется множество всех точек плоскости, разность расстояний каждой из которых до двух данных точек F₁ и F₂ (называемых фокусами гиперболы) величина постоянная, равная 2а.

Обозначим 2с – расстояние между фокусами.

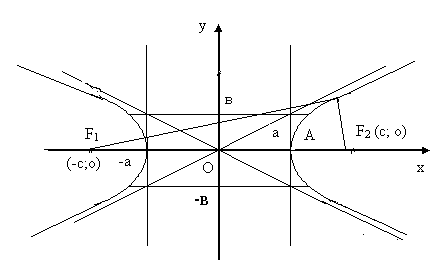
По определению гиперболы: МF₁-МF₂=2а. Вывод уравнения гиперболы аналогичен выводу уравнения эллипса.

(3) =1 –

каноническое уравнение гиперболы, где b²=с²–а². Для гиперболы ас.

а – действительная полуось гиперболы, b – мнимая полуось.

А и A₁ – вершины гиперболы.

Прямоугольник, симметричный относительно О(0;0), со сторонами 2а и 2b, параллельными осям координат, называется основным прямоугольником гиперболы.

Прямые у=х–асимптоты гиперболы.

Эксцентриситетом гиперболы называется отношение  =.

Т.к. с  а, то   1.

²=,=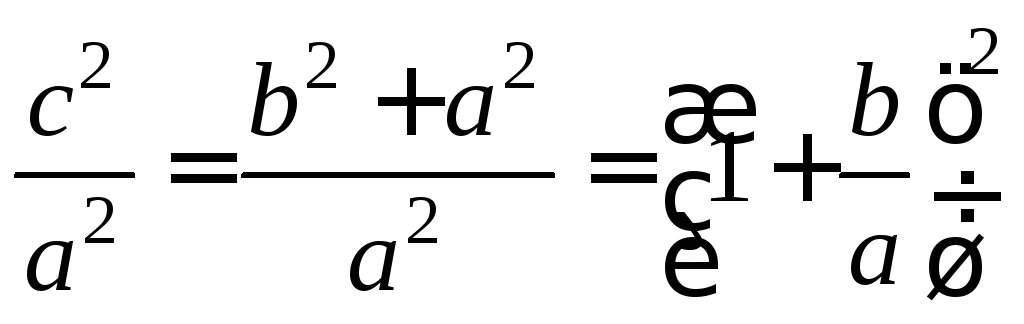

Чем меньше эксцентриситет гиперболы, т.е. он ближе к 1, тем больше вытянут основной прямоугольник по оси Ох

Если у гиперболы а=b, то гипербола называется равносторонней. Её уравнение: х²-у²=а².

Прямые у=x вляются её асимптотами.

Пример 2

Н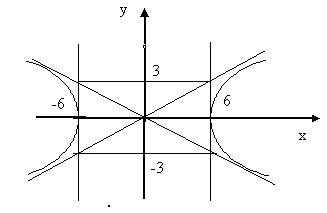айти а, в, с и гиперболы, заданной уравнением х²-4у²=36.

Решение.

Приведем данное уравнение к каноническому виду: .

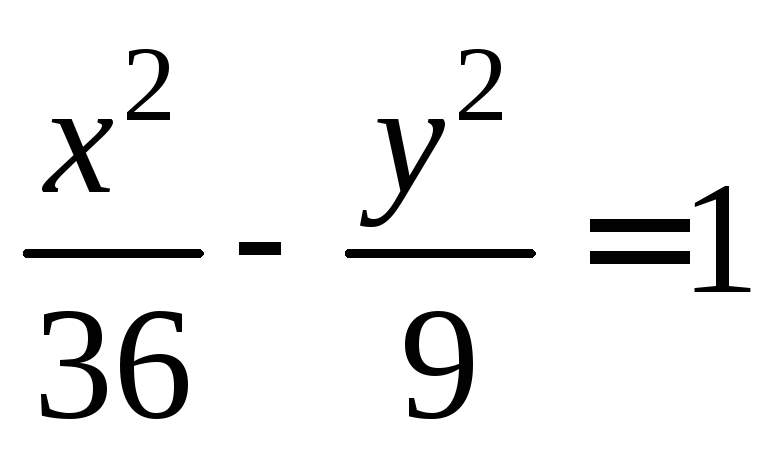Отсюда ясно, что а²=36, а=6,

b²=9, b=3.

с²=а²+b²=36+9=45; с=,

 =; ==1.