4. Непрерывность сложной функции

Пусть функция t=g(x) определена на D(g), а функция y=f(t) определена на D(f), и xD(g) t=g(x)D(f). Тогда на D(g) определена сложная функция y=h(x)=f(g(x)).

Теорема 3. Если функция t=g(x) непрерывна в точке x₀D(g) , а функция y=f(t) непрерывна в точке , то сложная функцияf(g(x)) непрерывна в точке x₀, т.е. . (6)

Доказательство следует из определения непрерывности функции в точке и теоремы о пределе сложной функции.

Замечание. Так как , то из (6) следует

(7)

т.е. операция предела переставима с операцией вычисления непрерывной функции. Причем (7) выполняется и в том случае когда g(x) не является непрерывной в точке x₀.

Следствие. Если функция t=g(x) непрерывна на D(g), а y=f(t) непрерывна на D(f), то сложная функция y=f(g(x)) непрерывна на D(g).

Пример.

а) Доказать, что непрерывна на.

 I способ.

Данная функция сложная: . Функциянепрерывна на,непрерывна на непрерывна на.

II способ.

. Значит, функция непрерывна в  непрерывна на .

б) Исследовать на непрерывность функцию .

 определена и непрерывна в любой точке , определена и непрерывна на , значит,определена и непрерывна. Значит, непрерывна на.

5. Применение непрерывности функций при вычислении пределов

Пример 1. Доказать .

 

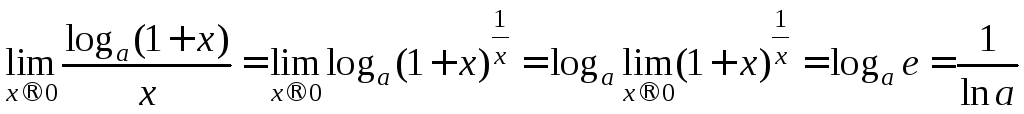
Частный случай .

Пример 2. Доказать .

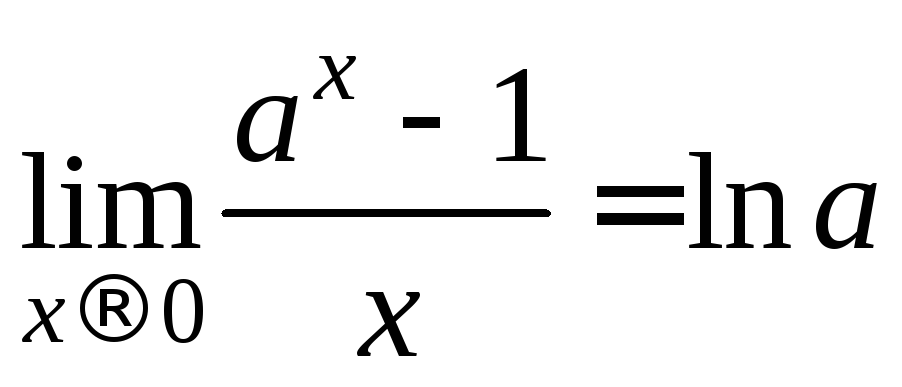 Введем новую переменную . Тогда

. 

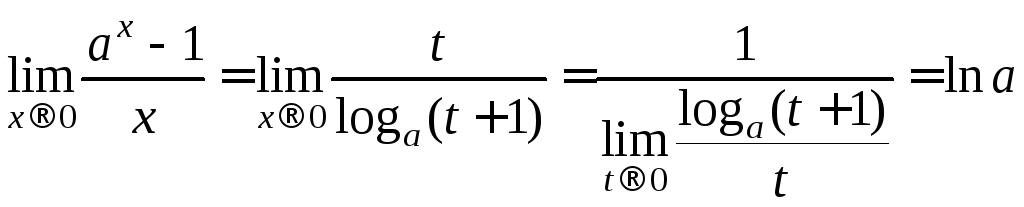Частный случай .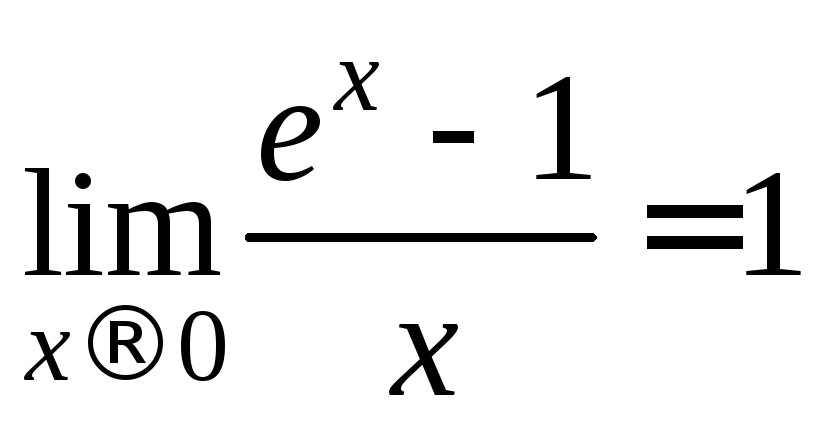

Пример 3. Доказать .

. 

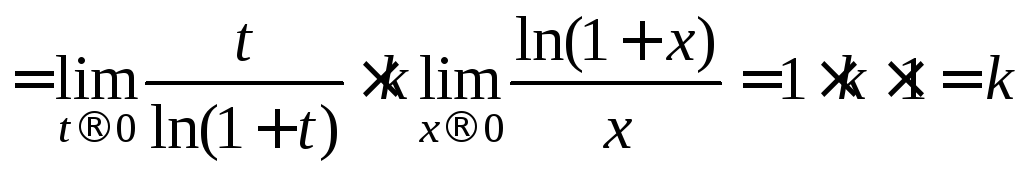Пример 4.  .

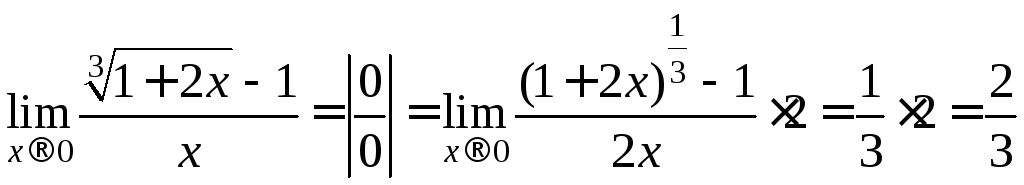§22. Точки разрыва и их классификация

Согласно определению 1 функция f(x)непрерывна в точке x₀, если

(1)

Очевидно, что условие (1) предполагает выполнение одновременно следующих условий:

1) , т.е.;

2) ;

3) .

Если в точке x₀ хотя бы одно из условий не выполняется, то не выполняется (1), следовательно, в точке x₀ функция является разрывной, значит, x₀ - точка разрыва функции f(x).

Определение 1. Точка x₀ разрыва функции f(x) называется точкой разрыва I рода, если в этой точке существуют конечные односторонние пределы f(x₀-0), f(x₀+0).

Величина называетсяскачком функции в точке x₀.

Пример 1. Исследовать на непрерывность функцию

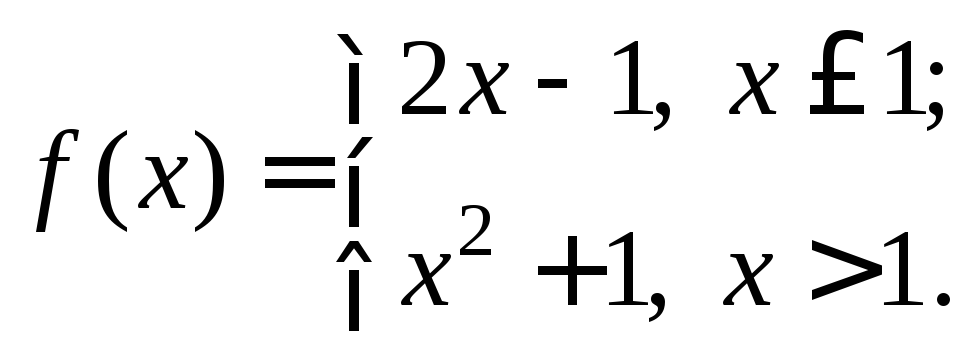
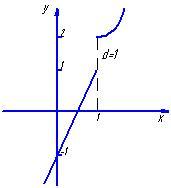 Функция непрерывна на, в том числе на. Функциянепрерывна на, в том числе на. Исследуем на разрыв точкух=1.

. Следовательно, х=1 - точка разрыва I рода.

. 

Определение 2. Точка x₀ разрыва функции f(x) называется точкой устранимого разрыва, если , т.е.(но либо, либо).

Если x₀ - точка устранимого разрыва, то разрыв можно устранить, если доопределить или переопределить функцию в точке x₀, положив . Тогда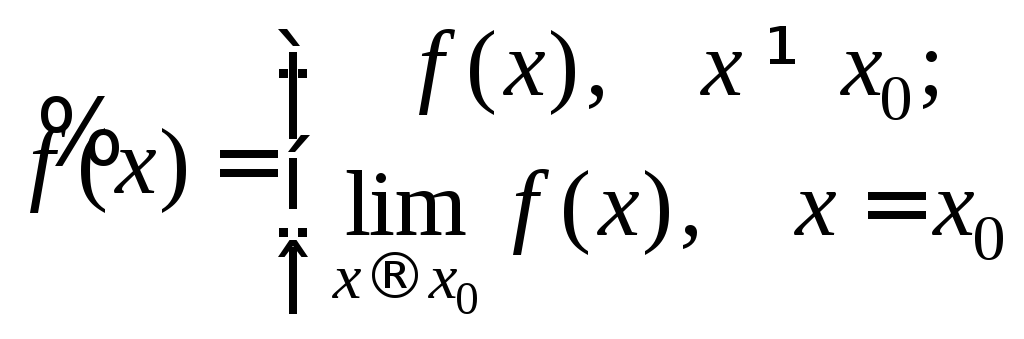непрерывна в точкеx₀.

Пример 2. Исследовать на непрерывность функцию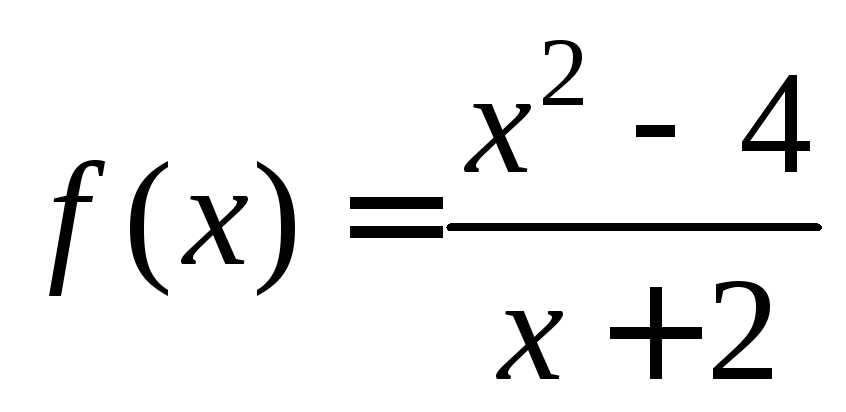

.

Функция является непрерывной на D(f) (отношение двух многочленов). Исследуем точку х=-2.

.

Значит, х=-2 - точка устранимого разрыва.

Доопределим функцию в точке х=-2:

.

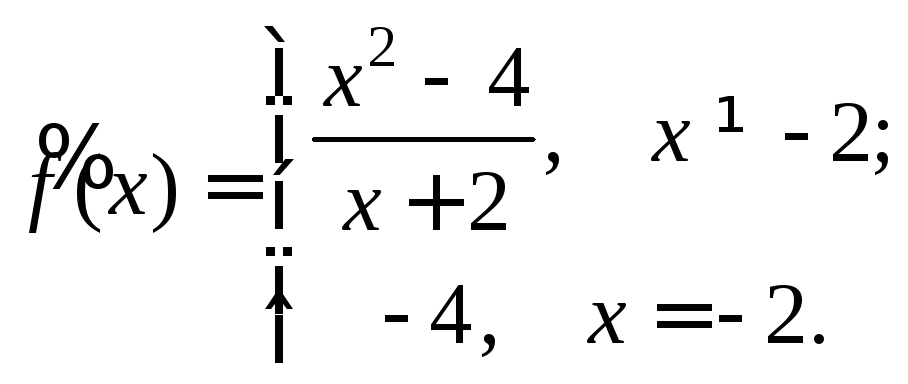непрерывна в точке х=-2. 

Определение 3. Точка x₀ разрыва функции f(x) называется точкой разрыва II рода, если в точке x₀ не существует или равен бесконечности хотя бы один из односторонних пределов.

Пример 3. Исследовать на непрерывность

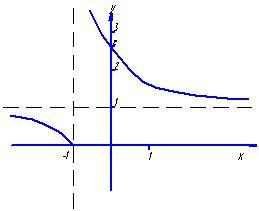
 функция непрерывна на D(f) (композиция непрерывных функций), исследуем точку x=-1.

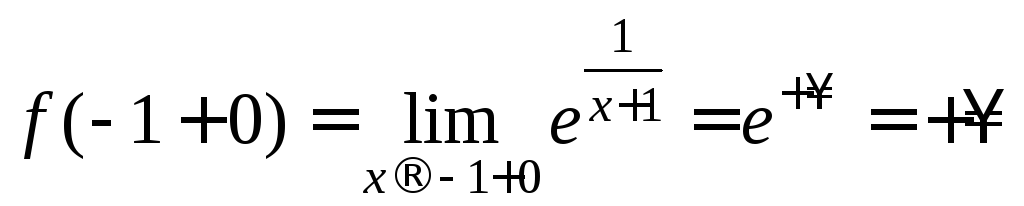, . Следовательно,x=-1 - точка разрыва второго рода ().