
- •§ 21. Непрерывность функции
- •1. Основные определения.
- •4. Непрерывность сложной функции
- •5. Применение непрерывности функций при вычислении пределов
- •§22. Точки разрыва и их классификация
- •§23. Свойства непрерывных функций
- •1. Свойства функций, непрерывных в точке
- •2. Свойства функций, непрерывных на промежутке
- •§24. Непрерывность обратной функции
- •§25. Непрерывность элементарных функций
- •1. Определение элементарной функции.
- •2. Степенная функция.
- •3. Показательно- степенная функция
- •4. Гиперболические функции
- •5.Обратные тригонометрические функции
- •§26. Равномерная непрерывность функций
3. Показательно- степенная функция
Показательно-степенной
функцией
называется функция вида
![]() ,
она определена
,
она определена![]() .
.
По
свойству логарифма можно записать:
![]() ,
тогда
,
тогда
![]() . (1)
. (1)
Рассмотрим
композицию функций:
![]() .
Если
.
Если![]() и
и![]() непрерывны, то в силу непрерывности
логарифма и показательной функции (1)
непрерывна.
непрерывны, то в силу непрерывности
логарифма и показательной функции (1)
непрерывна.
1)
Пусть
![]() ,
,![]() ,А
и В
- числа.
,А
и В
- числа.
Выясним,
чему равен
![]()
![]() .
.
![]() .
.
В силу непрерывности показательной функции
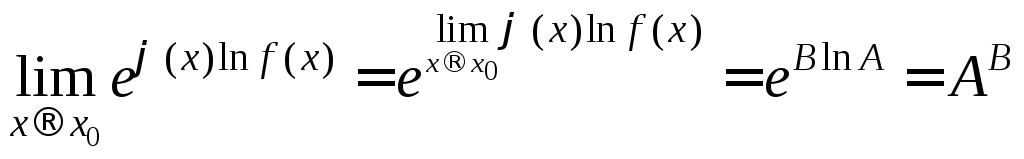 . (2)
. (2)
В
(2)
![]() может быть числом,
может быть числом,![]() ,
либо можно рассматривать односторонние
пределы.
,
либо можно рассматривать односторонние
пределы.
Из
(2) следует
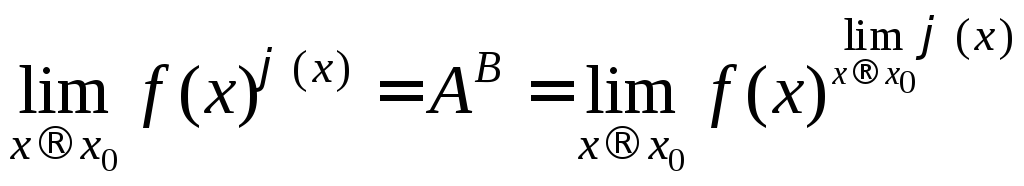 .
.
2)
Но
![]() является неопределенностью
является неопределенностью![]() в следующих случаях:
в следующих случаях:
а)
B=0,
lnA=+
A=+,
тогда
![]() ;
;
б)
B=0,
lnA=-
A=0,
тогда
![]() ;
;
в)
B=,
lnA=0
A=1,
тогда
![]() .
.
Пример.
а)
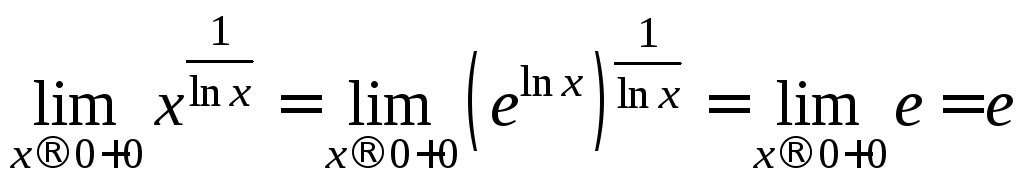 ;
;
б)
![]() .
.
4. Гиперболические функции
Частным
случаем показательной функции
![]() является
является![]() .
Черезex
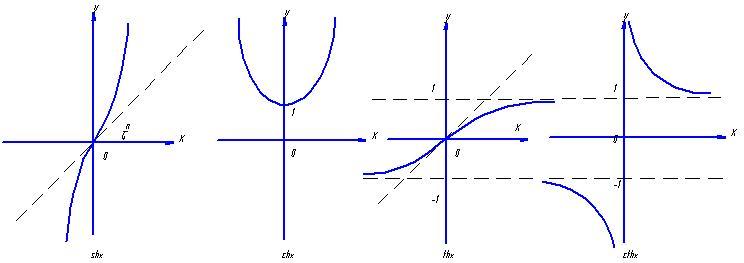
определяются гиперболические функции:
.
Черезex
определяются гиперболические функции:
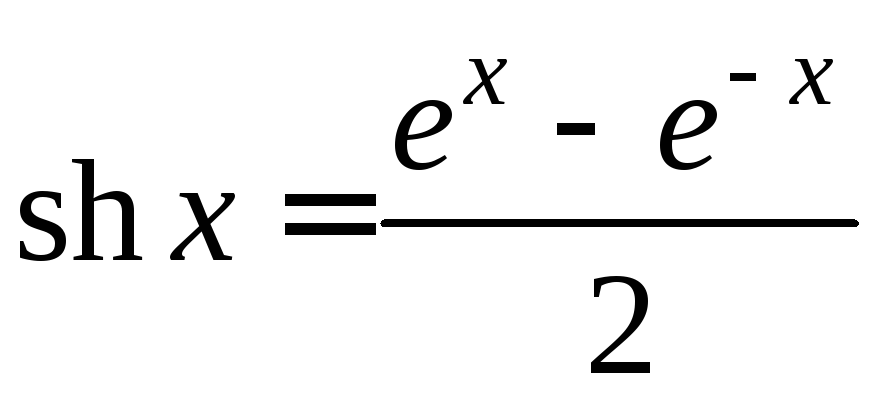 -
гиперболический синус;
-
гиперболический синус;
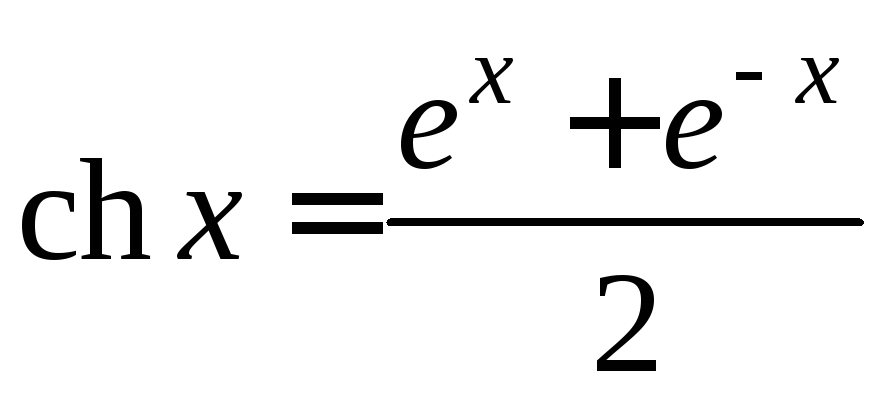 -
гиперболический косинус;
-
гиперболический косинус;
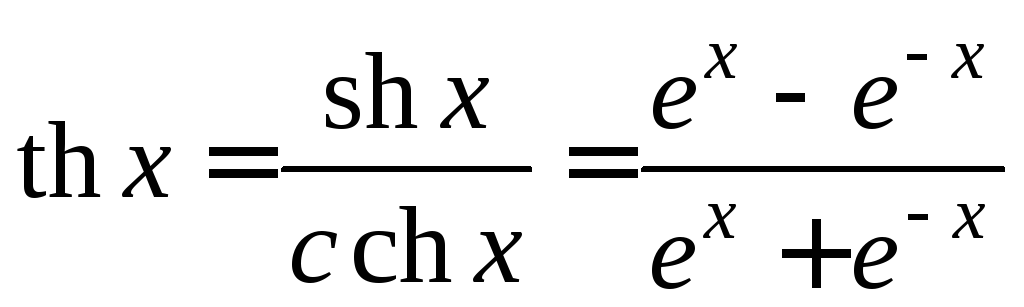 -
гиперболический тангенс;
-
гиперболический тангенс;
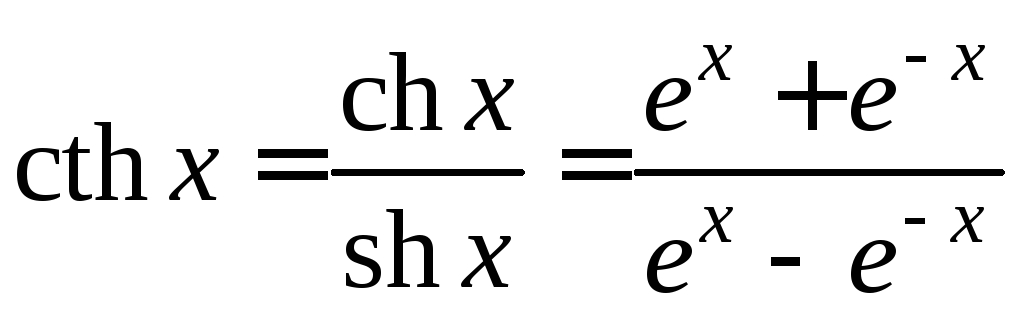 -
гиперболический котангенс.
-
гиперболический котангенс.
Все
гиперболические функции являются
элементарными, так как являются
результатом арифметических операций
над показательными функциями ex
и e-x.
Следовательно, они являются непрерывными
в своих областях определения. Название
"гиперболические" они получили
потому, что
![]() удовлетворяют уравнению гиперболы
удовлетворяют уравнению гиперболы![]() ,
подобно тому, как тригонометрические
функцииX=cosx,
Y=sinx
называют "круговыми" , т.к.
удовлетворяют уравнению окружности
,
подобно тому, как тригонометрические
функцииX=cosx,
Y=sinx
называют "круговыми" , т.к.
удовлетворяют уравнению окружности
![]() .
Названия гиперболический синус, косинус,
тангенс, котангенс происходит от того,
что между ними имеют место соотношения,
напоминающие или совпадающие ссоответствующими
соотношениями между тригонометрическими
функциями.
.
Названия гиперболический синус, косинус,
тангенс, котангенс происходит от того,
что между ними имеют место соотношения,
напоминающие или совпадающие ссоответствующими
соотношениями между тригонометрическими
функциями.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
s hx,
chx,
thx
определены на
hx,
chx,
thx
определены на
![]() ,cthx
определена на
,cthx
определена на
![]() .
.
5.Обратные тригонометрические функции
1 .
Рассмотрим
.
Рассмотрим![]() на
на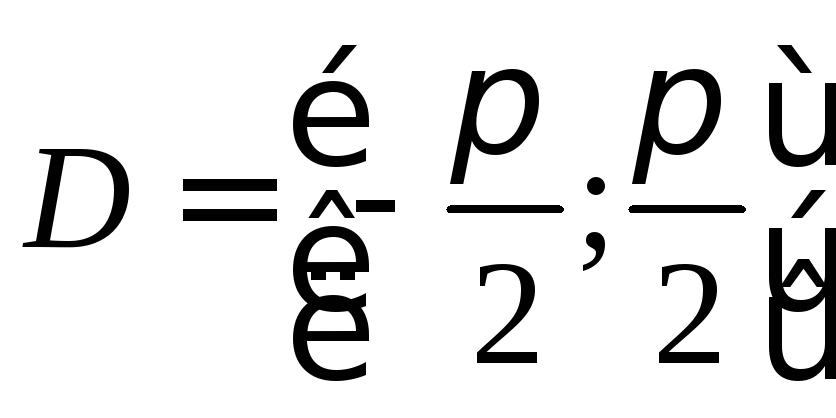 -возрастает
и непрерывна наD(f),
E(f)=[-1;1].
Значит, эта она имеет обратную функцию,
определенную, возрастающую и непрерывную
на [-1;1]. Эта функция обозначается
-возрастает
и непрерывна наD(f),
E(f)=[-1;1].
Значит, эта она имеет обратную функцию,
определенную, возрастающую и непрерывную
на [-1;1]. Эта функция обозначается ![]() ,
D(arcsinx)=[-1;1],
,
D(arcsinx)=[-1;1],
 .
.
Arcsinx
- это такой угол из
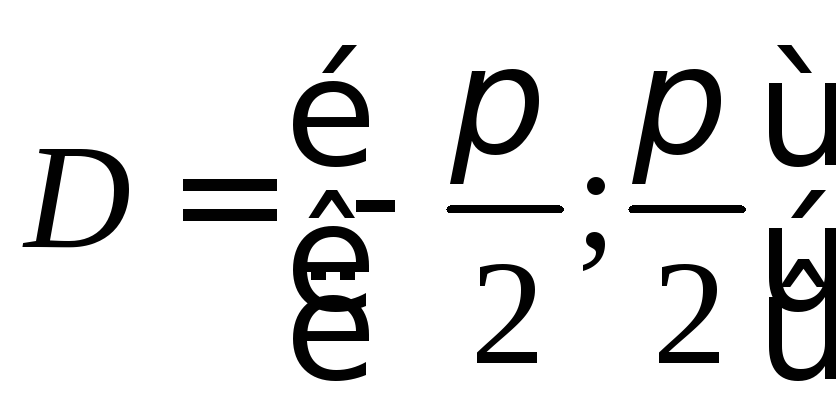 ,
синус которого равенx.
,
синус которого равенx.
2. Рассмотрим f(x)=cosx на D=[0;] - непрерывна и убывает, E(f)=[-1;1]. Следовательно, существует обратная функция, определенная, непрерывная и убывающая на [-1;1]. Она обозначается y=arccosx, D(arccosx)=[-1;1], E(arccosx)=[0;]. Arccosx - это такой угол из [0;], косинус которого равен х.
3
 .Рассмотримf(x)=tgx
на
.Рассмотримf(x)=tgx
на
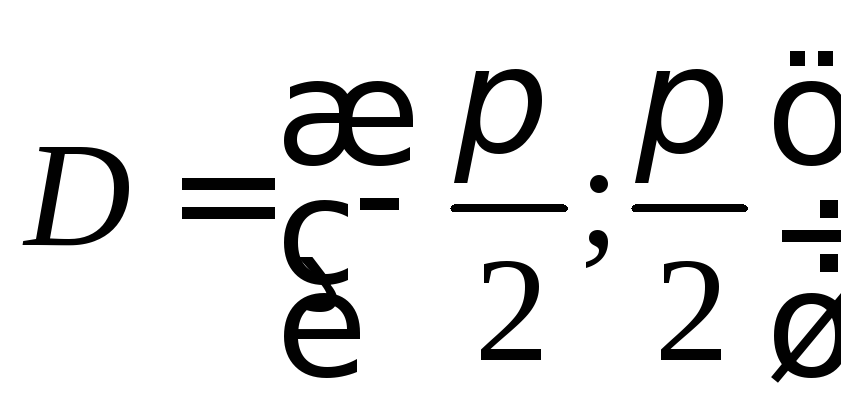 - непрерывна и возрастает,
- непрерывна и возрастает,![]() .
Следовательно, существует обратная
функция, определенная, непрерывная и
возрастающая на
.
Следовательно, существует обратная
функция, определенная, непрерывная и
возрастающая на![]() .
Обозначается y=arctgx,
D(arctgx)=
.
Обозначается y=arctgx,
D(arctgx)=![]()
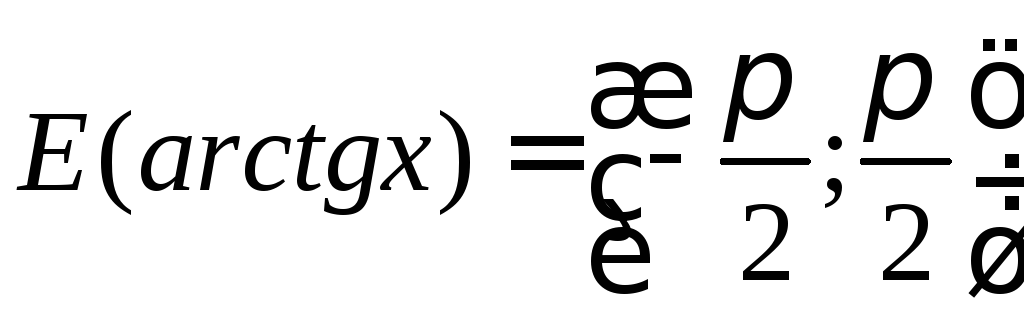 .
Arctgx
- это такой угол из
.
Arctgx
- это такой угол из  ,
тангенс которого равен х.
,
тангенс которого равен х.
4.
Рассмотрим f(x)=сtgx
на
![]() - непрерывна и убывает,
- непрерывна и убывает,![]() .
Значит, существует обратная функция,
определенная, непрерывная и убывающая
на
.
Значит, существует обратная функция,
определенная, непрерывная и убывающая
на
![]() .
Обозначается y=arсctgx,
D(arсctgx)=
.
Обозначается y=arсctgx,
D(arсctgx)=![]() ,
,
![]()
![]() .
Arctgx
- это такой угол из
.
Arctgx
- это такой угол из ![]() ,
котангенс которого равен х.
,
котангенс которого равен х.
Имеют место тождества:
![]() ,
,
![]() .
.
§26. Равномерная непрерывность функций
Понятие непрерывности функции относится к отдельно взятой точке, т.е. является свойством функции в точке. Непрерывность функции f на <a;b> определяется как ее непрерывность в каждой точке этого промежутка.
f(x)
непрерывна в т. x0
![]() .
.
Можно
доказать, что
![]() (на примере
(на примере![]() )
)
Проблема:
возможна ли ситуация, чтобы
не зависело от x0,
где x0
меняется на <a;b>,
т.е. чтобы
![]()
Определение
1.
f(x)
называется равномерно
непрерывной на промежутке
<a;b>,
если
![]()
![]() .
.
Определение
2.
f(x)
не является равномерно непрерывной на
<a;b>
если
![]()
![]()
Теорема 1. Если f(x) равномерно непрерывна на <a;b>, то она непрерывна на < a;b>.
Доказательство.
![]() Возьмем
Возьмем
![]() .По
условию для выбранного
.По
условию для выбранного
![]()
![]() .
.
Пусть
x2=x0,
x1=x.
Тогда
![]() выполнено
выполнено![]() .
Значит (по определению) функция непрерывна
в точкеx0,
а так как она произвольно взята из
промежутка <a;b>,
то функция непрерывна на всем промежутке.
.
Значит (по определению) функция непрерывна
в точкеx0,
а так как она произвольно взята из
промежутка <a;b>,
то функция непрерывна на всем промежутке.
![]()
Замечание. Обратное утверждение не верно.
Пример.
![]() непрерывна на (0;1). Докажем, что она не
является равномерно непрерывной на
(0;1).
непрерывна на (0;1). Докажем, что она не
является равномерно непрерывной на
(0;1).
Пусть
![]() .
Выберем
.
Выберем![]() .
Найдем
.
Найдем ![]() ,
а
,
а
![]() .
Возьмемх2(0;1),
а
.
Возьмемх2(0;1),
а
![]() .
Тогда
.
Тогда![]() ,
,
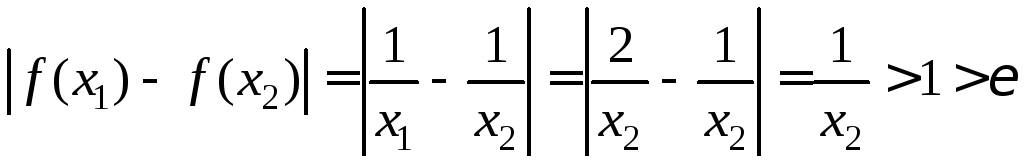 .
.
По определению 2 функция не является равномерно непрерывной на (0;1).
Теорема 2. (Кантора) Если f(x) непрерывна на отрезке [a;b], то она равномерно непрерывна на [a;b].
Доказательство.
![]() (От
противного) Пусть f(x)
не является равномерно непрерывной на
[a;b],
тогда по определению 2
(От
противного) Пусть f(x)
не является равномерно непрерывной на
[a;b],
тогда по определению 2
![]()
![]() .
.
Возьмем
последовательность положительных чисел
![]() :
:![]() .
.
Для
![]() найдутся
такие точки
найдутся
такие точки![]() [a;b],
такие, что
[a;b],
такие, что
![]() ,
но
,
но![]() .
.
Для
![]()
![]() [a;b]:
[a;b]:
![]() ,
но
,
но
![]() .
.
Для
![]()
![]() [a;b]:
[a;b]:
![]() ,
но
,
но
![]() .
.
. . . . . . . . . . . . . . . .
Для
![]()
![]() [a;b]:
[a;b]:
![]() ,
но
,
но
![]() .
.
. . . . . . . . . . . . . . .
Этот процесс продолжаем бесконечно. В результате из [a;b] выделится 2 ограниченные последовательности
![]() :
:
![]()
![]() :
:
![]()
Из
последовательности
![]() по т. Больцано-Вейерштрасса можно
выделить сходящуюся подпоследовательность
по т. Больцано-Вейерштрасса можно
выделить сходящуюся подпоследовательность
![]() .
Пусть
.
Пусть
![]() .Покажем,
что и
.Покажем,
что и
![]() сходится к точке x0.
сходится к точке x0.
![]() .
.
Так
как
![]() ,
то
,
то![]()
![]()
![]() .
.
Выберем
![]() .
.
Тогда,
т.к.
![]() ,
то из (1) и (2)
для выбранного
,
то из (1) и (2)
для выбранного
![]()
![]() .
.
По
условию f(x)
непрерывна на отрезке [a;b],
следовательно, она непрерывна в точке
x0[a;b].
Тогда по определению предела функции
по Гейне для последовательностей
![]() и
и![]() соответствующие и последовательности
значений функции
соответствующие и последовательности
значений функции![]() и
и![]() должны сходиться кf(x0),
тогда
должны сходиться кf(x0),
тогда
![]() при
при![]() ,
но это противоречит тому что
,
но это противоречит тому что
![]()
![]() (а, следовательно, и
(а, следовательно, и
![]()
![]() ).
).![]()
